Ondes, oscillateur, plan incliné. Concours orthoptie.

Ondes, oscillateur, plan incliné. Concours orthoptie.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Exercice 1.
1. Les ondes sonores audibles par l'oreille humaine ont une fréquence comprise entre 20 Hz et 20 kHz. Entre quelles valeurs sont comprises les longueurs d'onde correspondantes, si la célérité du son dans l'air vaut 340 m/s ?
l = v / f ; 340 / 20 = 17 m ; 340 / (2,0 10⁴) =0,017 m.
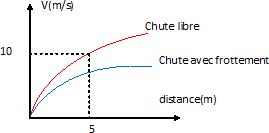
2. On laisse tomber un objet du haut d'une tour. Faites un graphique ( pour chaque cas ) représentant le module de la vitesse en fonction de la distance parcourue depuis le début de la chute, lorsque la résistance de l'air est négligeable, prise en compte.

3. On considère deux situations :
Un sprinter évoluant à une vitesse de 10 m/s dans un référentiel terrestre et les protons éjectés par le quasar à 200 000 km/s dans le référentiel galiléen du quasar. Calculer le facteur de Lorentz correspondant à chaque vitesse.
Sprinter : ß² = [v / c ]²= [10 / (3,0 10⁸) ]²=1,1 10^-15 ; g = (1-ß²)^-½ =(1-1,1 10^-15 )^-½~1,0.
Quasar : ß² = [v / c ]²= [2,0 10⁸ / (3,0 10⁸) ]²=0,444 ; g = (1-ß²)^-½ =(1-0,444 )^-½~1,34.

4. Convertir 11011 ( écrit en base 2) en base 10.
1*2⁰ +1*2 +0*2²+1*2³*1*2⁴ s'écrit 27 en base 10.
Ecrire 78 ( écrit en base 10) en base 2.
78 = 1*2⁶ +0*2⁵+0*24 +1*2³+1*2²+1*2+0*2⁰ s'écrit 1001110 en base 2.

5. Pour contrôler la vitesse d'une voiture sur autoroute, un radar Doppler de police émet des ondes électromagnétiques, appelées " ondes centimétriques" de fréquence 24,125 GHz.. Justifier cette dénomination.
l = c / f = 3,0 10⁸ / (24,125 10⁹) ~0,012 m =1,2 cm.
La longueur d'onde est de l'ordre du centimètre.

.
.

Exercice 2. Surfer sur la vague..
La houle est un train de vagues régulier générée par un vent soufflant sur une grande étendue d'eau sans obstacle, le fetch. En arrivant près du rivage, sous certaines conditions, la houle déferle au grand bonheur des surfeurs.
1. De quel type d'onde est la houle ? Justifier.
La houle est une onde mécanique profgressive transversale.
La houle correspond à la propagation d'une perturbation dans un milieu matériel, sans transport de matière, mais avec transport d'énergie.
Il est possible de simuler la houle au laboratoire de physique avec une cuve à ondes en utilisant une lame vibrante qui crée à la surface de l'eau une onde progressive sinusoïdale de fréquence f = 23 Hz. On réalise une photographie du phénomène observé. En réalisant une photographie du phénomène observé, on mesure 10 longueurs d'onde sur une distance de 14 cm.
2. Déterminer la vitesse de propagation v de l'onde sinusoïdale générée.
v = l f = 1,4 10^-2 *23 =0,327 ~0,33 m/s.
Au large de la pointe bretonne, à une profondeur de 3000 m, la houle s'est formée avec une longueur d'onde de 60 m.
Vitesse de propagation des ondes à la surface de l'eau ( en eau profonde) : v = (gl /(2p))^½.
3. Calculer la vitesse v₁ de propagation de cette houle et en déduire sa période T.
v₁ = (9,8*60 / 6,28)^½ =9,674 ~9,7 m/s.
T = l / v₁ = 60 / 9,674 =6,2 s.
La houle atteint une côte sablonneuse et rentre dans la catégorie des ondes longues.
4. Calculer la vitesse de propagation v₂ de la houle pour une profondeur h = 4,0 m ainsi que sa nouvelle longueur d'onde. Que remarque t-on lorsque l'onde atteint des eaux peu profondes ?
v₂ = (gh)^½ = (9,8*4,0)^½ =6,26 ~6,3 m/s.
La fréquence ( donc la période) restant constante, l = v₂ T= 6,26 * 6,20 =38,8 ~39 m.
En atteignant des eaux peu profondes, la longueur d'onde diminue.
Un autre phénomène très attendu par les surfeurs, lors des marées importantes est le mascaret.
Le mascaret est une onde de marée qui remonte un fleuve. Cette onde se propage à une vitesse v de l'ordre de 5,1 m/s. Le passage du mascaret étant observé sur la commune d'Arcins à 17 h 58.
5. A quelle heure arrivera-t-il à un endroit situé à une distance de 13 km en amont du fleuve ?
13 10³ / 5,1 =2,55 10³ s ou 42,48 min soit 42 min 29 s.17 h 58 + 42 min = 18 h 40 min.

Exercice 3. Vrai ou Faux, justifier.
A. On donne le graphe représentant l'énergie cinétique et l'énergie potentielle élastique d'un système ( solide ressort ) horizontal en fonction du temps. La masse m est écartée de sa position d'équilibre d'une valeur x₀ et lâchée sans vitesse initiale à l'instant t=0. L'origine des abscisses correspond à la position d'équilibre du système.
Affirmation 1. La courbe en trait plein correspond à l'énergie cinétique.

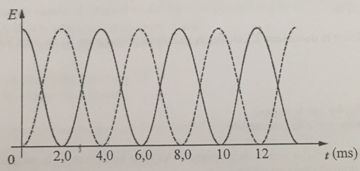
Faux, la vitesse initiale, donc l'énergie cinétique, est nulle.
Le système comporte un ressort de raideur k et une masse m. On suppose que l'énergie potentielle de pesanteur est nulle au niveau horizontal où se situe le système.
Affirmation 2. L'expression de l'énergie mécanique est E_m = ½kx₀². Vrai.
L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle.
L'énergie mécanique est constante ( l'amplitude des courbes ne diminue pas )
Initialement l'énergie mécanique est sous forme potentielle élastique.
Affirmation 3. L'allure des courbes permet d'affirmer que les frottements sont négligeables. Vrai.
L'amplitude des courbes ne diminue pas au cours du temps.
Affirmation 4. La période propre du système est T = 4,0 s. Faux.
La période des courbes ci-dessus est de 4,0 s. La période de ½kx₀² est de 4,0 s ; la période de x(t) est donc de 8,0 s.
Affirmation 5. La période propre du système est doublée si la masse est multipliée par 2. Faux.
T = 2 p |m/k]^½. Pour que la période double, il faut que la masse quadruple, k restant constant.

B. A l'aide d'un microphone et d'un dispositif d'acquisition de données relié à un ordinateur, on réalise les enregistrements de notes jouées par divers instruments puis on réalise les spectres de fréquences.

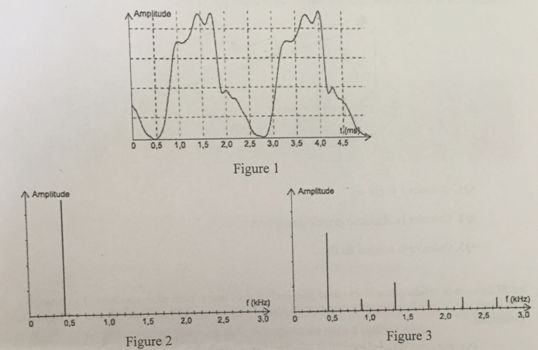
Afirmation 6. Le spectre de la figure 1 correspond à l'enregistrement de la figure 2. Faux.
Figure 1 : le son est complexe, la courbe n'est pas une sinusoïde ; figure 2 : le son est pur ( pas d'harmonique).
Afirmation 7. Les spectres des figures 2 et 3 correspondent à des sons de même hauteur. Vrai.
La fréquence du fondamental ( harmonique de rang 1 ) est la même.
Afirmation 8. Les spectres des figures 2 et 3 correspondent à des sons de même timbre. Faux.
Ces deux sons ne possèdent pas les mêmes harmoniques.
Afirmation 9. Quand l'intensité sonore I est triplée, le niveau sonore L augmente de 4,8 dB. Vrai.
Le niveau sonore augmente de 10 log 3~4,8 dB.
Afirmation 10. Le niveau sonore mesuré est indépendant de la distance entre le microphone et les instruments. Faux.
L'intensité sonore diminue avec la distance microphone- instruments.

Exercice 4. Plan incliné.
Soit un solide de masse m = 100 g en équilibre suspendu par un fil inextensible et sans raideur sur un plan incliné : L = 400 mm et hauteur maximale du plan h = 1,9 dm. On prend g = 10 m s^-2.
1. Calculer l'angle a, inclinaison du plan par rapport à l'horizontale.
sin a = h / L = 0,19 / 0,400 = 0,475 ; a = 28,36 ~28°.
2. Calculer la réaction normale du support.

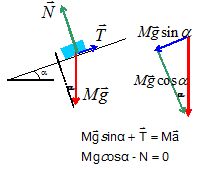
N = Mg cos a =0,100 *10 cos 28,36 = 0,88 N.
3. Calculer la tension du fil.
T = Mg sin a =0,100 *10 sin 28,36 =0,475 ~ 0,48 N.
Le fil casse et le solide glisse alors sur le plan incliné avec une accélération constante. La distance parcourue par le mobile pour arriver en bas du plan est de d=0,25 m. On néglige les forces de frottement.
4. Calculer le travail du poids lors du déplacement.
Travail moteur en descente. W = +Mg d sin a = 0,100 *10 sin 28,36 *0,25 =0,1188 ~0,12 J.
5. Le travail de la réaction du plan incliné est-il moteur, résistant ? Justifier.
La réaction du plan est perpendiculaire au déplacement : son travail est donc nul.
6. Calculer la vitesse acquise par le solide après ce déplacement de 0,25 m.
Théorème de l'énergie cinétique ( seul le poids travaille et la vitesse initiale est nulle).
½mv² = 0,1188 ; v² = 0,1188 *2 / 0,100 = 2,375 ; v = 1,541 ~1,5 m /s.
7. Calculer l'accélération du mobile.
a = g sin a = 10 *0,475 = 4,75 ~4,8 m s^-2.

menu