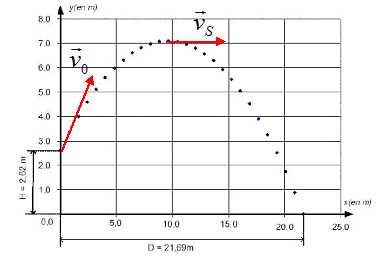
Lancer du poids. Concours orthoptie Nantes 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Le vainqueur de l'épreuve de lancer du poids a réussi un jet à une distance D = 21,69 m. Pour simplifier, on ne travaillera que sur le centre d'inertie du boulet ( nom courant donné au poids ). L'entraîneur de l'un des concurrents souhaite étudier ce lancer. Oldispose de la vitesse initiale v0 du centre d'inertie du boulet mesurée à l'aide d'un cinémomètre et de l'altitude h. v0 = 13,7 m/s ; h = 2,75 m ; g = 9,81 m s-2. Un logiciel informatique lui permet de réaliser une simulation de ce lancer et de déterminer la valeur de l'angle du vecteur vitesse initiale avec l'horizontale soit a = 43°.   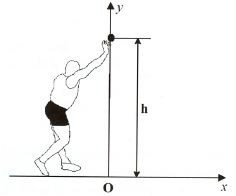Pour chacun des graphes suivants, les dates correspondant à deux points successifs sont séparées par le même intervalle de temps. 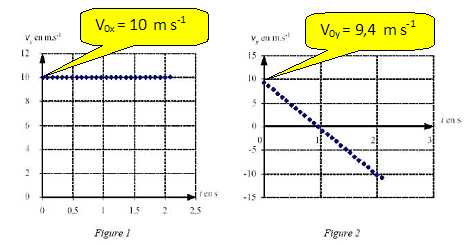1. Etude des résultats de la simulation. 1.1 Etude des conditions initiales du lancer. a. Déterminer les composantes vox et voy du vecteur vitesse à l'instant de date t=0. v0x = 10 m s-1 ; v0y = -9,8 m s-1. b. Vérifier que la valeur de la vitesse instantanée et l'angle de tir sont compatibles avec les valeurs respectives v0 = 13,7 m/s et a = 43°données. v0 =[v0x2 +v0y2]½ =102 +(-9,8)2]½ =14 m s-1 ( écart 2 % par rapport à la valeur donnée ). tan a = |v0y|/ v0x =9,8 / 10 = 0,98 ; a = 44°. ( écart 2 % par rapport à la valeur donnée ). . . 1.2. Etude du vecteur vitesse du centre d'inertie du boulet. a. Déterminer toutes les caractéristiques du vecteur vitesse du centre d'inertie du boulet au sommet de la trajectoire. Au sommet de la trajectoire la composante verticale v0y de la vitesse est nulle. vS = v0x = 10 m s-1. b. Sur le graphe y = f(x) tracer les vecteurs vitesses v0 et vS. 2. Etude théorique du mouvement du centre d'inertie. 2.1. Par application de la seconde loi de Newton, dans le référentiel terestre supposé galiléen,  déterminer le vecteur accélération du centre d'inertie du boulet lors du mouvement. On suppose que les frottements dus à l'air sot négligeables. Le boulet n'est soumis qu'à son poids ; ax = 0 ; ay = -9 = -9,8 m s-2. 2.2. Dans le repère d'espace défini, montrer que les équations horaires du mouvement s'expriment sous la forme : x(t) = v0 cos a t ; y(t)= -½gt2 + v0 sin a t +h. La vitesse est une primitive de l'accélération : vx(t) = A ; vy(t) = -gt +B avec A et B des constantes déterminées par les conditions initiales. vx(t) = v0 cos a ; vy(t) = -gt + v0 sin a . La position est une primitive de la vitesse : x(t) = v0 cos a t + C ; y(t)= -½gt2 + v0 sin a t +D, avec C et D des constantes déterminées par les conditions initiales x(t=0)=0 et y(t=0) = h. x(t) = v0 cos a t ; y(t)= -½gt2 + v0 sin a t +h. 2.3. En déduire l'équation de la trajectoire du centre d'inertie y=f(x). t = x /( v0 cos a ) , repport dans y(t) : y = -½g x2 / (v0 cos a)2 + v0 sin a  x / (v0 cos a) +h. y =  -½g x2 / (v0 cos a)2 +  x  tan a + h. 2.4. Vérifier la valeur du reccord du monde. y = 0 ; -0,5 *9,81 *D2  /(13,7 cos 43)2 + D tan43 +2,75. -0,0489 D2+ 0,933D +2,75 = 0. D2- 19,07D -56,2 = 0. D = 19,072 +4*56,2 =588,6 ; D½ =24,26. On retient la valeur positive : D = (19,07 + 24,26) / 2 = 21,7 m. 2.5. Déterminer la hauteur atteinte par le boulet. Au sommet de la trajectoire, la composante verticale de la vitesse est nulle : vy(t) = -gt + v0 sin a  = 0. t = v0 sin a  / g, repport dans y(t) : yS =-½g (v0 sin a  / g)2 +(v0 sin a  )2 / g + h. yS = ½(v0 sin a  )2 / g +h. yS = 0,5 (13,7*sin43)2 / 9,81 +2,75 = 7,2 m. 3. Comment amméliorer la performance d'un lanceur ? L'entraîneur veut savoir sur quel(s) paramètre(s) travailler pour améliorer la performance de l'athlète. Celui-ci est plus petit que le reccordman du monde, sa taille est telle que l'altitude initiale de ses lancers n'est au maximum que de h' = 2,45 m. L'entraîneur décide donc d'étudier l'influence de la valeur v0 de la vitesse initiale et de l'angle de tir. Il réalise des séries de simulations. 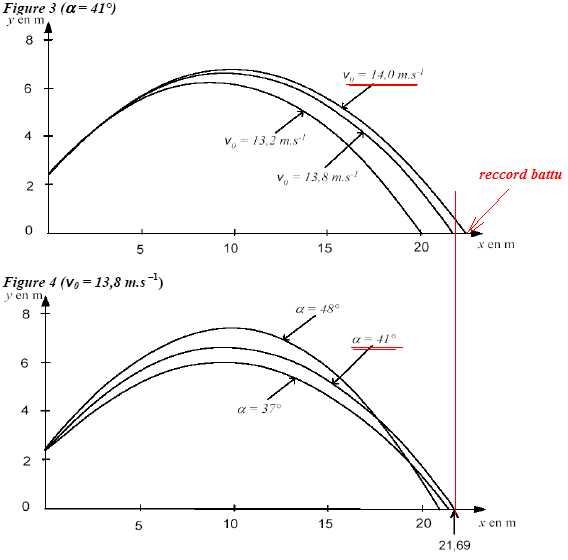3.1. Entourer dans le tableau la réponse correcte. (v0 sin a  )2 / g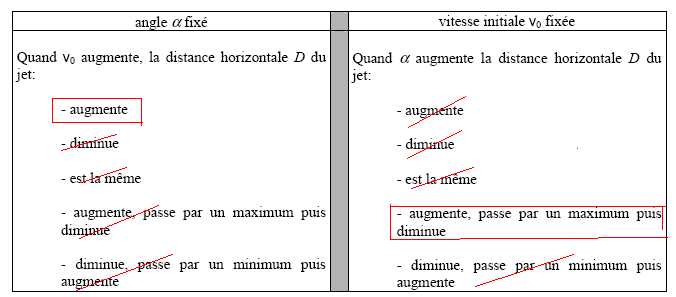 3.2 Déduire parmi les combinaisons proposées, s'il en existe une pour battre le reccord du monde. Justifier. A v0 constante, a = 41° permet d'obtenir la plus longue portée. A a = 41°, constant, v0 = 14,0 m/s permet de battre le reccord u monde.

menu