QCM physique.
Concours kiné Berck 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
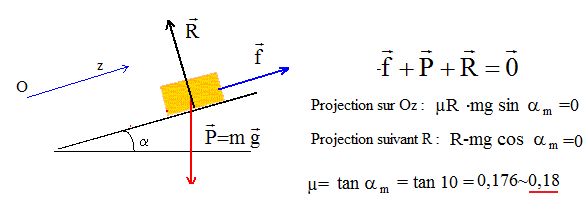
1. Coefficient de
frottement statique.
Lorsqu'il ne glisse pas, le cube est soumis à son poids P, à la
réaction normale du plan R
et à la force de frottement statique f. On cherche à mesurer le
coefficient de frottement statique de l'acier sur acier, noté µ.
On
augmente progressivement l'angle que fait le plan avec l'horizontale et
on constate que le cube reste immobile jusqu'à un angle am=10°C. Pour un
angle supérieur, le cube glisse.
Calculer la valeur de µ
( sans unité).
0,18 ; 0,57 ; 0,70 ; 0,82 ; 0,95 ; aucune réponse exacte.
A la limite du glissement f = µR.
2.
Lancer vertical.
A l'instant t=0, on lance du point A, un
projectile considéré comme ponctuel, avec une vitesse initiale v0
verticale vers le haut. On choisit un axe vertical Oz orienté vers le
haut, l'origine étant au sol. On néglige l'action de l'air sur le
projectile.
On donne zA = 1,8 m et v0 = 18 km/h = 18/3,6 = 5,0 m/s.
Combien y a-t-il d'affirmations exactes ?
- Le sommet de la
trajectoire a pour position zS = 3,1 m. Vrai.
Au sommet, l'énergie mécanique du projectile est sous forme potentielle
mgzS.
En A, l'énergie mécanique du projectile vaut : ½mv02
+ mgzA.
Conservation de l'énergie mécanique : ½mv02
+ mgzA = mgzS.
½v02
/ g+ zA = zS =½v02 / g+ zA =0,5
*52 /9,8 +1,8 ~3,1 m.
- Le projectile atteint le sommet à t = 0,51 s.
Vrai.
Au sommet la vitesse
est nulle : v = -gt +v0 = 0 ; t =v0 / g = 5/9,8
=0,51 s.
- Le projectile
repasse par le point A à t = 1,0 s. Faux.
z = -½gt2 +v0t +zA = -4,9t2+5t+1,8.
1,8= -4,9t2+5t+1,8 ; -4,9t2+5t
=0 soit t=0 et t = 5/4,9 =1,02 s.
- Le projectile
atteint le sol à t = 1,3 s.
Vrai.
0
= -4,9t2+5t+1,8. Disriminant D =25+4*1,8*4,9 = 60,28 ;
Solution positive t =(-5- 7,764) / (-2*4,9) =1,30 s.
- Le projectile
atteint le sol avec une vitesse v = 28 km/h. Vrai.
v
= -gt+v0
= -9,8*1,3 +5 = -7,74 m/s ( le signe moins traduit le fait que la
vitesse est en sens contraire de l'axe ) ; 7,74 *3,6 ~28 km/h.
3. Période de révolution ( an années
) de Pluton autour du soleil.
123 ; 214 ; 248 ; 312 ; 327 ; aucune réponse exacte.
Pluton décrit autour du soleil une orbite élliptique, de demi grand axe
a et de période T.
a = 39,44 ua ; 1 ua = 1,496 1011 m ; Msoleil =
1,989 1030 kg ; 1 année = 365,25 jours.
3éme loi
de Kepler : T2 / a3 = 4p2/(GMsoleil).
a = 39,44 *1,496 1011 =5,90 1012
m.
T2 =4*3,142
*(5,90 1012)3 /(6,67 10-11
*1,989 1030)=6,10 1019 ;
T =7,81 109 s ou 7,81 109 /(3600*24*365,25)~248 ans.
4. Calculer la valeur du
champ de pesanteur ( m s-2) à la surface de Pluton.
0,20
; 0,63 ; 0,85 ; 1,2 ; 1,7 ; aucune réponse exacte.
Rayon de Pluton :
R = 1,19 106 m ; masse volumique de Pluton : r =1,89 103 kg m-3 ;
Masse de Pluton : M=4 /3 p R3 r.
g = GM / R2 = G 4 /3 p R r = 6,67 10-11 *4
/3 *3,14 *1,19 106 *1,89 103 ~0,63 m s-2.
|
|
|
5. Pendule élastique horizontal.
On mesure une durée de 14,5 s pour effectuer 20 oscillations.
On ajoute une surcharge sur le solide m' =75,0 g. On mesure une durée
de 17,0 s pour effectuer 20 oscillations.
Période propre d'un pendule élastique horizontal T = 2 p [M / k]½.
Calculer la valeur de la constante de raideur k ( N m-1) du
ressort.
5,7 ; 15 ; 22 ; 27 ; 32 ; aucune réponse exacte.
Sans surcharge T2 =4p2M /k avec T =
14,5 /20 = 0,725 s.
Avec surcharge T ' 2 =4p2(M+m') /k avec
T ' = 17,0 /20 = 0,85 s.
T
' 2 - T2 =4p2 m' / k ; k = 4p2
m' / [T
' 2 - T2].
k = 4*3,142 *0,075 /(0,852 -0,7252) =15 N m-1.
6. Mesure de la vitesse d'une balle
de pistolet.
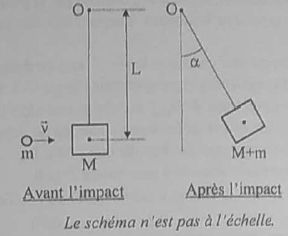
Lors de l'impact la balle s'encastre à l'intérieur du bois. On admet
qu'il y a conservation de la quantité de mouvement du système balle +
bloc lors de l'impact. Le pendule ainsi constitué s'écarte d'un angle
maximal a. On
considère que l'énergie mécanique se conserve lors du mouvement du
pendule.
Longueur du pendule L = 1,20 m ; masse du bloc M = 4,0 kg ; masse
de la balle m = 8,0 g ; a
= 12°.
Calculer la valeur de la vitesse v ( m / s) de la balle avant l'impact.150 ; 190 ; 280 ; 360 ; 420 ; aucune
réponse exacte.
Conservation de la quantité de mouvement : mv = (M+m) V.
Conservation de l'énergie mécanique du pendule : ½(M+m)V2 =
(M+m) gL(1-cosa).
V =[2gL(1-cosa)]½ = [2*9,8*1,20(1-cos12)]½=0,717
m/s.
v = (M+m)V / m =4,008 *0,717 / 0,008 ~360
m/s.
|
|
|
|
7. Célérité du son.
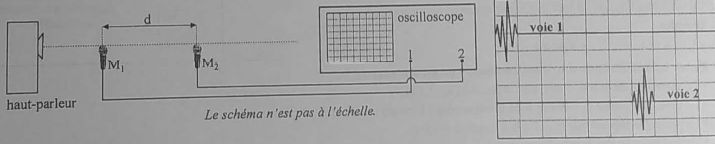
A
l'aide d'un haut-parleur, on produit un son bref devant deux
microphones alignés. Les deux signaux ont été décalés pour faciliter la
lisibilité. L'expérience a été faite à 15°C.
Base de temps de l'oscilloscope 50 µs/div ; célérité du son dans l'air
c = (402 T)½ avec T température absolue.
Calculer d ( en cm).
4,2 ; 8,5 ; 10 ; 24 ; 27 ; aucune réponse exacte.
c = (402*288)½ =340,26 m/s.
Décalage des signaux Dt
= 6*50 = 300 µs = 0,3 ms = 3 10-4 s.
d = c Dt =340,26 *3 10-4
=0,102 m ~ 10 cm.
8. Micro-ondes.
Le magnéton du micro-ondes émet des ondes de fréquence n
= 2,45 GHz. Ces ondes sont absorbées par les molécules d'eau des
aliments ce qui provoque une augentation de température de ces derniers.
Combien y a t-il d'affirmations exactes ?
- L'unité de la constante de Planck est kg m2 s-1. Vrai.
Joule = newton fois distance ; newton =masse fois longueur divisé temps2.
J s =kg m s-2 m s = kg m2 s-1.
- La masse d'un photon est voisine de la masse d'un électron. Faux.
- L'énergie d'un photon émis par le magnéton vaut 1,02 µeV. Faux.
E = h n = 6,63 10-34 *2,45 109 =1,62 10-24 J ou 1,62 10-24 / (1,6 10-19) = 1,02 10-5 eV = 10,2 µeV.
- La longueur d'onde d'un photon émis vaut 12,2 mm. Faux.
l = c / n =3,0 108 /(2,45 109)= 0,122 m =122 mm.
- La valeur de la quantité de mouvement d'un photon émis par le magnéton est p = 5,41 10-32 kg m s-1. Faux.
p = h / l = 6,63 10-34 / 0,122=5,41 10-33 kg m s-1.
9. Niveaux d'énergie de l'atome de sodium.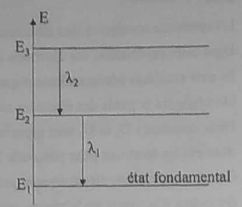
l1 = 589 nm ; l2 = 568,8 nm.
L'atome de sodium, pris dans son état fondamental, est éclairé par un faisceau laser de longueur d'onde l ; il passe du niveau E1 au niveau d'énergie E3. Quelle est la valeur de l ( en nm) ?
289,9 ; 310,3 ; 324,7 ; 578,7 ; 589,0 ; aucune réponse exacte.
E3-E2 = h c / l2 ; E2-E1 = h c / l1 ; E3-E1 = h c / l = h c / l2 +h c / l1 ;
1 / l = 1 / l2 +1 / l1 = 1 / 589 +1 / 568,8 =0,003456 ; l =289 nm.
|
10. Appareil photographique.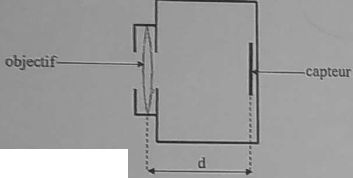
La distance d peut varier entre deux valeurs limites d1<= d <=d2 avec d2-d1 = 3,0 mm.
Cet appareil permet d'obtenir des images nettes d'objets situés à l'infini jusqu'à une distance minimale D de l'objectif.
On donne la vergence de l'objectif C = 20 dioptries.
Calculer D ( en cm).
26 ; 50 ; 55 ; 60 ; 88 ; aucune réponse exacte.
Objet à l'infini : l'image se forme dans le plan focal image de la lentille d1 = 1/20 =0,05 m = 5,0 cm.
Objet à la distance D : l'image nette se forme sur le capteur à d2 =50+3 = 53 mm.
Formule de conjugaison : C = 1/d1 -1/ (-D) ; 1/ D = C - 1/d1 =20-1 /0,053 = 1,132 ; D= 1 /1,132 =0,88 m = 88 cm.
|
|