Physique, concours
ergothérapie Berck 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Question 1.
Lors d'un séisme , la terre est mise en mouvement par des ondes de
différentes natures qui ocasionnent des seccousses plus ou moins
violentes et destructrices en surface. L'épicentre est le point de la
surface de la terre à la verticale du foyer du séisme.
On distingue :
- les ondes P, appelées aussi ondes de compression, se propageant dans les solides et les liquides à la célérité vp ;
- les ondes S, appelées aussi ondes de cisaillement, se propageant uniquement dans les solides à la célérité vS.
l'enregistrement de ces ondes par les sismographes à la surface de la
terre permet de déterminer la position de l'épicentre du séisme. La
formule suivante permet de calculer la distance D entre un sismographe
et l'épicentre du séisme :
D= vP vS Dt / (vP-vS).
Dt désigne l'écart entre les dates d'arrivée des ondes P et S au niveau du sismographe.
On donne vP = 6,0 km /s ; Dt = 5,0 s ; D = 30 km.
Calculer vS en km/s
.(2,0 ; 3,0 ; 4,0 ; 6,0 ; 8,0 ; aucune réponse exacte).
30 = 6 vS*5 / (6-vS) ; 1 = vS / (6-vS) ;
6-vS = vS ; vS =3 km /s.
Question 2.
Pour effectuer un service au tennis, un joueur lance la balle
verticalement vers le haut et la frappe à un instant t=0 avec sa
raquette en un point P. La balle part de P avec une vitesse initiale v0 horizontale.
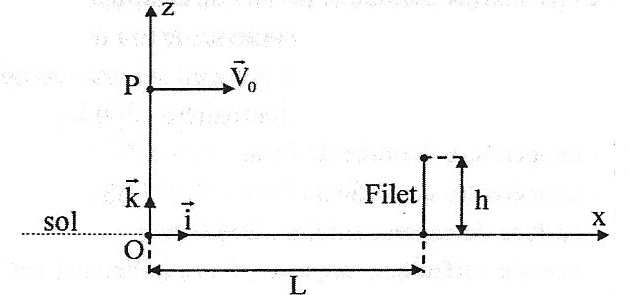
La balle est considérée comme ponctuelle et on étudiera sa trajectoire danns le repère (O, i, j ) indiqué
sur le schéma. L'origine du repère est au niveau du sol et sur la
verticale du point P. Le filet vertical de hauteur h se situe à la
distance L du point O. On suppose que la balle n'est soumise qu'à son
poids.
v0 = 180 km /h ; zP = 2,0 m ; L = 10 m ; h = 90 cm.
Parmi les affirmations suivantes, combien y en a-t-il d'exactes ?
- L'accélération de la balle ne dépend pas de sa masse. Vrai.
- L'équation de la trajectoire de la balle dans le repère s'écrit : z = -x2 / 500 +2,0. Vrai.
Accélération : ax = 0 ; ay = -g = -10.
Vitesse à la date t : vx = v0 = 180 / 3,6 =50 m /s ; vy = -gt = -10 t.
Position : x = v0t = 50 t ; z = -½gt2+zP = -5t2+2,0.
Trajectoire : z = -5x2 / 502 +2,0 = -x2 / 500 +2,0.
- La balle passe 80 cm au dessus du filet. Faux.
z = -L2 / 500 +2,0 = -102 / 500 +2,0 =1,8 m. 1,8-0,90 = 0,90 m = 90 cm.
- La balle touche le sol au point d'abscisse x = 32 m. Vrai.
0 = -x2 / 500 +2,0 ; x2 =1000 ; x ~32 m.
- La balle touche le sol à l'instant t = 0,2 s. Faux.
x = 50 t = 32 ; t = 0,64 s.
|
| .
. |
|
|
Question 3. Relativité restreinte.
Parmi les affirmations suivantes, combien y en a-t-il d'exactes ?
- La théorie de la relativité restreinte a été développée par Newton. Faux ( Einstein)
- Le coefficient g s'exprime en seconde. Faux.
Ce coefficient est sans unité.
- La valeur c de la vitesse de la lumière dans le vide ne dépend pas du référentiel d'étude. Vrai.
- La durée mesurée est toujours inférieure à la durée propre. Faux.
- Si le coefficient g
associé à un électron est égal à 2, alors la valeur de la vitesse de
cet électron dans le référentiel du laboratoire est telle que v = 0,43
c. Faux.
On pose ß2 = v2 / c2 ; g2 = 1 /(1- ß2)
4(1- ß2) = 1 ; 1- ß2 =0,25 ; ß2 =0,75 ; ß ~0,87 ; v = 0,87 c.
Question 4. Loi de Wien.
La valeur de la longueur d'onde la plus intense lmax émise par un corps à sa température T est telle que : lmax T=2,9 103 µm K.
Cette loi permet de déterminer la température de suurface d'une étoile par analyse de son spectre.
L'étude du spectre de l'étoile Rigel a permis de mesurer lmax = 2,7 102 nm.
Calculer la température ( en K ) de surface de cette étoile.
2,7 102 nm = 0,27 µm.
T = 2,9 103 / 0,27 = 1,07 104 K.
|
|
|
|
Question 5.
On éclaire à l'aide d'un laser bleu de longueur d'onde l deux fentes d'Young, notées S1 et S2. La distance enntre les deux fentes sera notée b. Le point O' est le milieu du segment S1S2.
Les franges d'interférences sont observées sur un écran parallèle aux
fenntes et situé à une distance D des fenntes. Le point O est le
projeté orthogonal du point O' sur l'écran.
La position d'un point M de l'écran est repéré par l'abscisse x = OM.
La différence de marche d au point M de l'écran se calcule par : d = S2M-S1M = bx /D.
L'interfrange i est la distance qui sépare deux franges consécutives de même nature.
D = 8,20 m ; l = 445 nm ; i = 4,10 mm.
Calculer b ( en µm).
412 ; 530 ; 620 ; 718 ; 890 ; aucune réponse exacte.
On note x1 la position de la première frange brillante : x1 = i = 4,10 10-3 m.
d =4,10 10-3 b / 8,20 = 5 10-4 b.
La différennce de marche entre la frange centrale et la première frange brillante est égale à l = 445 10-9 m.
b = 445 10-9 / (5 10-4)=4,45 / 5 10-3 =0,89 10-3 m =890 µm.
Question 6.
Un
capteur solaire est un système permettant de convertir l'énergie du
rayonnement solaire en énergie thermique. Cette énergie thermique
permet de chauffer l'eau sanitaire dans un ballon de stockage. Un
capteur a été installé sur le toit d'une maison. Un essai d'utilisation
de cet appareil sur une journée a donné les résultats suivants :
production d'eau chaude journalière : 300 L ;
température d'entrée de l'eau T1 = 15°C ; température de sortie de l'eau : T2 = 55°C ;
surface du capteur : S = 6,0 m2 ; énergie surfaciique moyenne d'ensoleillement sur la journée : 2,1 107 J m-2.
Masse volumique de l'eau r = 1,0 103 kg m-3 ; capacité thermique massique de l'eau c = 4,2 103 J kg-1 °C-1.
Calculer le rendement ( en % ) du capteur.
25 ; 30 ; 35 ; 40 ; 45 ; aucune réponse exacte.
Energie solaire reçue : 2,1 107 x 6,0 = 1,26 108 J.
Energie nécessaire à chauffer l'eau : mC(T2-T1) = 300 *4,2 103 (55-15)=5,04 107 J.
Rendement = 5,04 107 /(1,26 108 )=5,04 / 12,6 = 0,40 ( 40 %).
Question 7.
Une lentille mince convergente de distance focale f ' = 6,0 cm permet de former une image nette, d'un objet réel, sur un écran.
L'objet AB assimilable à un segment, est perpendiculaire à l'axe
optique de la lentille et le point A est situé sur l'axe optique.
L'objet AB se situe 8,0 cm devant le cenntre optique O de la lentille.
L'image A'B' est réelle, renversée et trois fois plus grande que l'objet.
L'écran se situe à la distance D de l'objet AB.
Calculer D ( en cm).
24 ; 32 ; 38 ; 44 ; 48 ; aucune réponse exacte.
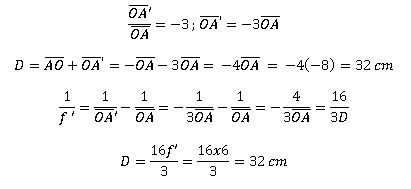
|
Question
8.
Le diagramme ci-dessous repprésente certains niveaux d'énergie ( sans souci d'échelle) d'un atome. E1 désigne l'état fondamental, c'est à dire son niveau de pluis basse énergie. E2 et E3 sont des états excités. Lorsque l'atome passe de l'état excité E3 à l'état fondamental, il émet un rayonnement de longueur d'onde l31. Lorsque l'atome passe de l'état E2 à l'état E1, il émet un rayonnement de longueur d'onde l21. Lorsque l'atome passe de l'état E3 à l'état E2, il émet un rayonnement de longueur d'onde l32.
On propose différentes expressions pour la longueur d'onde l32 en fonction de l31 et l21.
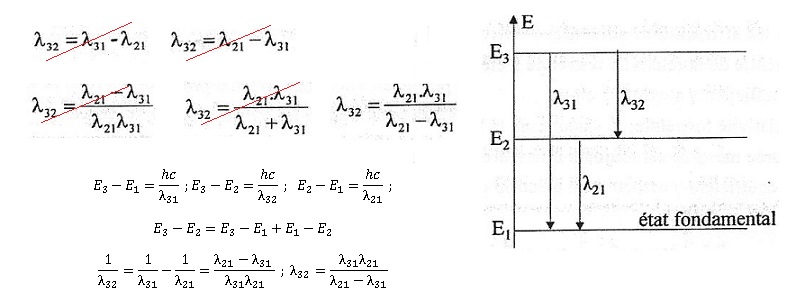
|
|