QCM
physique.
Concours kiné EFOM 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1.
Un
oeil humain emmétrope, c'est à dire normal, peut être modélisé par une
lentille mince convergente L, jouant le rôle de cristallin, située à
une distance fixe d d'un écran E, jouant le rôle de la rétine. Le
cristallin diffère d'une simple lentille par la faculté qu'il a de
pouvoir être déformé par les muscles ciliaires, ce qui modifie sa
distance focale et donc la vergence c = 1 / f '. Le but de cette
déformation étant que l'image d'un objet observé se forme toujours sur
la rétine pour être vue nettement. On donne d = 15 mm. 1/3 ~0,333 ; 1/5
= 0,2.
a. La vergence C d'un oeil emmétrope est de 67 dioptries lorsqu'il observe un objet situé à l'infini.
1/ OA = 0 ; C =1/OA' = 1/ 0,015 =1000 / 15 = 200 / 3 ~2*33,3 ~67 d. Vrai.
b. La distance focale du cristallin diminue lorsque la distance qui sépare l'oeil de l'objet observé diminue. Vrai.
OA' = constante ; -1/OA est positif et croît ; la vergence augmente et la distance focale diminue.
c. Un objet de 10
cm de haut, placé à 75 cm du cristallin de cet oeil conduit à la
formation d'une image de 2,0 mm de haut sur la rétine. Vrai.
Valeur absolue du grandissement : OA' / OA = 1,5 / 75 = 0,02
Hauteur de l'image : 10*0,02 = 0,2 cm = 2 mm.
d. Dans le cas de l'observation d'un objet placé devant cet oeil et pour lequel le grandissement est tel que 0 > g >-1, alors l'image est réelle et plus petite que l'objet. Vrai.
Exercice 2.
On considère une lentille mince convergente de distance focale f ' = 3,0 cm.
a. Les foyers
principaux objet F et image F' de cette lentille sont tels que
mesure algébrique de OF' = mesure algébrique de OF. Faux.
b. Un rayon
lumineux incident qui frappe cette lentille parallèlement à son axe
optique principal, en un point proche de son centre optique, en émerge
dans une direction qui passe par son foyer principal objet. Faux.
....qui passe par son foyer principal image.
c.
Un objet placé entre le foyer principal objet F et le centre optique O
de la lentille conduit à la formation d'une image qui ne peut pas être
recueillie sur un écran. Vrai.
La lentille fonctionne en loupe.
d. La vergence de cette lentille est de 0,33 dioptrie ( 0,33 m-1). Faux.
C = 1 /0,03 = 100 / 3 ~33,3 dioptries.
Exercice 3.
On assimile un mur en granite à une paroi plane de longueur L = 4,0 m,
de hauteur h = 2,5 m et d'épaisseur e. Un après midi d'hiver un système
de chauffage permet de maintenir une différence de température de 20°C
entre l'intérieur et l'extérieur de la maison. Le flux thermique
traversant ce mur est de 500 W. lgranite = 2,2 SI ; l calcaire = 1,0 SI.
a. La résistance thermique du mur en granite vaut 40 mW °C-1. Faux.
Rth = DT / F = 20 / 500 = 0,04 °C W-1.
b. La conductivité thermique l s'exprime en W m-1 K-1. Vrai.
c. L'épaisseur du mur est d'environ 88 cm. Vrai.
Rth = e / (l S) ; e = Rthl S = 0,04*2,2 *4*2,5 = 0,88 m = 88 cm.
d. Toute chose égale par ailleurs, le calcaire est plus adapté que le granite pour réduire le flux thermique. Vrai.
Rth calcaire = 0,88 / (1*2,5*4) =0,088 °C W-1. Flux = 20 / 0,088 ~230 W.
Exercice 4.
Un film d'eau savonneuse d'indice de réfraction n=1,5 et
d'épaisseur e est éclairé par une lumière polychromatique. La lumière
subit deux réflexions: une sur la face supérieure du film et l'autre
sur la face inférieure.. Ces deux ondes réfléchies peuvent alors
interférer.
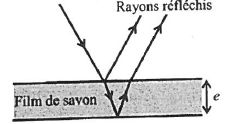
L'angle d'incidence étant très faible, la différence de marche entre les ondes réfléchies, de longueur d'onde l, s'eprime par d = 2 n e +½l.
a. Pour une épaisseur donnée du film, les interférences ne sont constructives que pour une unique radiation. Faux.
2 n e +½l = k l avec k entier. l =2ne / (k-0,5).
b. Pour ce film, les interférences sont toujours destructives si e = l. Vrai.
d=2 n l +½l =(2n+0,5) l = (4n+1)l/2.
c. L'épaisseur du film permettant des interférences constructives pour la radiation l = 600 nm dans le vide doit être au moins égale à 0,10 µm. Faux.
2 n e +½l = k l avec k entier ; e = (k-0,5) l / (2n) =(k-0,5)*0,6 / 3 = 0,2 (k-0,5).
Pour k = 1 : e =0,1 µm.
Il faudrait écrire " égale à ", pour e = 0,11 µm, les interférences ne sont pas constructives pour cette longueur d'onde.
d. Si l'épaisseur du film est inférieure à 10 nm, aucune radiation visible ne peut interférer de façon constructive. Vrai.
l =2ne / (k-0,5) = 3*10/(k-0,5) =30 /(k-0,5) nm. k=1 , lmax = 60 nm.
Exercice 5.
Un
laser émet dans le vide une lumière de longueur d'onde l = 640 nm. Ce
faisceau éclaire une fente horizontale de largeur a. On observe une
figure lumineuse produite sur un écran situé à la distance D = 2,0 m de
la fente, l'écran étant perpendiculaire à la direction du faisceau
laser. On donne 4,7 *6,4 ~30.
a. La fréquence de l'onde électromagnétique émise par le laser vaut 4,7 1014 Hz. Vrai.
f = c / l = 3 108 / (640 10-9) = 30 /6,4 1014 = 4,7 1014 Hz.
b. On observe une figure d'interférences lumineuses sur l'écran. Faux ( diffraction).
c. La figure lumineuse est horizontale. Faux ( verticale ).
d. La figure lumineuse voit son allure modifiée si on augmente la distance séparant le laser de la fente. Faux.
|
|
|
Exercice 6.
L'expérience des fentes d'Young est réalisée avec une lumière monochromatique de longueur d'onde l
éclairant deux fines fentes distantes de b = 4,0 mm. Un écran blanc est
placé à la distance D = 2,0 m des fentes, perpendiculairement au
faisceau d'ondes. On observe une figure d'interférences sur l'écran. ;
interfrange i = lD / b = 6,0 mm.
a. La figure d'interférences peut être observée à l'oeil nu. Vrai.
b. En un point de l'écran où se produit une interférence constructive, la différence de marche d est nécessairement nulle. Faux.
c. Pour l'expérience décrite, lorsqu'on utilise un laser vert à la place d'un laser rouge, l'interfrange diminue. Vrai.
L'interfrange est proportionnel à l et lvert < lrouge.
d. On obtient une
figure d'interférences similaire en utilisant deux lasers distincts
émettant un rayonnement de même longueur d'onde et éclairant chacun une
des deux fentes. Faux.
Les ondes ne sont pas synchrones.
Exercice 7.
On considère l'équation de la réaction nucléaire suivante :
23592U +10n --->15462Sm +7930Zn +x10n.
a. Le défaut de masse d'un noyau est une grandeur de valeur négative. Faux.
Masse des protons + masse des neutrons - masse du noyau. La masse du
noyau est inférieure à la masse de ces constituants isolés au repos.
b. Il s'agit d'une réaction de fusion nucléiare. Faux, ( fission d'un gros noyau instable).
c. La valeur de x est égale à 3. Vrai.
Conservation du nombre de nucléons : 236 = 154+79+x ; x = 3.
d. La fusion nucléaire est une transformation spontanée. Faux.
Exercice 8.
Le carbone 14 146C est un noyau radioactif. Sa désintégration s'accompagne de l'émission d'un électron. On enregistre 1,2 104 désintégrations pendant 10 minutes pour un échantillon de carbone 14.
a. Le noyau ce carbone 14 contient 14 neutrons. Faux ( 8 neutrons et 6 protons).
b. Le noyau obtenu par désintégration d'un noyau de carbone 14 contient 7 protons. Vrai.
146C ---> 147N +0-1e.
c. L'activité de l'échantillon étudiée vaut 1,2 kBq. Faux.
1,2 104 / (60*10) = 20 Bq.
d. La masse de l'échantillon reste inchangée au cours des désintégrations. Faux.
D. Une incertitude relative sur une grandeur X peut être négative. Faux.
|
|
|
|
Exercice 9.
On
donne un mouvement vertical périodique à l'extrémité d'une corde
initialement horizontale et au repos. L'onde progressive sinusoïdale
créée se propage le long de la corde à la célérité v = 3,0 m/s. Les
graphiques ci-après représentent l'évolution temporelle de l'élongation
s de deux points de la corde situés aux abscisses x =0 et x = 6 m.

a. L'onde formée est mécanique. Vrai.
b. La période temporelle de l'onde vaut 4 s. Faux, T = 8 s ).
c. La période spatiale de l'onde est 12 m. Faux.
l = vT = 3,0 *8 = 24 m.
d. L'onde se propage dans le sens des abscisses décroissantes. Faux.
Exercice 10.
Le
klaxon d'une voiture à l'arrêt émet un son sinusoïdal de fréquence f =
480 Hz. Alors que la voiture se déplace à vitesse constante en
klaxonnant, un piéton immobile sur le trotoir perçoit un son de
fréquence f '=504 Hz.
Célérité du son dans l'air cson = 340 m/s..
La modification de la fréquence par effet Doppler est donnée par : |Df| = f v / cson.
a. Le son perçu par le pièton lorsque la voiture roule est plus grave que lorsqu'elle est à l'arrêt. Faux.
f ' > f ; plus la fréquence est grande, plus le son est aigu.
b. La voiture s'éloigne du piéton. Faux.
c. La vitesse de la voiture est égale à 17 km/h. Faux.
Df = 504-480 = 24 Hz ; v = Df cson / f = 24 *430 / 480 = 430 / 20 = 43 /2 =21,5 m/s ou 21,5*3,6 = 77,4 km/h.
d. La longueur
d'onde du son perçu par le piéton lorsque la voiture roule est plus
petite que celle du son perçu lorsqu'elle est immobile. Vrai.
Plus la fréquence est élevée, plus la longueur d'onde est faible.
Exercice 11.
A l'aide d'un logiciel de traitement du son, il est possible de créer
des tensions U périodiques d'allures très variées, lesquelles pourront
conduire à des signaux sonores après avoir été amplifiées puis
appliquées aux bornes d'un haut parleur. On donne ci-après l'évolution
temporelle d'une tension U produite avec ce logiciel.
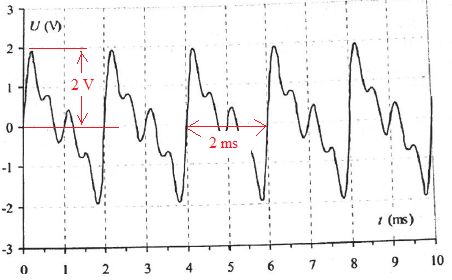
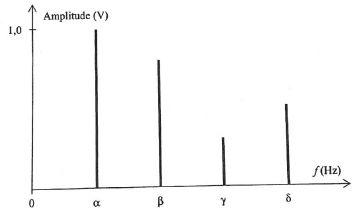
La décomposition de Fourier de ce signal conduit au spectre en fréquences ci-après :
a. l'amplitude du signal est 1,0 V. Faux ( A = 2 V).
b. La période est de 1,0 ms. Faux ( T = 2 ms).
c. L'amplitude de l'harmonique notée d est de 0,50 V. Vrai.
d. La fréquence notée g vaut 1500 Hz. Vrai.
Fréquence du fondamental f0 = 1/T = 1 /0,002 = 500 Hz.
La fréquence de la troisième harmonique vaut 3*500 = 1500 Hz.
|
|