QCM
physique.
Concours kiné Ceerrf 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1.
On
considère un mobile ponctuel de masse m = 250 g sur un banc à coussin
d'air, incliné d'un angle h = 60,0° par rapport à la verticale. Le
mobile est lâché sans vitesse de l'extrémité supérieure du banc noté S.
Le point le plus bas est noté O. On donne g = 10,0 m s-2 et (3,125)½ = 1,75.
1. Exprimer la vitesse du mobile quand il a parcouru la distance D = SO = 2,50 m.
L'énergie
mécanique initiale est sous forme potentielle : mgD sin ( 90-h) = mgD
cos h. L'origine de l'énergie potentielle est prise en O.
L'énergie mécanique en O est sous forme cinétique : ½mv2.
Conservation de l'énergie mécanique du solide de masse m : ( cos h =cos 60 = 0,5).
mgD cos h =½mv2 ; v2 = 2gD cos h = gD ; v = (gD)½. Réponse A.
2. Exprimer la vitesse du mobile quand il lui reste les 2/3 de la distance D à parcourir.
L'énergie
mécanique initiale est sous forme potentielle : mgD sin ( 90-h) = mgD
cos h.
Energie mécanique finale : ½mv2 +mg 2D / 3 cos h.
Conservation de l'énergie mécanique :
mgD
cos h = ½mv2 +mg 2D / 3 cos h.
v2 = 2gD / 3 cos h = gD /3; v = (2gD /3 cos h)½. Réponse E.
3. La
coordonnée y du centre d'inertie G du mobile est définie sur l'axe Oy,
parallèle au banc et orienté vers le haut ( origine en O) ; dans un
second lancer, on communique au mobile placé au milieu I du banc, une
vitesse initiale de valeur vI, et dirigée vers S. Calculer vI pour que le point le plus haut atteint par G soit S.
Energie
mécanique initiale : mgD /2
cos h +½mvI2.
Energie mécanique finale : mg D cos h.
Conservation de l'énergie mécanique : mgD /2
cos h =½mvI2.vI2 = gD cos h = 10*2,50 cos 60 =12,5 = 4*3,125. vI ~2*1,75 = 3,50. Réponse C.
4. Au
cours du précédent mouvement entre I et S, la variation d'énergie
potentielle de pesanteur en fonction de la coordonnée y, peut s'écrire :
Energie potentielle initiale : mgD /2
cos h.
Energie potentielle à la date t : mg y
cos h.
Variation de l'énergie potentielle :
mg (y-½D)cos h =0,25*10(y-1,25) cos 60 =1,25 (y-1,25). Réponse B.
5. Au cours du précédent mouvement entre I et S, l'énergie mécanique du mobile vérifie :
l'énergie méanique étant constante, on l'exprime en S.
EM = mgD cos h = 0,25 *10 *2,5 cos 60 =3,125 =25 / 8 J. Réponse A.
Exercice 2.
On
considère une association de lentilles, assimilable à une lentille
mince (L) convergente, de vergence C et de centre optique O. Cette
lentille donne d'un objet AB une image A'B'. A est situé sur l'axe
optique. O note g le grandissement transversal. La distance objet lentille est notée D = AA'.
6. Objet et image vérifient :
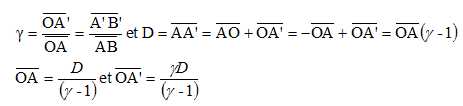
Réponses B et E.
7.
Pour calculer le grandissement, on peut passer par la résolution d'une
équattion différenteille du second degré dont l'expression peut être :
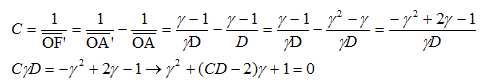
Réponse E.8. La résolution de cette équation aboutit à un grandissement égal à :
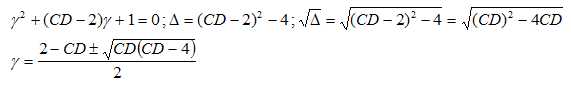
Réponse F.9. Si C = 2,5 d et D = 1,60 m, le grandissement a pour valeur :
CD = 4 ; g =1-2 = -1. Réponse C.
10. On utilise maintenant une autre lentille L1 de vergence C1 = 2 C. Elle donne d'un objet AB situé 40 cm à gauche du foyer objet F'1, une image A'B' :
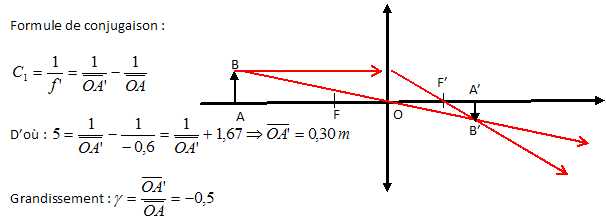
Image réelle et inversée située à 10 cm à droite de F'. Réponses A et D.
|
|
|
Exercice 3.
On considère un condensateur plan. Entre les armatures verticales A et B de ce condensateur, on applique une tension UAB positive. Les armatures ont pour longueur L, elles sont planes et parallèles et la distance entre elles est notée d.
Entre ces armatures, on place une charge électrique q. Cette charge est
une petite goutte d'huile électrisée de masse m qui possède un excès de
106 électrons.
UAB = 1,0 105 V ; d = 1,0 cm ; L = 30 cm ; m = 2,0 10-4 g ; e = 1,6 10-19 C; g = 10 SI.
11. En fonction des unités de base, le champ électrique noté E, s'exprime en :
E = UAB / d s'exprime en V m-1.
Tension = énergie / ( intensité fois temps) soit J A-1 s-1.
Energie = force fois distance et force = masse fois distance / temps2.
Une énergie s'exprime en kg m2 s-2.
E s'exprime en : kg m s-3 A-1. Réponse D.
12. A propos des incertitudes.
A. Une incertitude absolue sur une grandeur X s'exprime en pourcentage. Faux.
B. Une incertitude absolue sur une grandeur X s'exprime dans la même unité que celle de X. Vrai.
C. Une incertitude relative sur une grandeur X peut s'exprimer en pourcentage. Vrai.
D. Une incertitude relative sur une grandeur X peut être négative. Faux.
E. Une incertitude relative sur une grandeur X s'exprime dans la même unité que celle de X. Faux.
F. Aucune proposition ne convient.
13. A propos de la goutte d'huile placée dans le condensateur plan.
A. Le sens du champ électrique créé entre les armatures dépend du signe de la charge q. Faux.
Le sens du champ dépend du signe de la tension UAB.
B. Le champ électtrique dans la région centrale du condensateur peut
être considéré comme uniforme et sa valeur est égale à : -1,0 107 V m-1. Faux.
|UAB| / d = 1,0 105 / 0,01 = 1,0 107 V m-1.
C. Le champ électrique dans la région centrale du condensateur est vertical. Faux.
Le champ électrique est perpendiculaire aux plaques verticales, donc horizontal.
D. La goutte d'huile est attirée par l'armature A positive. Vrai.
E. La goutte d'huile subit une force électrique de valeur 1,6 10-6 N. Vrai.
F = |q| E = 1,6 10-19 *106 *107 = 1,6 10-6 N.
14. Abandonnée à elle même, la goutte d'huile subit une accélération qui a pour valeur :
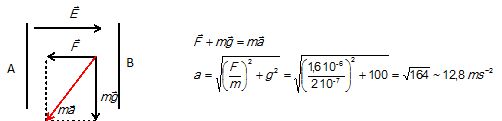
Réponse F.
15. les plaques
sont maintenant placées horizontalement et on veut maintenir la goutte
précédente en équilibre. Elle est initialement dans la région centrale
des plaques.
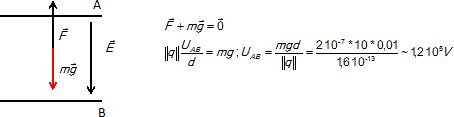
La plaque A est au dessus de la plaque B et il faut augmenter la tension UAB.
Réponse A.
|
|
|
|
Exercice 4.
16. A propos de l'homogénéité d'une formule.
A. Lorsque qu'une relation est homogène en dimension, elle est forcément exacte. Faux.
B. Toute grandeur physique possède une dimension. Vrai.
C. Dans une formule mathématique, telle que exp(u), ln (u) ou cos (u), u doit être sans dimension. Vrai.
D. Dans une relation du type x y + z2 = t2, on peut dire que z et t ont la même dimension. Vrai.
E. Dans une relation du type x y + z2 = t2, on peut dire que y a la même dimension que t. Faux.
17. La célérité du son dans un gaz est donnée par la relation v = K pa rß où p est la presion du gaz et r sa masse volumique. K est une constante sans dimension. Les valeurs de a et ß sont :
La masse volumique s'exprime en kg m-3 ; la célérité s'exprime en m s-1.
Une pression est une force divisée par une surface et une force est une masse fois une accélération.
La pression s'exprime en N m-2 ou en kg m-1 s-2.
m s-1 = kga m-a s-2a kgß m-3ß ;
On identifie : a+ß=0 et -2a = -1 soit a = +½ et ß = -½. Réponse E.
18. On suppose que vous vous
dirigez à vitesse constante v = 34,0 m/s vers une source sonore
périodique. Vous entendez cette source avec une fréquence f ' = 1,10
kHz ; cson = c = 340 m/s.
A. Les ondes sonores sont des ondes transversales. Faux.
B. Les ondes sonores sont des ondes à trois dimensions. Vrai.
C. La fréquence réelle de la source sonore lorsque vous vous arrétez près d'elle est de 1,10 kHz. Faux.
D. La fréquence réelle de la source sonore lorsque vous vous arrétez près d'elle est de 1,00 kHz. Vrai.
f ' = f c / (c-v) = f *340 / (340-34) ~1,11 f ; f = f ' / 1,11 = 1,10 / 1,11 ~ 1,0 kHz.
E. La fréquence réelle de la source sonore lorsque vous vous arrétez près d'elle est de 1,21 kHz. Faux.
19.On réalise l'expérience des
fentes d'Young avec deux fentes distantes de a = 2,00 mm. Le système
d'interférences se forme sur un écran translucide à une distance D =
2,00 m des fentes. On place ensuite une lentille de vergence C = 10,0
dioptries à 12 cm de l'écran translucide. On observe alors l'image de
la figure d'interférences sur un autre écran E' situé à D' = 60,0 cm de
la lentille. L'interfrange mesuré sur l'écran E' vaut i '= 2,50 mm. La
longueur d'onde de la lumière utilisée a pour valeur :
Valeur absolue du grandissement : |g|=60,0 / 12 = 5,0.
Valeur de l'interfrance sur l'écran E : i = i' / 5 = 2,50 / 5 = 0,50 mm = 5,0 10-4 m.
i = lD / a ; l = i a / D = 5,0 10-4 *2,0 10-3 / 2,0 = 5,0 10-7 m = 500 nm. Réponse B.
20. Un coup sec est porté sur
une canalisation en métal dans laquelle circule un gaz. Un capteur
situé à la distance d = 300 m du point d'application du coup
enregistre deux signaux xonores brefs séparés par une durée Dt = 300 ms.
On donne la célérité du son dans le gaz c = 0,80 km/s. La célérité du son dans le métal de la canalisation est :
d = ct1 ; d = cmétal t2 ; t1-t2 = Dt =d / c -d / cmétal ;
d / cmétal = d / c - Dt =300 / 800 -0,3 =0,075 s
cmétal =300 / 0,075 = 4000 m/s = 4,0 km/s. Réponse E.
|
|