QCM Ondes. Concours audioprothèsiste Bordeaux 2016.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.


Une seule réponse juste par question. Des points négatifs seront affectés en cas de réponses fausses..
1. Un camion s'approche à vitesse constante V de Robert, immobile sur le côté de la route.
Plus le camion s'approche, plus le son est aigu. Faux.
Plus le camion s'approche, plus le son est grave. Faux.
La fréquence perçue par Robert est la même tout au long de l'approche du camion. Vrai.
La fréquence perçue par Robert est nulle puisque celui-ci est immobile. Faux.
La fréquence reçue par Robert est identique à la fréquence émise par le camion tant que ce dernier a une vitesse constante. Faux.

   2. On rappelle la formule générale conncernant l'effet Doppler ( valable tant que Vémetteur et Vrécepteur << c).
Fperçue = F[(c-Vrécepteur ) / (c-Vémetteur)]
c : vitesse de propagation du son.;
Vémetteur : projection algébrique de la vitesse de l'émetteur ( sens + = sens de propagation du son).
Vrécepteur : projection algébrique de la vitesse du récepteur.

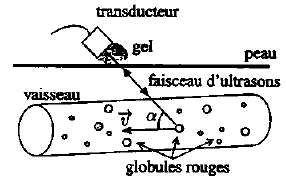La vitesse du flux sanguin peut être déterminée à partir de la formule :
V = 2c / f dF ; V = cdF / (F cos a) ; V = cdF / (2F cos a)  vrai ; V = cdF / (F cos a). 
 
3. Un piéton proche d'une voie ferrée observe un TGV sedéolaçant à 250 km/h. Celui-ci émet un signal sonore de fréquence 1,5 kHz. On négligera la distance piéton-voie ferrée. La féquence perçue par l'observateur juste avant le passage du TGV est ( en Hz) :
1890, vrai ; 1630 ; 1250 ; 2240 ; 390.
Fperçue = F[ c / (c-Vémetteur)] avec Vémetteur = 250 / 3,6 ~69,5 m /s.
Fperçue = 1500 [340 / (340-69,5)] ~1890 Hz.

 4. Un piéton proche d'une voie ferrée observe un TGV sedéolaçant à 250 km/h. Celui-ci émet un signal sonore de fréquence 1,5 kHz. On négligera la distance piéton-voie ferrée. La féquence perçue par l'observateur juste après le passage du TGV est ( en Hz) :
1890 ; 1630 ; 1250, vrai ; 2240 ; 390.
Fperçue = F[ c / (c+Vémetteur)] .
Fperçue = 1500 [340 / (340+69,5)] ~1250 Hz.

 5. Une ambulance est animée d'un mouvement rectiligne uniforme de vitesse V. Un observateur entend un son de fréquence 1150 Hz lorsqu'elle s'approche de lui et de 960 Hz lorsqu'elle s'en éloigne. La vitesse de l'ambulance est  ( en km /h) :
108 ; 90 ; 145 ; 117 ; 110, vrai.
Approche : Fperçue = F[ c / (c-Vémetteur)] ; 1150 = F(c / (c-V).
Eloignement : Fperçue = F[ c / (c+Vémetteur)] ; 550 = F(c /(c+V).
1150 / 960 ~1,198 = (c+V) / c-V)  ; V = 0,198 c / 2,198 = 0,09 c = 30,6 m/s
ou 30,6 *3,6 = 110 km/h.
 
6. On rappelle que l'intensité sonore en champ libre décroît en 1 / r2 ( où r désigne la distance par rapport à la source ). Dans un aéroport, la distance limite où le seuil de la douleur ( 120 dB) est atteint à 6 m d'un avion au décollage. Par rapport à cette position, de combien de mètres doit-on reculer pour percevoir une intensité sonore de 60 dB ?
5000 m ; 6006 m ; 6000 m ; 3000 m ; 5994 m, vrai.
A 6 m : I = I0 100,1 L = I0 1012 ; A x m : I '= I0 106 ; I / I' =106.
I = Cste / 62 ; I' = Cste / d2 ; I / I' =d2 / 36 ; d2 = 36 106 ; d = 6 000 m.
On doit reculer de 6000-6 = 5994 m.

 7. On appelle niveau équivalent d'une campagne de mesure de niveaux sonores le niveau moyen durant la durée de la campagne. Léq = 10 log(Imoyen / I0).
Concernant la campagne de mesure suivante, Léq est égal à ( en dB) :
63,2 ; 67,5 ; 66,3 ; 64,0 ; 65,4.

Imoyen = I0( 107 +106,8 +106,3+106,5+106+106) / 6 =3,91 106 I0.
Léq = 10 log (3,91 106) = 65,9 dB.

8. Lorsqu'on étudie le niveau sonore et que l'on désire avoir une information quant à la répartition en fréquence de l'énergie, on mesure le niveau sonore par bande d'octave. Le niveau sonore global correspond alors à la somme des intensités dans les différentes bandes d'octaves. Concernant la répartition par bande d'octave suivante, Lglobal est égal à ( en dB) :
73,2 ; 61,9 ; 72,6 ; 64,8 ; 433.
Bande d'octave (Hz)62125250500100020004000
Niveau sonore L( dB)70686357605758
I =I0 100,1 L10-56,31 10-62,0 10-65,01 10-710-65,01 10-76,31 10-7
Itotal =10-5+6,31 10-6 +2,0 10-6 + 5,01 10-7+10-6 +5,01 10-7 +6,31 10-7 =2,09 10-5 Wm-2.
L = 10 log [ Itotal / I0] =10 log [(2,09 10-5 / 10-12) =73,2 dB.

.
.




9. Lorsque l'on désire tenir compte de la réponse de l'oreille qui n'est pas identiquequement sensible à toutes les fréquences, on applique une correction aux niveaux sonores L par bandes d'octave en pondérant chaque niveau par un coefficient normalisé. L'unité devient alors dB(A) au lieu de dB.
Bande d'octave (Hz)62125250500100020004000
Pondération (dB)-26-16,1-8,6-3,20+2+1
L (dB(A)) = L (dB) + Pondération.
Un son à 500 Hz est perçu comme plus fort qu'un son à 1 kHz de même niveau sonore. Faux.
Des sons de mêmes niveau sonore en dB à 1 kHz et 500 Hz sont perçus comme étant aussi forts l'un que l'autre. Faux.
C'est à 1000 Hz que nous entendons le mieux. Vrai.
Nous somme sourds vers 3 KHz et entendons très bien dans les graves. Faux.
Nous sommes sourds dans les graves et entendons très bien vers 3 kHz. Faux.

 10. En tenant compte des pondérations précédenntes, calculer le niveau global en dB(A) du son de la question 8. 73,2 ; 65,0 ; 72,3 ; 64,2.
Bande d'octave (Hz)62125250500100020004000
Niveau sonore L( dB(A)70-26
=44		68-16,1
=51,9		63-8,6
=54,4		57-3,2
=53,8		6057+2
=59		58+1
=59
I =I0 100,1 L2,5110-81,55 10-72,75 10-72,4 10-710-67,94 10-77,94 10-7
Itotal =2,5110-8+1,55 10-7 +2,75 10-7 + 2,4 10-7+10-6 +7,94 10-7 +7,94 10-7 =3,28 10-6 Wm-2.
L = 10 log [ Itotal / I0] =10 log [(3,28 10-6 / 10-12) ~65 dB.

  11..Une chorale dispose de 4 chanteurs. Si on souhaite augmenter le niveau sonore de 15 dB, combien de chanteurs devons-nous ajouter ? 112 ; 12 ; 123 ; 127 ; 60.
Linitial = 10 log (Iinitial / I0) ; Lfinal = 10 log (Ifinal / I0).
Lfinal -Linitial =15 = 10 log (Ifinal / Iinitial) ; Ifinal / Iinitial = 101,5 = 31,6.
Intensité sonore correspondant à un chanteur :0,25 I initial ;
Intensité sonore correspondant à n chanteurs : Ifinal  = 0,25 n Iinitial =31,6 Iinitial  ;
n = 31,6 /0,25 ~127.









12. A 4 m d'un haut-parleur, l'intensité sonore vaut 6,2 10-5 W m-2. A quelle distance ( en m)  du haut-parleur faut-il se positionner si on souhaite un niveau sonore de 58 dB ? 53 ; 12 ; 32 ; 40 ; 24.
A 4 m : I =Cste / 42 = 6,2 10-5 W m-2.
A x mètre : I' = Cste / x2 = 10-6,2 = 6,3 10-7 W m-2.
I / I' = x2 / 16 = 98 ; x2 = 16*98 =1572 ; x ~40 m. 

13. Un chanteur seul produit un niveau sonore de 75 dB à 5 m. Combien de chanteurs de même niveau sonore faut-il pour produire le même niveau à 20 m ? 40 ; 16 ; 10 ; 2 ; 20.
A 5 m et un chanteur : I =Cste / 52 = 3,16 10-5 W m-2.
A 20 m et un chanteur : I' =Cste / 202  ;
I' / I = 52 / 202 = 0,0625. ; I' = 1,975 10-6 W m-2.
A 20 mètres et x chanteurs : x I' =  3,16 10-5 W m-2.
x = 3,16 10-5  / (1,975 10-6) =16.
14. Dans un jardin en bord de rocarde, le niveau sonore global est de 75,0 dB en présence du bruit de la circulation et de la tondeuse du voisin. Lorsque la tondeuse s'arrête,le niveau sonore tombe à 68 dB. Pouvez-vous en déduire le niveau sonore de la tondeuse seule ?
60,1 dB ; 7,0 dB ; 74,0 dB ; 61,0 dB ; 66,5 dB.
I circulation = 10-12 *106,8 = 10-5,2 =6,3 10-6 Wm-2.
I total = 10-12 *107,5 = 10-4,5 =3,16 10-5 Wm-2.
Itondeuse = I total -I circulation =3,16 10-5 -6,3 10-6  =2,53 10-5 Wm-2.
Ltondeuse = 10 log( 2,53 10-5/ 10-12)=74 dB.

15. Trois bruits de 0 dB parviennent à l'oreille d'une personne .Le niveau sonore total sera ( en dB) : 3,0 ; 0,0 ; 4,5 ; 6,0 ; 4,8.
Itotal = 3 10-12 Wm-2. L = 10 log( 3 10-12 / 10-12) =4,8 dB.

16. Pour un système solide-ressort ( m : masse du solide, k constante de raideur du ressort, masse du ressort négligeable ) oscillant sans frottement le long de l'axe Ox, son équation de mouvement en fonction du temps est donnée par :
d2x/dt2 -m / k x=0 ; d2x/dt2 +m / k x=0 ; d2x/dt2 +k / m x=0, vrai.

17. Une fente de largeur a est éclairée  par un faisceau laser. Pour différentes largeurs de fente,  on a mesuré la demi-largeur angulaire q de la tache centrale de la figure obtenue sur un écran. Les  résultats ont permis d'obtenir le graphe ci-dessous sur lequel une interpolation linéaire a été effectuée. Déduisez-en la longueur d'onde du laser ( en nm). 412 ; 236 ;186 ; 576 ; 512.

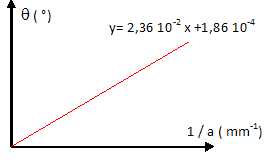
q = l /a. La pente de la droite est égale à la longueur d'onde.
q doit être en radian et a en mètre.
l = 2,36 10-2 *3,14 / 180 x 10-3 = 4,12 10-7 m = 412 nm.
18. Une fente de largeur a est éclairée  par un faisceau laser. Pour différentes largeurs de fente, on a mesuré la demi-largeur ½L de la tache centrale de la figure obtenue sur un écran situé à D = 70 cm de la fente. Les  résultats ont permis d'obtenir le graphe ci-dessous sur lequel une interpolation linéaire a été effectuée. Déduisez-en la longueur d'onde du laser ( en nm). 702 ; 620 ; 434 ; 512 ; 408.

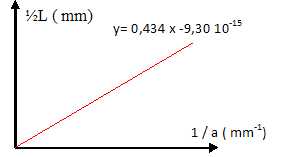
½L =  l D /a ; les distances sont exprimées en mètres.
La pente de la droite est égale à :  lD =0,434 10-6.
l = 0,434 10-6 / 0,70 = 0,62 10-7 m = 620 nm.

19.. Un faisceau laser se propageant dans l'air arrive sous une incidence i1 = 15° à l'interface avec un matériau transparent d'indice de réfraction n. Il subit une déviation de 6°. Que vaut n ? 1,58 ; 0,60 ; 2,48 ; 1,65 ; 0,72.

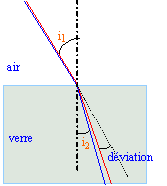
nair sin i1 = n sin i2  avec i2 = 15-6 = 9°.
n = sin 15 / sin 9 =1,65.

 20. On considère une fibre optique à saut d'indice dont le coeur et la gaine possèdent respectivement les indices de réfraction n1 = 1,58 et n2 = 1,52. A partir de quel angle d'incidence I à l'interface coeur/gaine aura-t-on la propagation dans la fibre ?
81,1° ; 73,4° ; 15,8° ; 1,3° ; 74,2°.

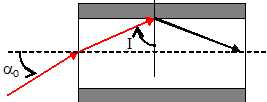
Il y a réflexion totale à l'interface coeur/gaine : n1 sin I = n2 sin 90 ; sin I = n2 / n1 = 1,52 / 1,58 = 0,962 ; I = 74,2°.

.


  

menu