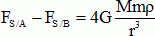Les glaces
d'Europe. Concours agrégation interne 2016
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
La
gravité.
L'interaction gravitationnelle est l'interaction fondamentale la plus
faible mais c'est celle qui structure notre univers. Issac Newton fut
le premier à formuler la loi de gravitation universelle
1. A quelle époque
se situent les travaux d'Issac Newton ?
1642 - 1727.
2. Quels domaines
de la mécanique, connus à l'époque, ont été unifiés par les travaux de
Newton ?
Newton établit les trois lois universelles du mouvement.
Le principe d'inertie, le principe fondamental de la dynamique, le
principe des actions réciproques.
3.
Nommer les quatre interactions fondamentales connues à ce jour et
illustrer le rôle de chacune dans la nature par une courte phrase.
L'interaction gravitationnelle est responsable de la pesanteur, des
marées et des phénomènes astronomiques.
L'interaction électromagnétique est responsable de l'électricité, du
magnétisme, de la lumière.
L'interaction forte est responsable de la cohésion des noyaux atomiques.
L'interaction faible est responsable de la radioactivité ß.
4. Pourquoi est-ce la gravitation
qui structure notre univers ?
L'interaction gravitationnelle est une force toujours attractive. Ces
effets ne sont perceptibles que lorsque les objets sont très massifs,
comme les objets astronomiques.
5. Quelle théorie
du XXième siècle donne aujourd'hui une interprétation plus moderne de
la gravitation ? La décrire par une phrase. Citer le physicien à
l'origine de cette théorie et la date de sa publication.
En 1915, Albert Einstein développe la théorie de la relativité
générale. Elle décrit l'influence sur le mouvement des astres de la
présence de matière et d'énergie. Elle prédit l'expansion de l'univers,
les ondes gravitationnelles et l'existence des trous noirs.
6. Citer les deux
théories de la physique moderne que les travaux de physique théorique
cherchent à unifier.
La physique théorique cherche à unifier la mécanique quantique et la
théorie de la relativité générale.
L'observation
d' Europe au cours des temps.
64 satellites naturels gravitent autour de Jupiter Les quatre
principales lunes furent découvertent par Galilée en 1610. Le 9 juillet
1979, la sonde Voyager 2 envoie une image d'Europe. Son analyse révèle
la présence de glace et laisse suposer la présence d'un océan sous
l'épaisse couche de glace.
En janvier 1610, Galilée lève sa lunette vers le ciel et observe les 4
plus grosses lunes de Jupiter. Cette lunette, de longueur 93,2 cm, est
constituée d'un objectif, lentille plan convexe de 37 mm de diamètre,
diaphragmée à 15 mm et ayant 2 mm d'épaisseur en son centre. Sa
distance focale est de 980 mm. L'oculaire divergent a été perdu, la
lentille mesurait 22 mm de diamètre pour -47,5 mm de distance focale.
Cette lunette grossit 21 fois et présente un champ de 15 ' d'arc.
1. Donner un ordre
de grandeur des limites de la plage de vision
nette d'un oeil humain emmétrope et sa limite de résolution angulaire.
Le champ de l'oeil est l'ensemble des points dont l'image se forme sur
la rétine. Ce sont les objets contenus dans un cône d'angle au sommet
60° dont l'axe et l'axe optique de l'oeil. La tête étant fixe
et les yeux tournant dans les orbites, le champ de vision atteint 30°
de part et d'autre de l'axe optique suivant l'horizontale et 25 °
suivant la verticale.
La résolution de l'oeil normal est d'environ 1,5°, elle dépend de
l'éclairement et du contraste entre l'objet et le fond.
2.
Comment le conservateur du musée de Florence, où est conservée la
lunette de galilée, a-t-il pu reconstituer les informations de
l'oculaire ?
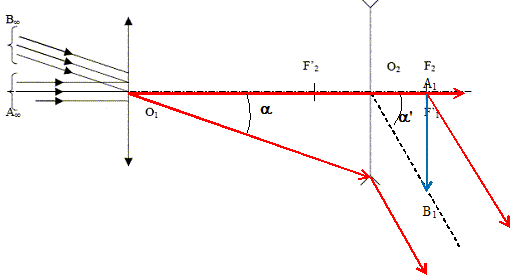
Le système est afocal
; le foyer image de l'objectif et le foyer objet de l'oculaire sont
confondus.
La distance des deux lentilles est égale à 932 mm ; la distance focale
image de l'oculaire vaut : 932-980 =-48 mm. Le diamètre de l'oculaire
vaut : 37-15 = 22 mm.
Grossissement : f'1/|f'2| =980 / 47,5 ~21.
3. Quel est
l'intérêt de diaphragmer la lentille objectif ?
Le diaphragme dose la lumière qui entre dans la lunette ainsi que la
profondeur de champ. De plus le diaphragme supprime les rayons lumineux
trop inclinés sur l'axe optique principal.
4. Vérifier la
cohérence des informations avec la valeur du grossissement.
Grossissement : f'1 / |f'2|
=980 / 47,5 ~21.
5. Comment Galilée
voyait-il Europe à travers sa lunette, comme un objet ponctuel ou un
objet étendu ?
L'image était droite. Le diamètre apparent d'Europe est égal au
diamètre d'Eurpoe divisé par la distance moyenne terre-Jupiter soit :
3122 / (778 106) ~4,0 10-6 rad. Il s'agit donc
d'un objet ponctuel.
|
|
|
6.
Un élève de première S a trouvé sur internet l'affirmation : " la
mesure du champ d'une lunette se fait en dirigeant la lunette immobile
vers une étoile équatoriale, et en chronométrant son temps de passage,
en seconde de temps, dans le champ d'observation. On divise par 4 le
nombre trouvé et on obtient le diamètre angulaire du champ, en minute
d'arc". Cette affirmation est-elle juste ?
L'étoile doit traverser la lunette en passant par son centre.
La terre fait un tour sur elle même, soit 360° en 24 H : 360 / (24*60)
=0,25 ° min-1
ou 1° en 4 minutes ou 15 minutes d'arc en 1 minute ou 15 secondes d'arc
en une seconde ou 0,25 minute d'arc en une seconde ou une minute d'arc
en 4 seconde.
Il suffit de diviser le temps chronométré en seconde par 4 pour obtenir
le diamètre angulaire du champ en minute d'arc.
Le calcul est juste seulement pour une étoile située sur l'équateur
céleste. Pour une étoile de déclinaison non nulle, le temps de passage
varie selon le cosinus de la déclinaison.
7. La résolution de
la caméra numérique de petite ouverture anguaire de Voyager est telle
qu'elle permettrait de lire les gros titres des journaux à 1 km de
distance. Comparer la résolution de cette caméra avec celle de la
lunette de Galilée.
Pouvoir de résolution de l'oeil
normal : 3 10-4 rad soit un détail de 1 cm sur un objet
situé à trente mètres de distance.
Pouvoir de résolution de la lunette de galilée : 3 10-4 / 21
~ 1,410-5 rad, soit un détail de 1 cm sur un objet situé à
0,7 km de distance.
8.
Le télescope Hubble a été capable de détecter la présence de jeyser de
vapeur d'eau sur Europe. Comparer la résolution de cet instrument avec
les deux autres outils précédemment cités.
Des jeysers de 200 km de haut observés depuis une distance de l'ordre
de 778 millions de kilomètres, soit une résolution de 200 / (778 106)
~ 2,6 10-7. ( 100 fois plus grand que celle des instruments
précédents).
|
|
|
|
Quelques
caractéristiques de la trajectoire d'Europe.
1. Justifier qu'en
première approximation, la trajectoire d'Europe puisse être supposée
circulaire autour de Jupiter de rayon DJE. Donner
l'expression de v0 la vitesse sur cette trajectoire
circulaire. Faire l'application numérique.
Demi-grand axe de l'éllipse : 671 100 km ; demi-petit axe
de l'ellipse : 664 860 km.
Demi-grand axe / demi-pretit axe =671100 / 664860 ~1,01.
Ce rapport étant très proche de l'unité, on peut supposer, en
première approximation, une trajectoire circulaire.
v0 =( GMJ / DJE)½ =[6,67 10-11
*1,898 1027 / (668 000 103)]½ =1,38 104
m s-1.
2. Exprimer
l'énergie mécanique Em de ce satellite en orbite circulaire.
La comparer à l'énergie potentielle Ep et à l'énergie
cinétique Ec.
Ec
= ½mEv02 =½mEGMJ
/ DJE. Ep = -mEGMJ
/ DJE ( origine prise à l'infini ).
Em =Ec
+Ep
= -½mEGMJ
/ DJE = ½Ep = -½Ec.
3.
Comparer et commenter la durée du "jour" et de"l'année" sur Europe.
La durée du jour ( révolution sur lui même ) et la durée de l'année (
révolution autour de Jupiter ) sont égaux ( 3,55 jours terrestre ).
Europe présente toujours la même face à Jupiter.
De manière plus
précise, Europe possède une trajectoire élliptique, de foyer O,
d'équation polaire r = p / (1+e cos q),
de paramètre p et d'excentricité e. On suppose qu'à un instant pris
pour origine des temps, la vitesse est orthoradiale de module vb
et la distance à Jupiter minimale.
4. Que dire de l'énergie mécanique Em
?
Europe
est soumis à une force centrale conservative, l'énergie mécanique
d'Europe est constante.
5. Dessiner
l'allure de la trajectoire élliptique en précisant où est Jupiter.
Jupiter est l'un des foyers de l'éllipse.
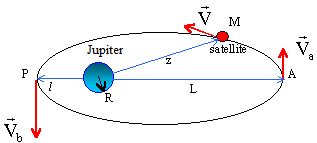
6. Donner les
expressions de rmin = l et rmax = L en fonction
de p et e.
cos q= 1 ; rmin
= p / (1+e) ;cos q= -1 ; rmax
= p / (1-e).
7. Calculer
numériquement p et e.
1+e = p / rmin ; 1-e = p / rmax ; p = 2rmin
rmax (rmin+rmax ).
p = 2*664 860 *671100 /( 664 860 +671 100) =6,68 105 km ; e=
p / rmin -1 =6,68 105 / 664860 -1 = 4,67 10-3.
8. Déterminer
l'expression du champ de gravitation créé par Europe seul à sa surface.
La répartition de masse est supposée à symétrie sphérique. La masse
volumique d'Europe est supposée constante. Le champ de gravitation à la
surface d'Europe créé par Europe seul est GME / RE2.
Etude
de l'eau sur Europe.
1. Commenter la
particularité graphique du diagramme de phase de l'eau, visible sur le
diagramme ci-dessous. L'associer à une autre propriété spécifique
de l'eau.
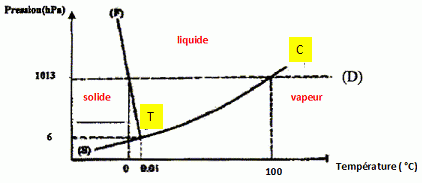
La pente de la droite frontière solide-liquide est négative. Le volume
du solide est supérieur à celui du liquide. La glace flotte sur l'eau
liquide.
2. Quelle pression
est nécessaire pour trouver la présence d'eau liquide ?
La banquise a une épaisseur d'environ 10 km ; la température moyenne de
surface d'Europe est T~100 K.
La pente très forte de la courbe frontière solide-liquide indique qu'il
faut atteindre des pressions très élevées pour observer des changements
significatifs. La pente étant négative, la température de fusion de la
glace diminue lorsque la pression augmente.
3. Cette condition
peut-elle être remplie à la surface d'Europe ? Expliquer les divers
états possibles de l'eau à la surface d'Europe.
La condition n'est pas remplie à la surface d'Europe.
L'atmosphère très ténue d'Europe est constituée de dioxygène ( P = 10-6
Pa). La température en surface est d'environ 100 K.
L'eau existe principalement sous forme de glace et éventuellement sous
forme de quelques traces de vapeur.
Les questions suivantes abordent certains aspects énergétiques d'Europe.
4. On suppose
l'existence d'eau liquide sous la glace. Estimer numériquement la
puissance thermique perdue par diffusion de la chaleur à travers les
glaces d'Europe. L'ordre de grandeur de la conductivité thermique de la
glace est 1 W K-1 m-1.
L'épaisseur de la glace est d'environ 10 km ou 104 m, la
température de l'eau liquide sous la glace est proche de 0°C et la
température de surface est 100 K soit une différence de température de
173 K.
Puissance thermique perdue par diffusion : P = 1* 173 *104
~1,7 106 W.
Une hypothèse avancée pour expliquer l'apport d'énergie nécessaire pour
compenser ces pertes de chaleur par diffusion est la présence d'un
coeur radioactif dans le satellite Europe, à l'image de notre terre.
5. Sachant que la
réaction nucléaire sur terre libère une puissance de 44 TW, et en
supposant que l'énergie nucléaire libérée est proportionnelle à la
masse de l'astre, estimer la puissance produite par le coeur radioactif
d'Europe.
ME / Mterre = 4,8 1022 / 6 1024
= 0,008 ; 44 *0,008 = 0,35 TW = 3,5 1012 W.
Une autre hypothèse qui est évoquée est celle de l'énergie provenant
des forces différentielles de marées.
6. Quelle est
l'origine physique de la force de marée ? Justifier à partir des
caractéristiques du mouvement d'Europe, l'importance des forces de
marées sur Europe.
Les forces de marée sont une conséquence de l'attraction
gravitationnelle
On considère donc deux sphères homogènes
identiques en contact de
masse m et de rayon p telles que la distance de leurs centres A et B
soit AB = 2r. Le
centre de gravité P de l’ensemble des deux sphères tourne à une
distance r du centre S de Saturne. Les points S, A, P et B sont alignés.
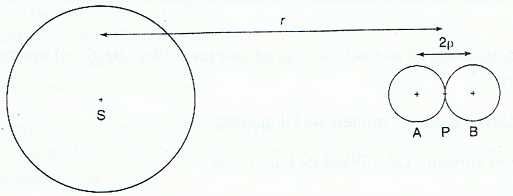
Les deux sphères sont
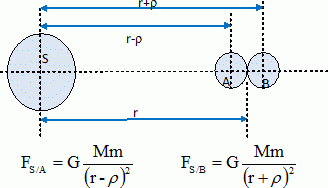
attirées par Saturne par deux forces de valeur FS/A et FS/B.
Les
centres des deux sphères ne se trouvent pas à
la même
distance du centre S de Saturne. Les forces de gravitation exercée par
Saturne sur chaque sphère, sont différentes.
La
différence 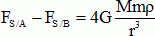 est
encore appelée "force de marées". est
encore appelée "force de marées".
Europe est proche de Jupiter, la masse de Jupiter est très grande
et la profondeur des océans d'eau liquide sur Europe est de l'ordre de
90 km : les forces de marées sont importantes sur Europe.
7. Citer d'autres
processus pouvant intervenir dans le bilan énergétique d'Europe.
Le soleil et Jupiter rayonnent de l'énergie dans l'espace.
Activité volcanique.
|
|