Etude de fonction, équation différentielle. Bts 2016.

Etude de fonction, équation différentielle.
Bts 2016.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Partie A.
Kévin, un apprenti boulanger, décide d’élever des vers de farine pour son club de pêche. Il commence son élevage 7 mois avant l’ouverture de la saison de pêche. Dans un large bac adapté qu’il entrepose à 27°C, il dispose de la farine et 500 vers, il laisse se faire les choses. Il suit l’évolution du nombre de vers et obtient les résultats suivants :

Nombre
de quizaines t_i
0
1
2
3
4
5
6
7
8
9

Nombre
de vers N_i
500
749
1122
1681
2518
3772
5650
8464
12678
18992

y_i
4,17
3,76
3,35
2,92
2,49
2,05
1,58
1,06
0,47
-0,30

1. Kévin se fait la remarque suivante : « chaque quinzaine la population augmente d’environ 50%». Expliquer cette modélisation. Est-elle réaliste sur le long terme ?I
Pendant les 5 premières quizaines, le nombre de vers est multiplié par 1,5.
C'est une suite géométrique de raison q = 1,5.
Au delà l'augmentation du nombre de vers est inférieure, car ces derniers manquent de nourriture.
2. Kévin souhaite connaitre le nombre de vers dont il disposera lors de l’ouverture de la prochaine saison. Il présente ses données à son professeur de mathématiques qui lui propose un nouveau modèle à partir du changement de variable suivant : y_i = ln(33000 /N_i -1).
a. Compléter la troisième ligne du tableau . Arrondir au centième.
b. Déterminer, à l’aide de la calculatrice, une équation de la droite d’ajustement D de y en t par la méthode desmoindres carrés. Arrondir les coefficients au centième.
y = -0,48 t +4,31.
c. Parmi les propositions suivantes quelle est celle qui estime le mieux le nombre de vers pour l’ouverture de la saison de pêche ? Justifier.
33 000 ; 146 000 ; 9 200 ; 30 300.
7 mois = 14 quizaines.
y = -0,48 *14 +4,31 = -2,41.
ln(33000 / N -1) = -2,41 ; 33000 / N -1 = e^-2,41 = 0,0898 ;
N = 33 000 / 1,0898 = 30 280.
3. Maxime, un ami du club, affirme qu’à ce rythme là, le nombre de vers va dépasser 50 000.
Kévin a déterminé que le nombre de vers en fonction du nombre de quinzaines t est donné approximativement par le nombre :
N(t )=33000 / [1+75e^−0,48t].
Kévin peut-il confirmer l’affirmation de Maxime ? Justifier votre réponse.
On ne peut pas atteindre 50 000 vers au bout d'un temps très long. Le terme en exponentielle va tendre vers zéro et le nombre de vers vers 33 000.

Partie B.
De retour à l’école, Kévin apprend que la température de refroidissement du pain à la sortie du four dépend du type de pain et de la température ambiante supposée constante de la pièce dans laquelle il est entreposé.
On note a cette température constante de la pièce, exprimée en degrés Celsius.
Pour t >0, on désigne par y(t ) la température du pain au bout d’un temps t après sa
sortie du four. La durée t est exprimée en heures et la température y(t ) est exprimée en degrés Celsius.
Question préliminaire : parmi les trois courbes suivantes, quelle est celle qui correspond à l’évolution de la température du pain à la sortie du four en fonction du temps ? Argumenter votre réponse.

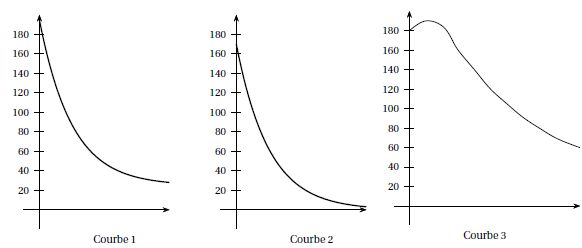
En sortie du four, le pain se refroidit directement et sa température va se stabiliser à la température ambiante soit 20°C ce qui correspond à la courbe 1.
La fonction y vérifie l’équation différentielle :
(E) : y′(t )+6y(t )= 6a.
I. Résolution d’une équation différentielle.
Dans cette partie on considère que le pain est entreposé dans une pièce dont la température constante est a. À la sortie du four, c’est-à-dire à l’instant t = 0, le pain est à une température de 180°C.
1. Déterminer les solutions sur [0 ; +oo[ de l’équation (E₀) : y′ +6y = 0.
y = A exp(-6t) avec A une constante.
2. Soit g la fonction définie sur l’intervalle [0 ; +oo[ par g (t ) = k, où k est une constante réelle dépendant de a. Déterminer k pour que la fonction g soit une solution particulière de l’équation
différentielle (E).
g' = 0, repport dans E : 6 k = 6 a soit k = a.
3. En déduire l’ensemble des solutions de l’équation différentielle (E).
f(t) = A exp(-6t) + a.
4. Démontrer que la fonction h définie sur l’intervalle [0 ; +oo[ par h(t ) = (180− a)e^−6t + a est la solution de (E) correspondant à la condition initiale donnée.
h(0) = 180 = (180-a) e⁰ +a ; cette égalité est vérifiée.
h(t) est la solution de E correspondant aux conditions initiales.

II. Étude d’une fonction.
1. Dans cette question, le pain est entreposé à une température de 28°C.
a. Soit f définie pour tout t >0 par f (t ) = 152e^−6t+28.
Vérifier que f est la solution de l’équation (E) dans le contexte proposé.
f '(t) = 152 *(-6)e^−6t ; repport dans E :
152 *(-6)e^−6t +6 *152e^−6t+6*28 = 6 a avec a = 28.
Cette égalité est vérifiée quelque soit le temps ; f(t) est solution de E.
b. Étudier les variations de f sur l’intervalle [0 ; +oo[.
Le terme en exponentielle est positif, la dérivée est négative sur [0 ; +oo[.
La fonction f(t) est strictement décroissante sur cet intervalle.
c. Déterminer la température µ du pain une demi-heure après la sortie du four. On donnera une valeur approchée de µ à un degré près.
f (0,5 ) = 152e^−6*0,5+28 = 152*0,04979 +28 ~36°C.
d. Le boulanger sort une fournée de pains du four. Déterminer par la méthode de votre choix au bout de quelle durée D le pain sera à une température de 62°C. On donnera une valeur approchée de D à une minute près.
152e^−6t+28 = 62 ; e^−6t = (62-28) / 152 = 0,2237 ; -6t = ln 0,2237 = -1,4975 ;
D = 0,2496 h ou 0,2496 *60 ~15 min.
2. Quelle devrait être la température, au degré près, de la pièce dans laquelle est entreposé le pain afin que ce pain, sorti du four à 16 h, soit à une température de 30°C à 16 h 30 ?
30 =152e^−6*0,5+T ; 30 = 7,56 +T ; T = 22,4°C ~22°C.

.
.

menu