Transformée
de Laplace, série de Fourier, probabilités.
Bts 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Transformée de Laplace.
Une chaîne de traitement de surface est constituée de plusieurs cuves
dont l'une est destinée à réaliser le dégraissage de pièces usinées
dans une solution aqueuse. La température du bain doit être maintenue
entre 75°C et 85 °C. La régulation est assurée par un élément chauffant
dont la puissance doit permettre de compenser les pertes thermiques et
de réaliser la montée en température en un temps déterminé.
Les caractéristiques du système thermique sont les suivantes :
Résistance thermique caractérisant les pertes d'énergie thermique : R =
0,115°C W-1.
k : constante liée à la capacité du système à emmagasiner l'énergie
thermique k = 34,8 J °C-1.
Température de l'air ambiant : qA
= 20°C.
température de la solution aqueuse contenue dans la cuve à l'instant t
: qS(t).
q(t) = qS(t)
-qA.
Une modèlisation du système permet d'établir que pour tout t positif ou
nul, la fonction q
vérifie l'égalité :
q(t)
+ kR dq/dt =
Rf(t) (1).
On note T et F les transformées de Laplace respectives des fonctions q et f.
1. On considère qu'à
l'instant t=0,la température de la solution aqueuse contenue dans la
cuve est égale à celle de l'air ambiant. En appliquant la transformée
de laplace àl'égalité (1) montrer que T(p) = 0,115 / (4,002p+1) F(p).
q(t) +
34,8*0,115 dq/dt
= 0,115 f(t).
q(t) +
4,002 dq/dt
= 0,115 f(t) ; de plus q(0)
= qS(0)
-qA
= 0.
T(p) +4,002 pT(p) = 0,115 F(p) soit T(p)
= 0,115 / (4,002p+1) F(p).
2.
On applique une
puisance échelon de 522 W. On a donc f(t) = 522 U(t).
Donner l'expression de f(p) et en déduire l'expression de T(p).
F(p) = 522 / p ; T(p)
= 0,115 *522/ [p(4,002p+1)].
T(p) ~ 60 / [p(4,002p+1)].
Par la suite, pour simplifier,on prendra T(p) = 60 / [p(4p+1)]
= 15 / [p (p+0,25)].
3.a.
Montrer que
T(p) = 60 / p - 60 / (p+0,25).
T(p) = a / p + b / (p+0,25) avec a et b des constantes.
Réduire au même dénominateur : T(p)=[a(p+0,25) + bp] /
[p (p+0,25)].
T(p)=[(a+b)p+0,25a]
/ [p (p+0,25)].
Identifier : 0,25
a = 15 soit a =60 ; a+b=0 soit b = -a = -60.
3.b. En
déduire que
pour tout t positif ou nul ; q(t) = 60 [1-exp(-0,25t)].
A 60 / p on associe 60 ; à 60/(p+0,25) on associe 60
exp(-0,25t) :
par suite : q(t)
= 60 [1-exp(-0,25t)].
4.a. Déterminer la
limite de q(t)
quand t tend vers l'infini. Justifier.
exp(-0,25t) tend
vers zéro quand
t tend vers l'infini.
q(t)
tend vers 60 quand t tend vers l'infini.
4.b. Que peut-on
déduire pour la courbe représentative de q(t) ?
La droite d'équation y = 60 est asymptote horizontale.
4.c.
Calculer q'(t)
puis étudier les variations de la fonction q.
q'(t)
=
-60 (-0,25)exp(-0,25t) = 15
exp(-0,25t).
q'(t)
est toujours positive ; la fonction q
est croissante
pour tout t positif ou nul.
4.d. Représenter la
fonction q.
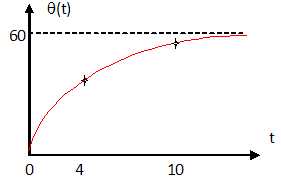
5. Le
technicien estime que, lorsque q(t)
atteint 95 % de sa valeur finale, la température du bain qs(t)
peut être considérée comme constante.
5.a.
Déterminer le temps nécessaire pour que q(t)
atteigne 95 % de sa valeur finale.
0,95*60 =60 [1-exp(-0,25t)].
0,95 = 1-exp(-0,25t)
; 0,05 = exp(-0,25t)
; ln 0,05 = -0,25 t ; t ~ 12 s.
5.b.
Quelle est la température constante autour de laquelle se stabilise la
température du bain ? Le dégraissage serat-il réalisé conformément aux
conditions décrites ci-dessus ?
qs(t)
= 20 +60 = 80°C, valeur conforme aux conditions de température ( [75 ;
85 °C].
|
|
|
Série de
Fourier.
Partie A.
On donne ci-dessous la représentation graphique C d'une fonction f
définie pour tout réel x, paire, périodique depériode T et telle que
pour tout x compris entre 0 et 2p
:
f(x) = x(2p-x).
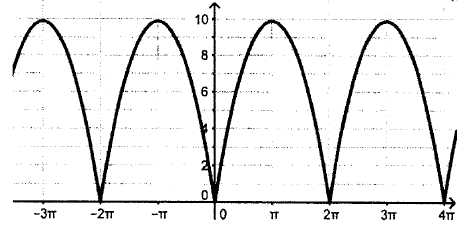
1.
Déterminer T puis w.
Lecture graphique T = 2 p
secondes ; w
= 2p
/ T = 1 rad s-1.
2.
Calculer a0.
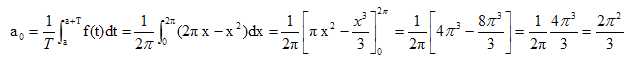
3.
Que valent les coefficients an et bn
pour n supérieur ou égal à 1 ?
La fonction étant paire, les coefficients bn
sont nuls.
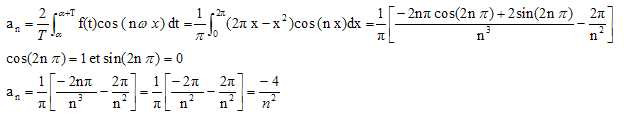
Partie B.
La tension exprimée en volt aux bornes d'une bobine de moteur pas à pas
dépend du temps t exprimé en seconde. Elle est modélisée par la
fonction u impaire, périodique de période T = 6, telle que : u(t) = 0
si t appartient à [0 ; 1 [ ; 2 si t appartient à [1 ; 2 [ ; 0 si t
appartient à [2 ; 3 ].
1.
Tracer la courbe C représentative de u sur l'intervalle [-6 ; 6].
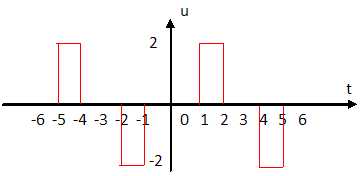
2.
Déterminer la
valeur moyenne de cette tension sur un intervalle de longueur T.
L'aire négative compense l'aire positive ; la valeur moyenne de cette
tension est nulle..
3.
Calculer la valeur de Ueff puis donner une
valeur arrondie à 10-2 près.
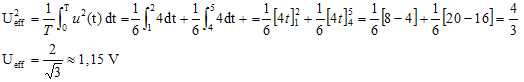
Partie C.
On s'intéresse à une fonction définie pour tout réel t , périodique de
période 2 p
et développable en série de Fourier. On donne son développement :
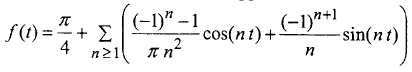
1. Quelle
est la valeur du coefficient a0 du développement
en série de Fourier de f ?
a0
=
p
/ 4.
Exprimer en fonction de n les coefficients an et
bn pour n entier supérieur ou égal à 1.
Si n est pair : an = 0 ; si n est impair an
= -2 / (pn2).
Si
n est pair : bn = -1 /n ; si n est impair bn
= 1 /n.
2. Soit SN(t)
la somme partielle de rang N ( N supérieur ou égal à 1 ) de la série de
Fourier. Ecrire S2(t).
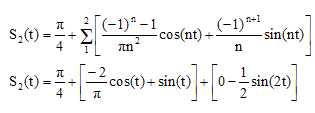
3 Parmi les spectres
d'amplitude ci-dessous quel est celui associé à f ? Expliquer.
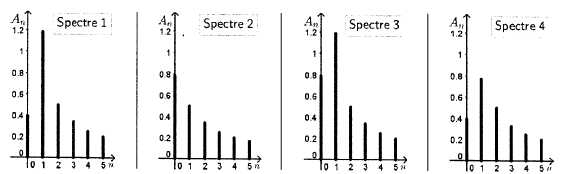
A0 = |a0| =3,14 / 4 ~0,8.
( 1 et 4 ne conviennent pas ).
A1 = (a12
+b12)½
=(4/p2
+1)½ ~1,2. Donc spectre 3.
|
|
|
|
Probabilités.
Partie A. 1,5 % des cellules fabriquées présenteront un défaut et seront inutilisables.
En sortie de production, on forme des lots de 75 cellules. La
production étant très importante, on peut assimiler la constitution
d'un lot de 75 cellules à 75 tirages indépendants avec remise. On note
X la variable aléatoire qui associe à chaque lot de 75 cellules le
nombre de cellules inutilisables qu'il contient.
1. Justifier que X suit une loi binomiale dont on précisera les paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 75. La
probabilité qu'une cellule soit non conforme est constante p = 0,015.
La probabilité qu'une cellule soit conforme est q = 0,985.
X suit la loi binomiale de paramètre n = 75 et p = 0,015.
2. Quelle est la probabilité qu'un lot ne contienne aucune cellule inutilisable ?
p(X=0)=C075 q75 p0 =0,98575 =0,322.
3. Un panneau est
constitué de 72 cellules. Quelle est la probabilité d'avoir
suffisamment de cellules sans défaut dans un seul lot pour pouvoir
fabriquer un panneau ?
Il faut calculer P(X <= 3) = P(X=0) + P(X=1) + P(X=2) +P(X=3)..
p(X=1)=C175 q74 p1 =75 *0,98574 *0,015=0,3676.
p(X=2)=C275 q73 p2 =75*74 / 2 *0,98573 *0,0152=0,2071.
p(X=3)=C375 q72 p3 =75*74*73 / 6 *0,98572 *0,0153=0,07676.
P(X <= 3) =0,322 + 0,3676 +0,2071 + 0,07676 =0,973.
Partie B. Les 72
cellules sont reliées entre elles ( soudure) puis placées sous une
vitre de protection et insérées dans un cadre en aluminium. A la
réception des panneaux, l'installateur constate que certains panneaux
présentent des défauts qui peuvent être de deux types, des défauts
électriques et des défauts de structure.
Une étude statistique a permis d'établir que 2 % des 500 panneaux reçus
avaient un défaut électrique, que 1 % avaient un défaut de structure et
que parmi les panneaux présentant un défaut de structure, 40 % avaient
un défaut électrique.
On choisit au hasard un panneau :
On appelle E l'évenement " le panneau présente un défaut électrique".
On appelle S l'évenement " le panneau présente un défaut de structure".
1. Compléter le tableau d'effectifs suivant.
500 *0,02 = 10 panneaux ont un défaut électrique.
500 *0,01 = 5 ont un défaut de structure.
5*0,4 = 2 ont les deux défauts.
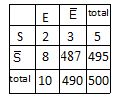
2. Quelle est la probabilité qu'un panneau pris au hasard parmi ceux livrés ne présente aucun défaut ?
487 / 500=0,974.
3. Les évenement E et S sont-ils indépendants ? Expliquer.
Les évenements ne sont pas indépendants.
pE(S) = 2/10 = 0,20 et p(S) = 5/500 = 0,01.
Pour deux évenements indépendants, ces nombres seraient les mêmes.
Partie C.
Dix de ces panneauw sont installés sur le toit d'une maison. On désigne
par Y la variable aléatoire qui, à chaque journée, associe la
production électrique ( kWh). La loi Y suit la loi normale de paramètre
µ=9 et s =3.
1. Quelle est la probabilité que la production journalière soit comprise entre 6 et 12 kWh ?
t =(12-9) / 3 = 1 ; les tables donnent P(1) = 0,841 3.
La probabilité cherchée est : 1-2(1-0,841 3) ~0,683.
2. Parmi les trois fonctions de densités de probabilité représentées ci-dessous, laquelle peut être celle de la loi Y ? Justifier.
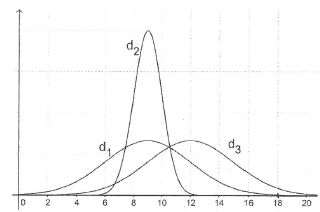
d3 n'étant pas centrée sur 9, ne convient pas.
d2 ne convient pas : les valeurs comprises entre 6 et 12
correspondent à presque 100 %, alors qu'à la question précédente, on a
trouvé 68 %.
d1 convient.
3. Les occupants de la maison consomment en moyenne 10 kWh par jour ( hors chauffage et eau chaude ).
a. Quelle est la probabilité que la production journalière des panneaux soit supérieure à la consommation quotidienne ?
t = (10-9) /3 ~0,333. Les tables donnent P(0,333) ~ 0,63.
Probabilité que la production soit supérieure à 10 kWh par jour : 1-0,63 ~ 0,37.
b. Quelle devrait être la consommation moyenne quotidienne pour que cette probabilité soit d'environ 90% ?
Les tables donnent t ~1,28.
1,28 = (9-x) / 3 ; x ~5,2 kWh j-1.
|
|