Une station de
ski, bac Sti2d 09 / 2016
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Partie A :
l’enneigement des pistes (6 points)
Dès les années 70, les stations de sport d’hiver françaises se sont
équipées pour la production de neige artificielle afin de pallier les
éventuels défauts de précipitation qui peuvent intervenir au cours
d’une saison. Les aménagements consistent le plus souvent à créer une
retenue d’eau en altitude afin d’alimenter des canons à neige disposés
le long des pistes.
Cette partie est constituée d’un questionnaire à réponses ouvertes
courtes.
Pour chacune des questions, plusieurs réponses ou affirmations sont
proposées. Une seule d’entre elles est exacte. Une réponse fausse et
une absence de réponse seront évaluées de la même façon.
Afin
de remplir la retenue d’eau du Morond de la station de ski de Métabief,
l’eau est acheminée par une canalisation depuis la rivière « la
Jougnena ». Ce remplissage nécessite l’utilisation d’une pompe de
relevage adaptée à la différence d’altitude et au débit souhaité.
A.1.1. Quel est le
volume d’eau, exprimé en milliers de mètres cubes, contenu dans la
retenue du col du Morond le 10 décembre 2013 ?
Capacité de la retenue d’eau au sommet du col du Moron :103 000 m3 ;
Depuis le 26 novembre 2013, la pompe est en marche 24 h sur 24 pour
faire grimper une partie de l'eau de « la Jougnena » située à 830 m
d’altitude jusqu'au sommet du Morond à 1350 m, et ainsi alimenter
prochainement les canons à neige de la station.
Ces premiers mètres cubes s'accumulent à raison d'un débit moyen de 100
m3 par heure.
14 jours de pompage soit 14*24 = 336 heures.
Volume d'eau pompé : 336 * 100=33600 m3 ou environ 34 milliers de m3.
Réponse d.
A.1.2.
Quel volume de neige, exprimé en milliers de mètres cubes, est
susceptible d’être produit avec l’eau accumulée au 10 décembre 2013 ?
Un mètre cube d’eau est nécessaire à la fabrication de deux mètres
cubes de neige.
68 milliers de m3.
Réponse b.
A.1.3. Quelle est alors la hauteur
approximative de neige susceptible d’être produite par les canons à
neige ?
La neige artificielle couvrira environ 35 hectares soit 35 104
m2.
68000 / (35 104) ~0,19 m = 19 cm. Réponse d.
A.1.4.
On donne la différence d'altitude entre la rivière et le lac de retenue
: 520 m. Quelle est la valeur de la différence de pression DP de l’eau dans la
canalisation entre la station de pompage et la retenue du col du
Morond, en l’absence de débit ?
Théorème fondamental de l’hydrostatique : DP = rgDh = 1000 *10*520=5,2 106
Pa= 52 bar.
Réponse b.
A.1.5.
Quel est le coût approximatif, exprimé en milliers d’euros, généré par
le fonctionnement de la pompe de relevage de puissance P = 325 kW,
permettant de remplir complètement la retenue d’eau du col du Morond ?
L’énergie électrique E (en kW.h) consommée par un appareil est égale au
produit de sa puissance P (en kW) par la durée Dt (en h) de fonctionnement :
Volume de la retenue : 103 000 m3 soit 1030 heures de
pompage.
E = P.Dt
=325 *1030=334 750 kWh.
1 kWh coûte environ 0,10 € soit environ 33 milliers d'euros. Réponse b.
Un
canon à neige est un dispositif permettant de fabriquer de la neige. Le
principe est de projeter un mélange d'air comprimé et d'eau par temps
suffisamment froid. Il existe plusieurs types de canons à neige.
Certains d’entre eux disposent de gicleurs à section variable.
A.2.1. Quelle est
la surface d’ouverture du gicleur d’éjection d’eau lorsque la
température extérieure est de -10°C ?
Débit de l'eau 34 m3 h-1 ou 34 / 3600 =
9,44 10-3 m3 s-1.
Vitesse de l'eau en sortie : v = 90 m s-1.
Surface d'ouverture du gicleur : 9,44 10-3 / 90 ~1,0 10-4 m2.
Réponse b.
A.2.2. Quelle est
alors la vitesse d’écoulement de l’eau dans la conduite d’alimentation
du canon à neige, conduite de diamètre 60 mm ?
Section de la conduite : pD2/4
= 3,14 *0,0602 /4 =2,83 10-3 m2.
Conservation du débit : 1,0 10-4 *90 = 2,83 10-3
v ; v ~3,3 m s-1. Réponse a.
À la sortie
d’un canon
à neige, un mélange froid d’air et d’eau est expulsé dans l’atmosphère.
Le phénomène physique de nucléation conduit alors à la formation d’un
flocon : c’est la production de neige de culture.
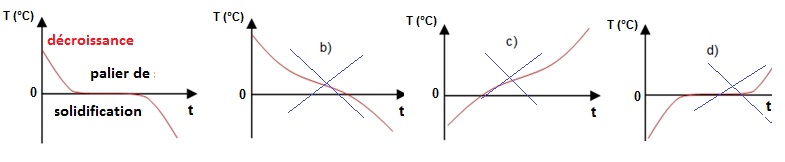
A.2.3. Parmi les
représentations graphiques suivantes, quelle est celle qui correspond à
la solidification de l’eau pure à pression atmosphérique normale ? Réponse a.
|
|
|
Partie B.
corrosion des
canalisations (5 points)
Le transport de l’eau entre l’usine de pompage de l’eau de « la
Jougnena » et la retenue d’eau du Morond se fait par une canalisation
en fonte. La fonte est un alliage de fer et de carbone.
La corrosion est l’un des principaux processus qui contribuent à la
rupture de ce type de canalisation.
Elle met en jeu les couples oxydant/réducteur suivants :
O2(aq) / HO- (aq) et Fe2+(aq) / Fe(s).
La demi-équation électronique associée au couple O2(aq) / HO-
(aq) s’écrit :
O2(g) + 4 e- + 2 H2O(l) = 4 HO-(aq).
B.1. La corrosion
électrochimique
B.1.1. Identifier
les réactifs qui interviennent dans le processus de corrosion.
Le fer, le dioxygène et l'eau.
B.1.2. Écrire la
demi-équation électronique correspondant au couple Fe2+(aq)
/ Fe(s).
Fe(s) = Fe2+aq + 2e-.
B.1.3. Écrire
l’équation de la réaction modélisant la transformation chimique ayant
lieu lors de la corrosion du fer.
O2(g) + 2Fe(s) + 2 H2O(l)
= 4 HO-(aq)+2Fe2+aq.
B.1.4. En utilisant l’annexe B1,
justifier le choix du revêtement extérieur de la canalisation en fonte.
Alliage de zinc aluminium : ces deux métaux sont plus réducteurs que le
fer ; ils s'oxydent à la place du fer et ce dernier est protégé.
B.2. La corrosion acide
L’intérieur des canalisations est recouvert d’un mortier de béton.
La carbonatation du ciment contenu dans le mortier est à l’origine de
la corrosion des canalisations en fonte.
La carbonatation est une réaction lente entre le dioxyde de carbone
présent dans l’eau, se comportant comme un acide, et le ciment
principalement constitué d'une base, l’hydroxyde de calcium.
B.2.1. Donner la
définition d’une base.
Une base est une espèce susceptible de gagner un proton H+.
B.2.2. Justifier la
limitation de la concentration massique en dioxyde de carbone de l’eau
transportée par la canalisation.
Destruction du ciment basique par une trop forte concentration en
dioxyde de carbone acide.
B.2.3. Les
résultats d’une analyse effectuée sur l’eau transportée indiquent une
concentration en ions oxonium H3O+ de 5,0.10-8
mol.L-1 ainsi qu’une concentration en dioxyde de carbone de
2,8.10-4 mol.L-1.
La canalisation est-elle adaptée au transport de cette eau ? Justifier.
pH = - log (5,0 10-8) =7,3 :
Masse de dioxyde de carbone par litre d'eau : 2,8 10-4 *44 =
0,012 g/L ou 12 mg/L.
Pour ce type de canalisation, le pH doit être supérieur à 5,5 et la
teneur en CO2 inférieure à 15 mg/L. Cette canalisation
convient.
|
|
|
|
Partie C
: étude d’une remontée mécanique (5 points)
C.1. Débit de
skieurs
En 1988, la station d’Albiez s’est dotée d’une nouvelle remontée
mécanique de type télésiège.
C.1.1. En supposant
qu’elle est constante, montrer que la vitesse d’une nacelle, appelée
vitesse d’exploitation, est de 2,3 m.s-1.
Longueur de la remontée L = 1590 m ; durée de la montée : 11 min 30 s.
v = 1590 / (11 *60 +30)=2,3 m s-1.
C.1.2. En supposant
que la longueur du câble est le double de la longueur de la remontée,
déterminer le nombre moyen de rotations effectuées par une nacelle en
une heure.
Distance parcourue par la nacelle en une rotation : 2*1590 = 3180 m.
Durée de la rotation : 3180 / 2,3 =1,38 103 s ;
Nombre de rotation par heure : 3600 / 1380 ~2,6.
C.1.3. À partir de
la question précédente, montrer que le débit horaire annoncé par le
constructeur est légèrement surestimé.
145 nacelles de capacité 4 personnes soit : 145*4*2,6 = 1510 personnes
par heure.
Cette valeur est inférieure au débit annoncé, 1600 personne / heure.
C.2. Étude
énergétique
La remontée mécanique fonctionne grâce à un moteur électrique qui
entraîne la poulie de la station d’arrivée.
L’énergie apportée par le moteur à la poulie doit servir simultanément :
- à mettre les skieurs en mouvement lors de l’embarquement dans la
nacelle ;
- à élever leur altitude de la station de départ à celle d’arrivée ;
- à compenser les divers frottements.
En supposant que l’énergie à fournir pour la remontée des nacelles est
compensée par celle fournie par les nacelles qui descendent, on
s’intéressera uniquement à la remontée des skieurs.
C.2.1. Calculer la
valeur de l’énergie cinétique d’un skieur de masse m = 70 kg, installé
sur une nacelle, supposé en mouvement de translation uniforme à la
vitesse de 2,3 m.s-1.
Ec = ½mv2 = 0,5 *75 *2,32 = 1,98 102
~2,0 102 J.
C.2.2. Calculer la
variation d’énergie potentielle de pesanteur de ce skieur quand il
effectue une remontée.
DEp
= mgDh = 75 *10
*(2060-1534)=3,94 105 ~3,9
105 J.
C.2.3. Montrer que
la variation d’énergie cinétique d’un skieur est négligeable devant sa
variation d’énergie potentielle de pesanteur lorsqu’il effectue une
remontée.
3,9 105 / 200 ~2000, la variation d'énergie potentielle est
égale à 2000 fois l'énergie cinétique.
On supposera que le skieur est immobile par rapport au sol juste avant
l’embarquement et immobile par rapport à la nacelle quand il la quitte.
C.2.4. En supposant
que l’énergie dissipée par les frottements est également négligeable
devant l’énergie potentielle de pesanteur, montrer que l’énergie à
fournir au télésiège en une heure de fonctionnement est de l’ordre de
6.108 J si le débit horaire est de 1600 personnes par heure.
3,94 105 *1600 = 6,3 108 J.
C.2.5. En déduire
la puissance mécanique moyenne que doit fournir la poulie de la station
d’arrivée au télésiège.
6,3 108 / 3600 =1,75 105 ~1,8 105 W. ( 1,8 102 kW)
|
Le
moteur entraine la poulie de la station d’arrivée par l’intermédiaire
d’un réducteur mécanique, qui fonctionne comme un engrenage.
C.2.6. Indiquer sur
votre copie la nature de la puissance non identifiée sur la chaîne
énergétique.
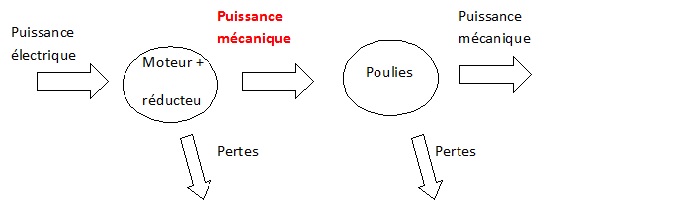
C.2.7. On rappelle
que la puissance électrique du moteur vaut 381 kW. Calculer le
rendement de la chaîne énergétique lorsque le télésiège fonctionne au
maximum de ses capacités.
Puissance mécanique
/ Puissance électrique = 175 / 381 ~0,46 ( 46 %).
Partie D : une
descente chronométrée (4 points)
Un skieur s’élance sur une piste supposée rectiligne.
D.1. Le début de la descente.
Au début de la descente, on suppose que les frottements qui s’exercent
sur le skieur sont négligeables par rapport aux autres forces qu’il
subit.
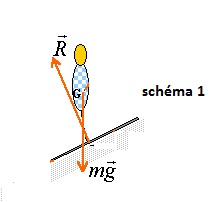
D.1.1. Choisir le
schéma
traduisant correctement les forces qui s’exercent sur le skieur
immédiatement après son départ. Justifier.
D.1.2. Nommer
chacune des forces représentées sur le schéma retenu.
Le skieur est soumis à son poids et à l'action du plan, perpendiculaire
au plan, les frottements étant négligés.
D.1.3.
L’accéléromètre qui équipe son smartphone lui indique une valeur de 3,9
m.s-2.
En déduire la valeur de la résultante des forces qui s’exercent sur le
skieur sachant que sa masse est de 70 kg.
m a = 70 *3,9 =273 ~2,7 102 N.
D.2. L’enregistrement de la descente.
En exploitant le film de sa descente, le skieur obtient la courbe de
l’évolution de sa vitesse au cours du temps représentée.
D.2.1. En tenant
compte de sa vitesse initiale, déterminer la distance
parcourue par le skieur après 2,0 secondes de descente. Préciser le
modèle de mouvement choisi.
Pendant les 2 premières secondes de la descente le mouvement est
rectiligne uniformément accéléré. La vitesse initiale du skieur est v0
= 2 m /s.
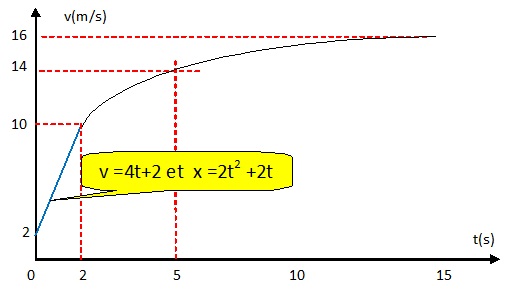
Distance parcourue : 2 * 22 +2*2 = 12 m.
Dans une position donnée, la valeur de la force de frottement f
exercée par l’air sur le skieur peut s’exprimer par la relation :
f=K×v2 où K est une constante et v la valeur de la vitesse
du skieur.
D.2.2. À partir de
l’expression de la force de frottement, proposer une unité de K
utilisant les unités kg, m et s.
K est une force divisée par une vitesse au carré.
Une force est une masse (kg) fois une accélération ( m s-2)
K s'exprime en : kg m s-2 / (m2 s-2)
soit en kg m-1.
D.2.3. Quelle est
la valeur de l’accélération du skieur après 15 s de descente ?
Justifier.
La valeur de la vitesse étant constante, le mouvement est rectiligne
uniforme. L'accélération est nulle.
D.2.4. En
négligeant les autres frottements, calculer la valeur de la
force de frottement exercée par l’air sur le skieur, après 15 s de
descente.
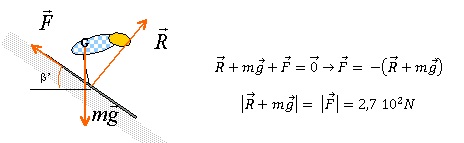
.
|
|