Acide aminé,
dosage acido-basique, pression débit.
Bac ST2S Antilles 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Exercice
1 : Antibiotique et molécule associée.
Lors d’une consultation chez un médecin et diverses analyses, il est
diagnostiqué que la petite Noémie est atteinte d’une infection des
voies respiratoires ; l’origine de cette infection est bactérienne. La
patiente a trois ans et possède une masse de douze kilogrammes.
1. Etude des substances actives du
médicament.
Arrivé à son domicile, le père de Noémie prépare la solution buvable en
versant la quantité d’eau indiquée sur la notice.
1.1. Nommer la
molécule antibiotique contenue dans la solution.
L’amoxicilline.
1.2. Expliquer la
stratégie qui consiste à associer l’amoxicilline à l’acide clavulanique.
L’acide clavulanique
inhibe les bêta-lactamases produites par des bactéries à Gram positif
et à Gram négatif.
L’amoxicilline se
montre actif sur un nombre important de bactéries dont celles
résistantes aux antibiotiques par sécrétion de bêta-lactamases de type
pénicillinases.
2. Etude du dosage d’une substance
active.
2.1. Montrer que le
volume correspondant à une dose-graduation est égal à 0,27 mL.
10,5 g de poudre permettent la fabrication de 60 mL de suspension
buvable.
Un flacon contient 224 doses-graduations.
60 / 224 =0,268 ~ 0,27 mL.
2.2. Calculer le
volume de solution correspondant à une prise pour Noémie.
1 dose correspondant à 1 kg de masse de l’enfant, donc 12 doses.
Soit 12 *0,268 =3,21 ~ 3,2 mL.
2.3. Montrer que la
masse d’amoxicilline absorbée par l’enfant à chaque prise est égale à
0,324 g.
1 mL de solution contient 0,100 g d'amoxicilline.
3,21 *0,100 = 0,321 ~0,32 g.
2.4. Noémie serait
en surdosage si elle consommait plus de trois grammes d’amoxicilline
par jour.
Préciser si Noémie est en surdosage. Justifier la réponse apportée.
Trois prises par jour sont nécessaires soit 0,321*3 ~0,96 g.
Noémie n'est pas en surdosage.
2.5. Expliquer la
phrase suivante :
Attention, cette seringue pour administration orale ne doit pas être
utilisée pour administrer un autre médicament car la graduation de
cette seringue est spécifique de ce produit.
La seringue ne paut pas servir à mesurer un volume en mL, car elle est
graduée en kg de masse corporelle de l'enfant.
3. Hydrolyse de
l’amoxicilline
On a entouré cinq groupes caractéristiques de l’amoxicilline.
3.1. Compléter
l’annexe en indiquant le nom de chacun de ces cinq groupes
caractéristiques.
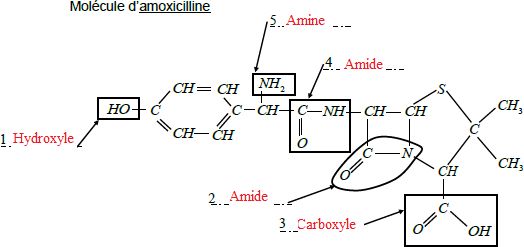
Lors de l’hydrolyse de l’amoxicilline la molécule subit une cassure au
niveau du groupe portant le
numéro 4. Pour simplifier, on utilisera l’écriture suivante pour
représenter l’amoxicilline. L’équation de la réaction d’hydrolyse
s’écrit :
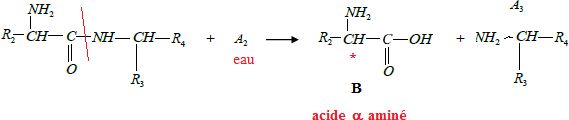
3.2.
Nommer la molécule A2.
3.3. Ecrire la
formule semi-développée de la molécule notée A3.
3.4.
Préciser le nom de la famille à laquelle appartient la molécule
ci-dessous (nommée B)
obtenue lors de l’hydrolyse.
3.5.
Reproduire la molécule B sur la copie et repérer avec un astérisque (*)
le carbone
asymétrique.
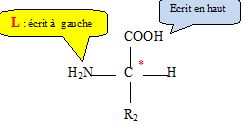
3.6. En utilisant
la représentation de Fischer, donner la configuration L de la molécule
B.
|
|
|
Exercice
2 : Dosage acido-basique.
On souhaite déterminer la concentration de l’acide clavulanique dans la
solution buvable.
Pour simplifier, on suppose que seul l’acide clavulanique a des
propriétés acido-basiques dans la
solution buvable.
1. Etude
acido-basique de l’acide clavulanique
Pour simplifier, l’acide clavulanique sera noté R5 COOH.
1.1. Entourer
l’atome d’hydrogène concerné par les propriétés acidobasiques de
l’acide clavulanique.
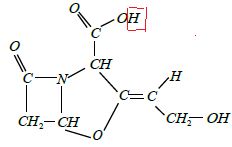
1.2. Ecrire la
formule de la base conjuguée de l’acide clavulanique appelée ion
clavulanate.
R5 COO-.
Le pKa de ce
couple vaut 2,8. Le pH de la solution buvable est égal à 6.
1.3. Représenter le
diagramme de prédominance des espèces acide clavulanique et ion
clavulanate en solution aqueuse.
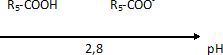
1.4. Identifier
l’espèce prédominante dans la solution buvable. Justifier la réponse.
A pH = 6, supérieur à pKa, la forme R5-COO-
prédomine.
2. Dosage
pH-métrique
On prélève un volume Va de solution buvable, égal à 20,0 mL.
2.1. Choisir la
verrerie qu’il convient d’utiliser pour ce prélèvement.
Un volume précis est mesuré à l'aide d'une pipette jaugée de 20,0 mL
dans ce cas.
On procède au dosage par suivi pHmétrique en ajoutant progressivement
une solution d’hydroxyde de potassium à la solution prélevée. La
solution titrante d’hydroxyde de potassium K+aq +HO-aq
a une concentration molaire Cb égale à 1,00x10-1
mol.L-1.
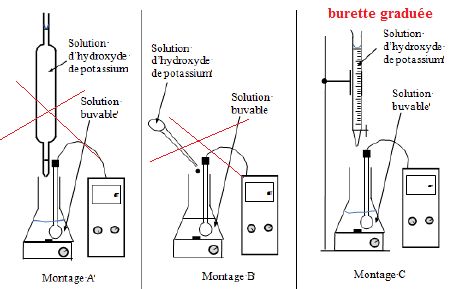
2.2. Parmi les
schémas proposés ci-dessous, choisir le dispositif adapté pour cette
manipulation.
Justifier le choix.
|
|
|
|
Afin
d’étalonner le pH-mètre, on utilise deux solutions tampon. La première
a un pH = 4 et la seconde a un pH = 7.
2.3. Citer une
propriété de ces solutions.
Une solution tampon modère les variations de pH suite à l'ajout modérée
d'acide ou de base forte, ou à une dilution modérée.
3. Exploitation du
graphique
Le suivi pH-métrique du dosage permet de tracer la courbe représentant
l’évolution du pH du mélange réactionnel en fonction du volume Vb
de solution d’hydroxyde de sodium ajouté.
3.1. Représenter
l’allure de la courbe du pH en fonction de Vb. Préciser les
grandeurs représentées sur chaque axe du graphique.
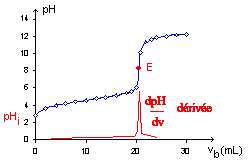
Le volume équivalent notéVbe
est égal à 12,5 mL. L’équation de la réaction chimique du dosage est :
R5 COOH + HO- --> R5COO-
+H2O.
3.2. Définir
l’équivalence du dosage.
A l'équivalence les quantités de matière des réactifs sont en
proportions stoechiométriques.
3.3. Montrer que la
concentration en acide clavulanique dans la solution buvable est donnée
par
la relation Ca = Cb Vbe / Va.
A l'équivalence, quantités de matière :
d'acide : CaVa
; de base : Cb
Vbe ; CaVa
=Cb Vbe.
3.4. Calculer la
concentration molaire en acide clavulanique.
Ca
=0,100 *12,5 / 20,0 = 0,0625 mol/L.
3.5.
Déterminer la concentration massique notée m C en acide
clavulanique.
Donnée : La masse molaire moléculaire M de cet acide vaut 199,0 g.mol-1.
mC = 0,0625*199 = 12,4 g/L.
3.6. En analysant
le document 1 de l’exercice 1, exploiter l’information utile qui permet
de retrouver rapidement la concentration massique précédente.
Rapport massique amoxicilline / acide clavulanique = 8/1 ;
Quantités pour 1 mL de solution préparée Amoxicilline :100 mg soit 100
g /L.
Par suite : 100 / 8 = 12,5 g/L d'acide
clavulanique.
Exercice 3 :
Administration de la solution buvable.
1. La seringue est
remplie
Après avoir suivi le protocole de fabrication de la solution
d’antibiotique le papa de Noémie a rempli la seringue en tirant sur le
piston. Lorsque la graduation est atteinte, le piston est immobile. La
masse volumique r de
la solution vaut 1,22 g.mL-1. Le volume total V aspiré
tenant compte du poids de l’enfant est égal à 3,2 mL.
1.1. Calculer la
masse de liquide correspondante.
3,2 *1,22 = 3,9 g.
1.2. Montrer que la
valeur du poids du liquide est de 0,038 N.
L’intensité du champ de pesanteur g est égal à 9,8 N.kg-1.
P = mg = 3,9 10-3 *9,8 = 0,038
N.
1.3. Indiquer la
direction et le sens du poids du liquide contenu dans la seringue.
Le poids est dirigé sur la verticale, vers le bas.
1.4. Représenter le poids du liquide au point G. L’échelle est de 1 cm
pour 0,01 N.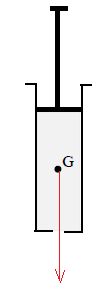
La section S1 du piston en contact avec le liquide est égale
à 0,25 cm2 c’est-à-dire à 2,5x10-5 m2.
La section S2 de l‘orifice de la seringue est égale à 6,3 mm2
c’est-à-dire à 6,3x10-6 m2.
La seringue est placée dans l’air. La pression atmosphérique Patm
vaut 1022 hPa.
1.5. Donner la
relation qui relie la pression P d’un fluide à la force F qu’il exerce
sur une paroi de surface S. On précisera les unités dans le système
international (SI) des différentes grandeurs.
P = F / S avec P en
pascal, F en newton et S en mètre carré.
1.6. Déterminer la
valeur de la force de pression exercée par l’air sur le liquide au
niveau de l’orifice de la seringue. Donnée : 1 hPa = 100 Pa.
F = PS = 1,022 105 *6,3 10-6 = 0,64 N.
La seringue est tenue verticalement, l’orifice étant orienté vers le
bas. On considère que le liquide est soumis uniquement à son poids car
le piston est bloqué.
1.7. À l’aide des
deux résultats numériques précédents, prévoir s’il faut prendre une
précaution particulière pour que la seringue ne se vide pas. Expliquer
la démarche.
Le poids du liquide est très inférieur à la force pressante exercée par
l'air. La seringue ne se vide pas.
|
2. On vide la seringue
Une fois placée l’extrémité de la seringue dans la bouche de sa fille,
le papa pousse sur le piston et éjecte la solution buvable.
Il estime que le liquide est éjecté pendant une durée Dt égale à deux secondes.
2.1. Montrer que le
débit volumique D égal à 1,6 x 10-6 m3.s-1.
Volume du liquide V = 3,2 mL = 3,2 10-6 m3.
D = V / Dt = 3,2
10-6 / 2,0 = 1,6 x 10-6 m3.s-1.
Le débit D d’un fluide à travers une ouverture de section S est égal au
produit de sa vitesse v par la valeur de la section selon la relation :
D = S x v.
2.2. Montrer que la
vitesse d’éjection du liquide v2 est égale à 0,25 m s-1.
v2 =D / S2= 1,6 x 10-6 / (6,3x10-6)
=0,25 m s-1.
2.3. Le liquide est
considéré comme incompressible.
Justifier que l’expression de la vitesse de déplacement du piston notée
v1 est donnée par la relation : v1 = S2
v2 / S1.
Le débit volumique est constant : S2 v2 =v1
S1.
2.4. Calculer v1
et préciser son unité.
v1 =6,3x10-6 *0,25 / (2,5x10-5)
=0,063 m s-1.
2.5. Comparer v1
et v2. Commenter ce résultat.
0,25 / 0,063 ~4.
Pour un fluide incompressible, la vitesse est d'autant plus grande que
la section est plus petite.
|
|