La soie
d'araignée. Bac S
Liban 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
La soie que produisent les araignées pour tisser leurs toiles ou envelopper leurs proies possèdent
des propriétés physico-chimiques si exceptionnelles (finesse, régularité, élasticité, solidité,
imputrescibilité, etc…) qu’elle est devenue un sujet d’étude pour de nombreux scientifiques. Cet
exercice aborde plusieurs aspects de la soie d’araignée considérée comme un matériau d’avenir
1. Composition de la soie d’araignée.
La soie d’araignée est essentiellement composée de fibroïne, une molécule constituée de
plusieurs centaines d’acides aminés reliés les uns aux autres par des liaisons peptidiques. Les
deux principaux acides aminés présents dans la fibroïne sont la glycine (40 % environ) et l'alanine
(25-30 % environ) dont les formules semi-développées sont indiquées ci-dessous.
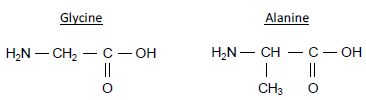 Selon l’enchaînement des différents acides aminés au sein de la macromolécule de fibroïne, cette protéine peut adopter deux structures géométriques tridimensionnelles différentes : soit une
structure semi-cristalline en feuillets bien ordonnés, soit une structure amorphe inorganisée.
Selon l’enchaînement des différents acides aminés au sein de la macromolécule de fibroïne, cette protéine peut adopter deux structures géométriques tridimensionnelles différentes : soit une
structure semi-cristalline en feuillets bien ordonnés, soit une structure amorphe inorganisée.
La soie d’araignée est donc un matériau dont les propriétés mécaniques découlent de
l’organisation structurale particulière de la molécule de fibroïne :
des régions cristallines expliquent la résistance élevée de la soie
d’araignée tandis que des régions amorphes sont responsables de
son importante élasticité.
1.1. Pourquoi les molécules de glycine et d’alanine appartiennent-elles à la famille des acides aminés ?
La glycine et l'alanine possèdent à la fois le groupe amine NH2 et le groupe carboxyle COOH.
1.2. La molécule de glycine possède-t-elle des stéréoisomères ? Argumenter.
La molécule de glycine ne possède ni atome de carbone asymétrique ni double liaison C=C : elle ne possède pas de stéréoisomère.
1.3. La molécule d’alanine compte deux stéréoisomères
Donner la représentation de Cram de ces deux stéréoisomères, puis justifier le type de relation de
stéréoisomérie qui les lie.
Cette molécule possède un atome de carbone asymétrique ; il existe donc deux énantiomères.
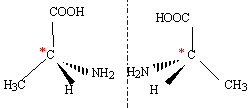
1.4. Après avoir hydrolysé les protéines de la soie d’araignée, on en extrait la glycine et l’alanine.
On réalise ensuite une spectroscopie RMN du proton afin de caractériser leur présence.
Indiquer le nombre de protons équivalents dans chaque molécule et prévoir, en expliquant votre
démarche, le nombre et la multiplicité des signaux observés dans chacun des spectres RMN de la
glycine et de l’alanine, sachant que les atomes d’hydrogène reliés aux atomes d’oxygène et
d’azote n’interviennent pas dans la multiplicité des signaux des atomes d’hydrogène voisins.
Glycine : proton du groupe COOH, singulet.
Protons du groupe CH2, singulet ( l'atome de carbone voisin ne porte aucun proton ).
Protons du groupe NH2, singulet.
Alanine : proton du groupe COOH, singulet.
Protons du groupe méthyle CH3, doublet ( l'atome de carbone voisin porte un seul proton ).
Proton CH : quadruplet ( l'atome de carbone voisin porte trois protons ).
Protons du groupe NH2, singulet.
|
|
|
2. Biomimétisme chimique.
Actuellement, les chimistes cherchent à réaliser des fibres artificielles reproduisant les propriétés
de la soie d’araignée en créant des polypeptides dont la composition et la structure sont les plus
proches possible de celles de la fibroïne. Les polypeptides sont de longues molécules obtenues
par l’assemblage de plusieurs acides aminés La réaction permettant d’assembler deux acides
aminés est appelée « synthèse peptidique ».
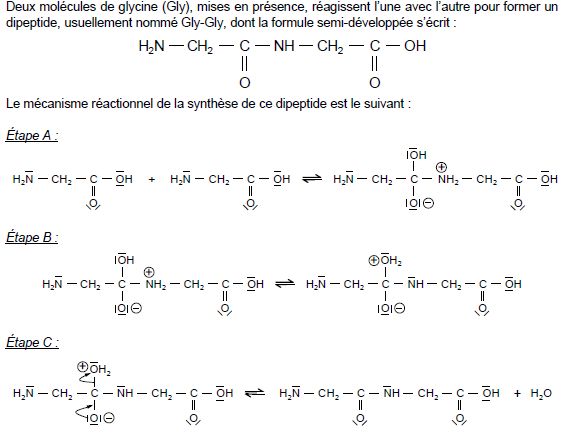
Principe et mécanisme réactionnel d’une synthèse peptidique.
|
|
|
|
Stratégie de synthèse.
Pour synthétiser un dipeptide donné, les chimistes protègent au
préalable les fonctions organiques qui ne doivent pas réagir ensemble,
puis font réagir les fonctions non protégées (synthèse peptidique), et
enfin déprotègent les fonctions n’ayant pas participé à la synthèse En
l’absence de ces précautions, plusieurs dipeptides différents peuvent
être obtenus au terme de la synthèse peptidique.
2.1. Nommer la nouvelle fonction chimique présente dans le dipeptide Gly-Gly.
Fonction peptidique ou amide.
2.2. Analyse du mécanisme réactionnel.
2.2.1. Recopier
l'étape A du mécanisme réactionnel de cette synthèse et la compléter
par le tracé des flèches courbes nécessaires. Justifier précisément
l’orientation de la flèche conduisant à la formation de la liaison.
L'atome d'azote, porteur d'un doublet non liant, est un site nucléophile, donneur d'électrons.
L'atome de carbone du groupe carbonyle est déficitaire en électrons,
l'atome d'oxygène étant plus électronégatif que le carbone. C'est un
site électrophile, accepteur d'électrons.
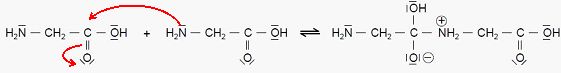
2.2.2.
L’étape B de ce mécanisme réactionnel correspond à une « réaction
acido-basique intramoléculaire ». Justifier cette appellation.
Echange d'un proton entre le groupe OH et le groupe +NH2.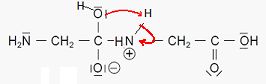
2.2.3. À quelle catégorie de réaction appartient l’étape C de ce mécanisme réactionnel ? Justifier.
A partir d'un seul réactif, on obtient deux produits, dont une molécule d'eau.
Elimination d'une molécule d'eau.
2.3. Combien de
dipeptides différents peut-on, a priori, obtenir par synthèse
peptidique d’un mélange de glycine (Gly) et d’alanine (Ala), sous la
forme d’un unique énantiomère chacun ? Argumenter votre réponse.
On peut obtenir 4 dipeptides :
Le groupe NH2 de la glycine peut réagir avec le groupe COOH d'une autre molécule de glycine pour donner Gly-Gly ;
De même, on obtient Ala-Ala ; Gly-Ala et Ala -Gly.
2.4. La fabrication
de fibres artificielles aussi élastiques et solides que la soie
d’araignée utilise le dipeptide Gly-Ala comme motif de base de la
chaine polypeptidique. La formule topologique de ce dipeptide est la
suivante :
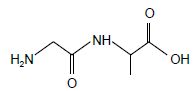
Ce dipeptide étant obtenu par synthèse peptidique en faisant réagir de
la glycine (Gly) et de l’alanine (Ala), préciser la (ou les)
fonction(s) que l’on doit protéger sur chacune de ces deux molécules
pour obtenir uniquement le dipeptide Gly-Ala.
Il faut protéger le groupe COOH de l'alanine et le groupe NH2 de la glycine.
|
3. Détermination du diamètre d’un fil d’araignée.
Un fil d’araignée, de diamètre inconnu noté a, est maintenu en position
verticale et éclairé au moyen d’une source laser rouge de longueur
d'onde l = 615
nm. Le fil est placé à quelques centimètres de la source laser et à une
distance D assez éloignée d’un écran vertical. La figure de diffraction
obtenue à l’écran est caractérisée par une tache centrale de largeur L
et un angle de diffraction noté q.
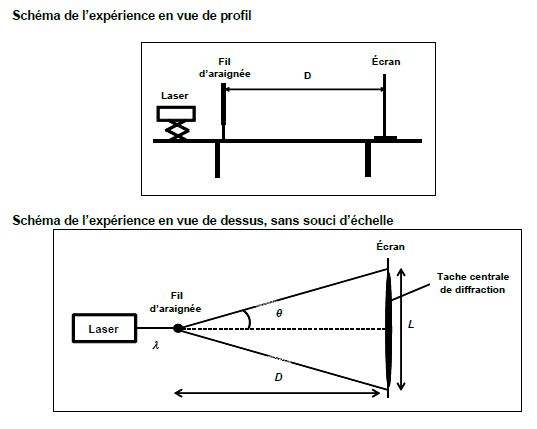
3.1. Quel caractère de la lumière est mis en évidence par l’apparition d’une figure de diffraction ?
La diffraction met en évidence le caractère ondulatoire de la lumière.
3.2. Rappeler l’expression qui lie les grandeurs a, q et l sachant que tan q = q pour les faibles valeurs de q en radian, démontrer que la largeur L de la tache centrale de diffraction admet pour expression littérale : L = 2 lD / a.
D'une part q = l / a, d'autre part tan q ~q = ½L / D. Par suite : L = 2 lD / a.
3.3. Calculer, en m puis en μm, le diamètre a du fil d’araignée analysé sachant que D = 2,00 ± 0,01 m et L = 18,8 ± 0,4 cm.
a = 2 lD / L = 2*615 10-9 *2,00 / 0,188 = 1,31 10-5 m = 13,1 µm.
3.4.
La source lumineuse étant un laser, on fera l’hypothèse que
l’incertitude sur la longueur d’onde peut être négligée par rapport aux
autres incertitudes. L’incertitude absolue U(a) associée à la mesure du
diamètre a du fil d’araignée dépend uniquement des incertitudes
absolues U(D) et U(L) associées aux distances D et L selon la relation
suivante. Exprimer le r 2015ésultat de la mesure expérimentale du diamètre a du fil d’araignée sous la forme d’un encadrement.
( U( a)/a )2 = (U ( L)/L )2 + ( U( D)/D )2 =(0,4/18,8 )2 + ( 0,01/2 )2 ~4,8 10-4 ; U( a)/a ~2,2 10-2. U( a) ~13,1 *2,2 10-2 ~0,3 µm.
a = 13,1 ±0,3 µm.
3.5. Le même fil
d’araignée que celui étudié dans la partie précédente est maintenant
observé et photographié à l’aide d’un microscope optique équipé d’un
appareil photo numérique. Voici le cliché obtenu :
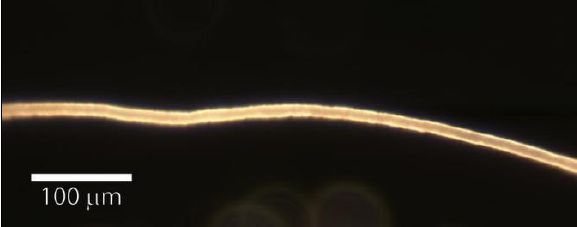 2015 2015
Déterminer le diamètre a
du fil à partir du cliché ci-dessus et donner le résultat assorti de
l’incertitude absolue U(a) associée à cette valeur. Dans cette mesure,
on considère que :
U(a) / a = U(d) / d avec d la valeur mesurée sur la photographie et U(d) l’incertitude absolue associée.
On mesure une épaisseur de 5 mm ±0,3 mm ; 36 mm mesurés correspondent à 100 µm ;
par suite d = 100 *5 /36 ~14 µm et U(d) / d = 0,3 / 5 ~0,06 ; U(a / a = 0,06 ; U(a) = = 14 *0,06 ~1 µm
a = 14 ± 1 µm.
3.6. La mesure par
diffraction du diamètre du fil d’araignée réalisée dans la partie
précédente est-elle cohérente avec la mesure effectuée au microscope
optique ? Détailler la réponse.
Mesure par diffraction : a est compris entre 12,8 µm et 13,4 µm.
Mesure au microscope : a est compris entre 13 µm et 15 µm.
Les deux intervalles se recoupent, les mesures sont cohérentes.
3.7. Quelle méthode est-il préférable d’utiliser pour réaliser cette mesure ? Justifier votre réponse.
La mesure par diffraction est la plus précise ( en augmentant D, on
augmente la précision sur L ), mais plus complexe à mettre en oeuvre.
La mesure au microscope optique est plus rapide, mais nécessite un étalonnage.
4. Élasticité et solidité d’un fil d’araignée.
Dans les forêts
tropicales d’Amérique, la néphile clavipes est l’une des araignées les
plus communes et les plus impressionnantes. Sa toile dépasse souvent un
mètre de diamètre, les fils de soie ont des reflets dorés et collent
fortement. Si par mégarde, vous prenez une telle toile dans le visage
lors d’une sortie nocturne, vous verrez que les fils ne cèdent pas !
Ils sont si résistants que l’on cherche à les utiliser dans la
fabrication de gilets pare-balles. D’après www.futura-sciences.com.
Modèle élastique d’une fibre cylindrique.
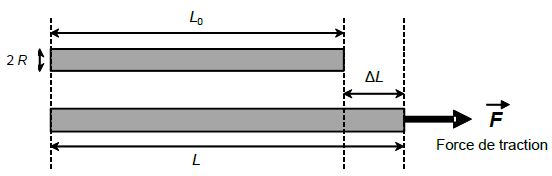
Lorsque l’on soumet une fibre élastique cylindrique de rayon R et de longueur L0
à une force longitudinale de valeur F appelée « force de traction », la
fibre s’allonge et acquiert une nouvelle longueur L > L0. Aux faibles valeurs de F, l’allongement DL = L - L0 de la fibre est proportionnel à la valeur de la force appliquée et satisfait à la relation suivante :
ΔL = FL0 /(EpR2) où E est une constante appelée « module de traction » qui dépend de la nature de la fibre.
4.1. Par une analyse dimensionnelle, vérifier que le module de traction d’une fibre élastique s’exprime en N∙m-2.
E = FL0 /(ΔLpR2) ; L0 /ΔL est sans dimension ; p est sans dimension ; E a la dimension d'une force divisée par une distance au carré.
4.2. On soumet un fil de soie d’araignée néphile clavipes de rayon R = 2,5 μm et de longueur initiale L0
= 6,5 cm à une force de traction de valeur F = 0,03 N Le fil s’allonge
alors jusqu’à atteindre une longueur L = 7,7 cm. Vérifier que ces
valeurs expérimentales sont en accord avec la valeur du module de
traction de la soie de cette araignée 8 109 N m-2.
E = FL0 /(ΔLpR2) = 0,03 *6,5 / (1,3 *3,14 *(2,5 10-6)2) =7,6 10-9 ~8 10-9 N m-2.
4.3.
Expliquer qualitativement comment varie l’élasticité d’une fibre en
fonction de la valeur de son module de traction, puis comparer les
propriétés élastiques d’un fil d’araignée néphile clavipes, d’un
cheveu( E = 10 x 109), du nylon ( E = 3 109) et de la laine( E = 14 109).
L'élasticité d'une fibre est inversement proportionnelle au module de traction E. Plus E est grand, plus la fibre est rigide. Les
propriétés élastiques d’un fil d’araignée néphile clavipes sont
comparables à celles d'un cheveu, supérieure à celles de la laine,
inférieures à celles du nylon.
4.4.
Sachant qu’un fil de soie de néphile clavipes de rayon R = 2,5 μm peut
s’allonger au maximum de 35 % avant de rompre, calculer la masse
maximale que l’on peut suspendre verticalement à un tel fil avant sa
rupture.
ΔL =0,35 L0 = FL0 /(EpR2) ; F = 0,35 EpR2 = 0,35 *8 109 *3,14 *(2,5 10-6)2 = 0,055 N.
Masse correspondante : 0,055 / 9,8 = 5,6 10-3 kg ~ 6 g.
|
|