Vol zéro G. Bac S
Liban 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Au
printemps 2015, l’airbus A310 Zéro-G a réalisé ses premiers vols
scientifiques. Exploité par une filiale du Centre National d’Études
Spatiales (CNES), cet avion permet de simuler des conditions
d’apesanteur en décrivant des trajectoires paraboliques. Les
scientifiques peuvent ainsi mener des expériences sans avoir recours
aux missions spatiales.
Document 1 : Trajectoire parabolique de l’A310 Zéro-G
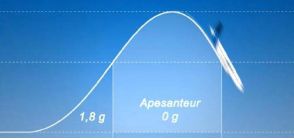
Pour que les passagers et le matériel embarqués dans l'Airbus A310
Zéro-G soient en apesanteur dans le référentiel de l'avion, et qu'ils
se mettent à y "flotter", il faut que l'avion soit en chute libre.
Dans le référentiel terrestre, un corps est en chute libre lorsque la
seule force qui s'exerce sur lui est le poids. Comment mettre l'avion
en condition de "chute libre", peut-on se demander. Rien de plus
"simple". Il suffit que le pilote de l'avion arrive à suivre la bonne
trajectoire parabolique.
Extrait d’un article de presse.
Document 2 : Caractéristiques du vol parabolique
Angle par rapport à l'horizontale au début de la parabole 47°
Altitude au départ et à la fin de la parabole 7 600 m
Vitesse au début de la parabole 527 km.h-1
Altitude au sommet de la parabole 8 200 m
Vitesse au sommet de la parabole 355 km.h-1
Durée d'apesanteur (0 g) 22 s.
Données :
- masse de l’airbus A310 Zéro-G et de son équipement : m = 1,5×105 kg ;
- constante de gravitation universelle : G = 6,67×10-11 m3.kg-1.s-2;
- intensité du champ de pesanteur à la surface de la Terre : g = 9,81 N.kg-1 ;
- masse de la Terre : M = 6,02×1024 kg ;
- rayon de la Terre : R = 6,38×106 m.
On se place dans le référentiel terrestre considéré comme galiléen sur la durée d’une parabole.
1. Étude du mouvement de chute libre.
On souhaite vérifier, par des considérations énergétiques, que la
trajectoire suivie par l’avion est modélisable par une chute libre.
1.1. Rappeler la condition que doit vérifier l’énergie mécanique d’un système lorsqu’il est en chute libre.
Un système en chute libre n'est soumis qu'à son poids ; le poids est
une force conservative. L'énergie mécanique d'un système en chute libre
est constante.
1.2. Les
caractéristiques de la trajectoire parabolique suivie par l’avion
sont-elles compatibles avec une chute libre de l’avion ? Argumenter
votre réponse avec un calcul d’énergie.
On prend l'altitude de départ et de fin de la parabole comme origine des altitudes, donc de l'énergie potentielle de pesanteur.
Energie mécanique au début de la parabole : ½mv2 avec v =527 / 3,6 =146,4 m /s.
Energie mécanique au sommet de la parabole :
½mvs2 +mgh avec vs = 355 / 3,6 = 98,6 m/s et h = 8200-7600 = 600 m.
Dans l'hypothèse d'une conservation de l'énergie mécanique : ( g étant supposé constant égal à 9,8 m/s2)
v2 = vs2 +2gh ; 146,42 = 98,62 + 2*9,8 *600 ;
2,14 104 = 2,14 104. L'hypothèse est validée.
2. Intensité du champ de pesanteur dans un vol Zéro-G.
2.1. En détaillant votre raisonnement, montrer que l’intensité de la pesanteur gh, en un point situé à l’altitude h au-dessus de la surface de la Terre, peut s’écrire :
gh =G M /(R+h)2.
Poids de l'avion : P = mgh ;
Force de gravitation exercée par la terre sur l'avion : F = GMm /(R+h)2.
P = F ; mgh = GMm /(R+h)2.
Simplifier par m : gh =G M /(R+h)2.
2.2.
Justifier, à partir du résultat précédent, qu’il est légitime de
considérer que l’intensité de la pesanteur est constante lors d’un vol
Zéro-G.
Au sol g0 = GM / R2 ; gh =g0[R /(R+h)]2 = g0[1 /(1+h / R)]2 ;
[1 /(1+h / R)]2 = 1 /(1 +8200 / (6,38 106)]2 =0,997.
gh =0,997g0.
|
|
|
3. Durée des phases d’apesanteur.
On étudie le mouvement dans le repère xOy donné ci-dessous, le point O
étant le début de la parabole. On considère que l’intensité de la
pesanteur terrestre est constante lors d’un vol Zéro-G et qu’elle est
égale à g = 9,8 N.kg-1.

3.1. Énoncer la deuxième loi de Newton.
Dans
un
référentiel galiléen, la somme vectorielle des forces extérieures
appliquées à un solide est égale à la dérivée par rapport au temps du
vecteur quantité de mouvement et si la masse est constante au produit
de la masse M du solide par
l'accélération de son centre d'inertie.
3.2. Montrer que les équations horaires x(t) et y(t) d’un système en chute libre ont pour expressions :
x(t) =v0 cos(a ) t ; y(t) =-½g t2 +v0 sin(a ) t.
ax = 0 ; ay = -g.
La vitesse est une primitive de l'accélération :
vx(t) = A ; vy(t) = -gt +B avec A et B des constantes déterminées par les conditions initiales.
vx(t) = v0 cos a ; vy(t) = -gt + v0 sin a .
La position est une primitive de la vitesse :
x(t) = v0 cos a t + C ; y(t)= -½gt2 + v0 sin a t +D, avec C et D des constantes déterminées par les conditions initiales x(t=0)=0 et y(t=0) = 0.
x(t) = v0 cos a t ; y(t)= -½gt2 + v0 sin a t .
|
|
|
|
3.3.
En exploitant les équations horaires, calculer la durée d’apesanteur.
Ce résultat est-il cohérent avec la donnée du document 2 ?
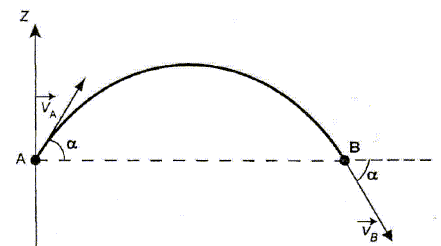
A la date tB, le système se trouve au
point B, de même altidude que le point A, avec une vitesse vB
= vA = 146 m/s.
vy A = -gtA + v0 sin a ; vy B = -gtB + v0 sin a ; vx A =vx B =v0 cos a ;
Par suite vy A = -vy B ; tB -tA = 2v0 sin a / g = 2*146 sin 47 / 9,8 ~22 s.
La valeur trouvée est cohérente avec le texte.
3.4. Quels paramètres faut-il modifier pour augmenter la durée d’apesanteur ?
tB -tA = 2v0 sin a / g
On peut augmenter la vitesse au début de la parabole ainsi que la valeur de l'angle a.
Cela est techniquement difficile à réaliser.
|
|