Des aurores polaires et des électrons. Bac S Centre étranger 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Dans le cas d'une particule dite relativiste, la question se pose de savoir comment sont modifiées les expressions des quantités déja définies dans le cadre de la mécanique classique : quantité de mouvement, énergie cinétique... 1. Effets relativistes. 1.1. Dilatation du temps. 1.1.1. Lorsque les effets de la relativité restreinte se font sentir, on parle de "dilatation des durées". Montrer en quoi cette expression est appropriée. La durée d'un phénomène est une notion relative. Deux observateurs en mouvement rectiligne uniforme relatif ne donnent pas la même durée à un phénomène physique. La durée propre, la plus courte, ( intervalle de temps entre deux événements se produisant au même lieu de l'espace ) est lue sur l'horloge du référentiel observateur immobile par rapport au phénomène. On parle de ralentissement des horloges mobiles ou de dilatation des durées. Dt = g Dt0 avec g =[1-(v/c)2]-½ ; Dt durée mesurée et Dt0 temps propre. Si v << c, alors Dt ~ Dt0 ( pas de dilatation des durées). Si v / c = 0,85, alors Dt ~ 2 Dt0 . 1.1.2. On considère une particule dont la vitesse dans un référentiel terrestre est égale à 10% de celle de la lumière. On mesure Dt = 1,0 ns. Estimer Dt0 et commenter. g = [1-(v/c)2]-½  = [1-(0,1)2]-½ =1,0050. Dt0  =Dt / g =1,0 /1,005 ~0,99 ns. Cette particule n'est pas relativiste, les effets de la relativité restreinte sont négligeables. 1.1.3. L'extrait du livre d'Etielle Klein se termine par ce passage : " Les constantes fondamentales de la physique y sont modifiées de sorte que les phénomènes physiques habituellement cahés dans la vie courante deviennent manifestes ". Que veut dire l'auteur ? Illustrer cela en envisageant que la constante c ait une valeur plus petite. Le rapport (v/c)2 se rapproche assez rapidement de 1 si c est plus petit. En conséquence g devient grand et le phénomène de dilatation des durées est davantage perçu. 1.2. Energie cinétique et vitesse des électrons. Les graphes (a) et (b) représentent l'évolution du rapport (v/c)2 en fonction de l'énegie cinétique d'un électron dans le cas de la théorie classique et dans le cas de la théorie relativiste. Les échelles utilisées pour le graphe (b) permettent un aggrandissement du graphe (a) au voisinage de l'origine. 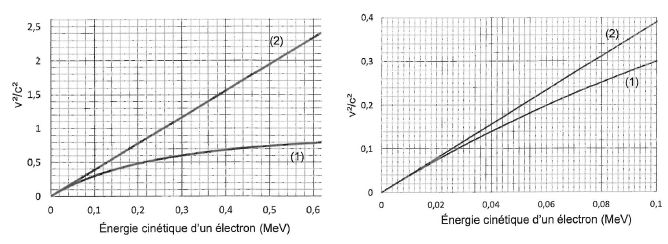1.2.1. Des deux représentations (1) et (2), identifier celle qui correspond à la théorie classique. Justifier en donnant deux arguments. (2) Théorie classique ; (1) théorie relativiste. Courbe (2) : droite passant par l'origine. L'énergie cinétique est proportionnelle à (v/c)2 ; or c est constante, donc l'énergie cinétique est proportionnelle à v2. Courbe (2) : (v/c)2 peut être supérieure à1, ce qui est contraire à la théorie relativiste. Courbe (1) : (v/c)2 ne peut pas être supérieure à1, ce qui est en accord avec la théorie relativiste. 1.2.2 Montrer qu'à partir d'une valeur de la vitesse égale à 1,2 108 m/s, les électrons peuvent être considérés comme relativistes. On considèrera que les effets relativistes sont négligeables si l'écart relatif entre les valeurs de l'énergie cinétique selon les lodèles classique et relativiste est inférieur à 10 %. (v/c)2 = (1,2 / 3)2 = 0,16. 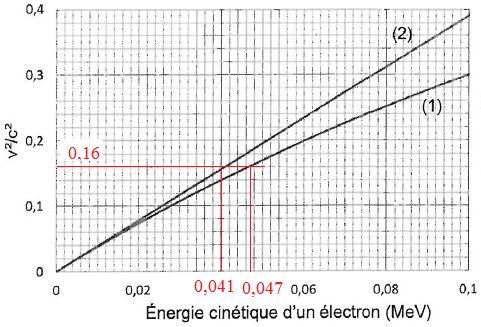(0,047-0,041) /0,041 ~0,15 ( 15 %). 2.. Des aurores polaires. Des particules chargées en provenance du Soleil mais aussi d'autres étoiles balaient le système solaire. Ce sont des vents stellaires dans lesquels on trouve notamment des électrons. Ces derniers peuvent pénétrer dans l'atmosphère terrestre et entrer en collision avec les atomes d'oxygène ou d'azote, leur transférant partiellement leur énergie. Cette énergie est ensuite rayonnée sous forme lumineuse lorsque ces atomes se désexcitent provoquant parfois de magnifiques spectacles d'illumination du ciel, visibles de la surface de la terre, généralement dans les régions polaires : les aurores boréales. 2.1. Donner un ordre de grandeur de la valeur de la longueur d'onde d'une onde électromagnétique dans le domaine du visible. Les longueurs d'onde du domaine visible sont comprises entre 0,4 µm et 0,8 µm, soit de l'ordre de 6 10-7 m. ( ordre de grandeur 10-6 m). 2.2. Montrer par un calcul, qu'il n'est pas nécessaire que les électrons pénétrant dans l'atmosphère soient relativistes ( au sens de la question 1.2.2 ) pour participer à la création des aurores boréales. Energie moyenne correspondant à un photon du domaine visible : E = h c / l = 6,63 10-34 *3,0 108 / (6 10-7)=3,3 10-19 J. Energie cinétique d'un électron non relativiste : Ec = ½mv2 avec v ~ 1,2 108 m/s. Ec = 0,5 *9,1 10-31 *(1,2 108)2 ~6,6 10-15 J. Ces électrons sont suffisamment énergétiques pour exciter les atome de''oxygène ou d'azote de l'atmosphère. .

menu