Ondes et
électrons. Bac S Centre étranger 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
En 1912,
Max Von Laue soumet un cristal à des ondes électromagnétiques de courte
longueur d'onde, les rayons X. Il découvre ainsi sa structure. Les
solides cristallins présentent au niveau atomique un arrangement
parfaitement ordonné et régulier dans les trois directions de l'espace.
Cet arrangement est caractérisé par la distance a entre deux entités (
atome, ion ou molécule ). Cette distance est de l'ordre de 0,1 nm. Les
solides cristallins ont la propriété de diffracteriune onde de longueur
d'onde dont la valeur est voisine de la distance a.
1. Diffraction d'un
faisceau d'électrons.
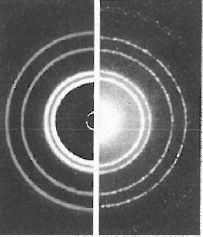
Les deux représentations ci-dessous montrent la figure de diffraction
d'un faisceau de rayons X ( à gauche ) et d'un faisceau d'électrons ( à
froite ) après passage au travers d'une fine feuille faite de petits
cristaux d'aluminium.
Source : A P French and Edvin F. Taylor, introduction to quantum
physics , New York. W.W.Norton 1978.
1.1. Quelle
condition sur la longueur d'onde permet d'observer le phénomène de
diffraction ?
La longueur d'onde doit être du même ordre
de grandeur que la dimension de l'obstacle ou de la distance entre deux
entités ( atome, ion ).
1.2. Expliquer en quoi la figure
ci-dessus illustre l'hypothèse d'un comportement ondulatoire des
électrons.
La diffraction est un phénomène caractéristique d'une onde. Le faisceau
d'électrons étant diffracté par passage au travers d'une fine
feuille d'aluminium, la figure de droite met en évidence le caractère
ondulatoire de ce faisceau d'électrons.
1.3. Donner la
relation de De Broglie qui prend en compte ce comportement ondulatoire
des électrons. Quelle est sa signification ?
La longueur d'onde l et la quantité de mouvement p d'une particule sont
reliées par : l =
h / p.
Un corpuscule matériel peut avoir un caractère ondulatoire.
|
|
|
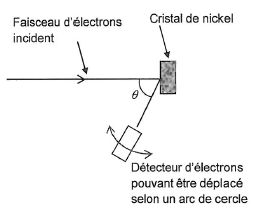
En
1927, lLes américains C J Davisson et L Germer apportent la première
preuve expérimentale du comportement ondulatoire de particules de
masse non nulle. Ils observent ainsi la diffraction d'un faisceau
d'électrons de vitesses identiques, par un cristal de nickel. Le schéma
de principe du montage expérimental est représenté ci-dessous.
2. Obtention du faisceau
d'électrons.
Des électrons émis sans vitesse initiale par un filament sont accélérés
par le champ électrostatique horizontal supposé uniforme qui règne
entre deux plaques planes verticales A et B aux bornes desquelles on
applique une tension électrique de l'ordre de 100 V.Données :
masse de l'électron m = 9,11 10-31 kg ; e = 1,60 10-19
C ; h = 6,63 10-34 J s ;
la distance entre les plaques est inférieure à 1 m.
2.1 Montrer que le
poids de l'électron est négligeable devant la force électrostatique
qu'il subit.
P = mg ~9,1 10-31*10 ~9,1 10-30 N.
Champ électrostatique E = U /AB = 100 / 0,9 = 1,1 102 V m-1
si AB = 90 cm.
Valeur de la force électrostatique F = eE = 1,6 10-19 *1,1 102
~2 10-17 N, très supérieure au poids.
2.2. Représenter
sur un schéma la force électrostatique F subie par l'électron entre les
plaques et le champ E. Justifier.
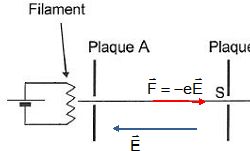
Pour accélérer au mieux les électrons entre A et B, le travail de la
force F doit être moteur. Les vecteurs F et AB doivent être colinéaires
et de même sens. Par contre, la charge de l'électron étant
négative, la force F et le champ sont colinéaires et de sens contraire.
|
|
|
|
2.3. Montrer qu'en sortie du
dispositif, l'expression de la vitesse v d'un électron est v = [2eU / m]½.
Méthode 1. On choisit un axe horizontal orienté à droite, origine : plaque A.
Accélération des électrons : a = eE / m.
Vitesse v(t) = eE/ m t. ( la vitesse initiale est nulle ).
Position : x = ½eE / m t2.
B est atteinte à la date t = [2AB m /(eE)]½ = [2AB m /(eE)]½ ;
vitesse en B : eE / m [2AB m /(eE)]½ = [2AB eE/m]½ =[2eU / m]½.
Autre méthode :
Travail de la force électrostatique entre A et B : W = eU.
Théorème de l'énergie cinétique entre A et B : ½mv2-0 = eU.
Par suite v = [2eU / m]½.
2.4. Pour observer
la diffraction d'un faisceau d'électrons par le nickel, la longueur
d'onde de matière associée doit être de l'ordre de 0,1 nm.
2.4.1. Montrer que
dans ce cas l'expression de la tension U est donnée par : U = h2
/ (2mel2).
l = h
/ (mv) ; l2
= h2 / (mv)2 ; v2 = 2eU / m ;
l2
= h2 / (2eUm) ; U = h2 / (2mel2).
2.4.2. Retrouver
l'ordre de grandeur de la tension U que Davisson et Germer ont dû
choisir pour leur expérience.
U = (6,63 10-34)2 / [2*9,11 10-31*1,6
10-19 *10-20]=1,5 102 V.
3. Une application
technologique du phénomène : le microscope électronique.
Deux chercheurs allemends ont conçu en 1931 un prototype de microscope
électronique utilisant un faisceau d'électrons accélérés par une
tension U de l'ordre de 100 kV. Sachant que la résolution ( plus petite
distance séparant deux objets que l'on peut distinguer ) d'un
microscope optique ou électronique est proportionnelle à la longuer
d'onde du rayonnement utilisé, expliquer en quelques lignes une raison
qui a pu motiver les chercheurs à se lancer dans l'élaboration d'un
microscope électronique.
Le microscope optique utilise la lumière visible dont la longueur
d'onde moyenne est de l'ordre de 0,6 µm.
Deux petits objets distants de 0,6 µm provoquent la diffraction de la
lumière. Ces objets ne peuvent pas être distingués.
Le microscope électronique utilise un faisceau d'électrons dont la
longueur d'onde est de l'ordre de 0,1 nm.
Deux petits objets distants de 0,1 nm provoquent la diffraction du
faisceau d'électrons. Ces objets ne peuvent pas être distingués.
6 10-7 / (0,1 10-9) ~6 103.
Le microscope électronique permet d'observer des détails 6000 fois plus
petits que le microscope optique.
|
|