La gravitation : exoplanète, satellites. Travail, énergie. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exoplanète. Qu'est-ce qu'une exoplanète ou planète extrasolaire ? C'est une planète en orbite autour d'une étoile autre que le soleil. Que renferme l'espace entre la terre et Gliese 581 ? La quantité de matière est si faible (fragments d'astéroïdes par exemple ) entre le système solaire et Gliese 581 que l'on peut dire que l'espace est constitué de vide. Définir une année de lumière ; calculer sa valeur. Donner un ordre de grandeur de cette valeur. C'est la distance parcourue dans le vide par la lumière pendant une année. d = c t = 3,0 108 *365*24*3600 = 9,46 1015 ~9,5 1015 m. Ordre de grandeur 1015 m. Calculer la distance séparant la terre de Gliese 581 distante de 20 années de lumière de la terre. 20 *9,46 1015 ~1,89 1017 m ~ 1,9 1014 km. Pourrait t-on observer ce qui se passe à l'heure actuelle sur Gliese 581 à l'aide d'un télescope très performant ? Pour voir un objet, la lumière qu'il émet doit parenir à nos yeux. La distance parcourue par la lumière entre le télescope et Gliese 2B étant très grande, la lumière arrivera avec un retard. Nous voyons l'objet dans le passé. Voir loin, c'est voir dans le passé. Calculer le poids d'un objet de masse 1,0 kg à la surface de Gliese 581 sachant que le rayon de cette planète est 2 fois plus grand que le rayon terrestre terre et que cette exoplanète est 5 fois plus massive que la terre. D'après la loi de gravitation universelle, le poids d'un objet est proportionel à la masse de la planète et inversement proportionnel au carré de son rayon. Sur terre le poids d'une masse de 1,0 kg est égal à 10 N. P = 10 *5 / 22 = 12,5 ~ 13 N. Exercice 2 : satellite Hélios 2B. Hélios 2 B est sur une orbite héliosynchrone. Il survole toujours à la même heure solaire locale une région donnée de la terre. Quel est le référentiel le plus adapté pour l'étude du mouvement d'un satellite terrestre ? Le référentiel géocentrique est le plus adapté pour cette étude. Quel est l'intérêt d'une orbite héliosynchrone ? Toute la surface de la tere est couverte et les appareils de détection donnent des mesures précises. La trajectoire d'hélios 2B est circulaire. Pour quelle raison ce satellite est-il soumis au moins à une force ? D'après le principe d'inertie, le centre de gravité d'un système soumis à aucune force ( ou à des forces qui se compensent ) est soit animé d'un mouvement rectiligne uniforme, soit immobile, dans un référentiel galiléen. Hélios 2B étant animé d'un mouvement circulaire, il est soumis à des forces qui ne se compensent pas. Il est soumis à la seule attraction terrestre. Exprimer puis calculer la force de gravitation exercée par la terre sur ce satellite. Masse du satellite m = 4,2 tonnes ; altitude h = 675 km. Masse de la terre M = 6,0 1024 kg ; rayon terrestre R = 6400 km. F = G M m /(R+h)2 = 6,67 10-11 *6,0 1024 * 4,2 103 /(6,4 106 +6,75 105)2 =3,37 104 ~3,4 104 N. Quel est l'ordre de grandeur de cette valeur, 104 N. Schématiser la situation. . . 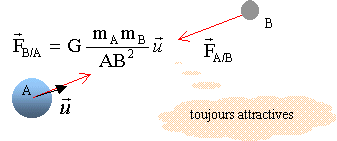Exercice 3 : satellite Télécom II. Ce satellite de télécommunication est placé  à 36000 km d'altitude au dessus du golfe de Guinée. Il survole en permanence la même région du globe.Sa trajectoire est circulaire et sa vitesse vaut v = 11 000 km / h. Quelle est la trajectoire de ce satellite dans un référentiel teerrestre ? Un satellite géostationnaire paraît immobile pour un observateur terrestre. Quel est l'intérêt d'une orbite géostationnaire ? Le satellite couvre une importante région terrestre. Les antennes terrestres, pointant vers un tel satellite, sont fixes. Exprimer puis calculer la force de gravitation exercée par la terre sur ce satellite. Masse du satellite m = 1,0 tonne. F = G M m /(R+h)2 = 6,67 10-11 *6,0 1024 * 1,0 103 /(6,4 106 +3,6 107)2 =2,23 102 ~2,2 102 N. Comparer cette force à celle exercée par la terre sur Hélios 2B. FHélios / Ftélécom II =3,37 104  / (2,23 102) ~1,5 102. d'après les données, vérifier que télécom II est bien géostationnaire. Dans le référenteil géocentrique, ce satellite décrit une circonférence 2 p(R+h) en une journée( durée T = 24 *3600 s) à la vitesse v. 2 p(R+h) = v T ; v = 6,28 (6,4 106 +3,6 107) /(24*3600)=3,08 103 m/s = 3,08 km/s 3,08  *3600 = 1,1 104 km/ h, en accord avec les données. Pendant la chute. Partie A : Des conditions extrêmes. Lors de cette aventure, F. Baumgartner est équipé d’un scaphandre lui permettant de résister à des conditions très particulières. Le scaphandre est pressurisé. La pression de l’air dans le scaphandre patm est égale à 101,3 x 103 SI, valeur de la pression atmosphérique au sol le jour du saut. La visière du casque de F. Baumgartner a une surface d’aire S égale à 500 cm². On note F la valeur de la force pressante exercée par l’air placé dans le scaphandre sur la visière. On rappelle la relation p = F / S qui relie la pression p à la force pressante F exercée sur une surface S. Rappeler l’unité SI de pression. Pascal ( Pa). Montrer que la valeur de la force pressante F exercée par l’air contenu dans le scaphandre sur la visière a pour valeur 5 065 N. F =p S = 101,3 103 *500 10-4 =5065 N. A l’altitude de 38 970 m, l’atmosphère est extrêmement raréfiée et la pression extérieure peut être considérée comme nulle. Prévoir si la visière est éjectée ou plaquée contre le visage de F. Baumgartner, dans l’hypothèse où elle est mal fixée. Justifier la réponse. La force pressante exercée par l'air intérieur du scaphandre est dirigée vers l'extérieur. La visière peut être éjectée. Le scaphandre doit également protéger Baumgartner du rayonnement solaire, en particulier du rayonnement ultra-violet. Citer deux effets nocifs du rayonnement ultra-violet sur le corps humain. Les UV provoquent  des lésions dégénératives dans les cellules cutanées et une réaction inflammatoire de l'oeil. Partie B : Franchir le mur du son. Félix Baumgartner chute sans vitesse initiale depuis un point noté A, situé à 38 970 m d’altitude. Sa masse m, scaphandre et parachute compris, est égale à 120 kg. On considère que la seule force qu’il subit est son poids P force verticale dirigée vers le bas. On veut connaître la vitesse atteinte au point B situé à la verticale du point A, à une distance h égale à 6 955 m. On rappelle que P = m  g (on considère que g reste constant au cours de la chute.) Montrer que le poids P de Félix Baumgartner (équipement compris) vaut 1,2 x 103 N. Donnée : valeur approchée de l’intensité de pesanteur g = 10 N kg-1. P = mg = 120 *10 = 1,20 103 N.  Choisir parmi les propositions ci-dessous l’expression du travail du poids pendant cette chute. a) m g / h  ; b) m g h ;  c) – m g h. Le travail du poids est moteur en descente et vaut m g AB = m g h. Vérifier que le travail du poids durant cette chute vaut 8,3 x 106 J. WAB(P) =m g h = 120*10 *6955 =8,3 06 J. En appliquant le théorème de l’énergie cinétique à Félix Baumgartner lors de son passage du point A au point B, on a obtenu la relation suivante décrivant l’énergie cinétique du parachutiste en B, EC(B)  = WAB(P) Rappeler la relation entre l’énergie cinétique EC(B) au point B et la vitesse atteinte au point B, VB. EC(B) = ½mV2B. Calculer alors la vitesse VB en m s-1 puis en km h-1. Préciser si la valeur trouvée est en accord avec celle donnée dans le texte d’introduction ( 1342,8 km/ h ). ½mV2B = m g h ; V2B =2 g h ; VB = (2 g h)½ =(2*10*6955)½ =373 m /s ou 373*3,6 =1,34 103 km/h, en accord avec le texte. .

menu