Mathématiques.
Concours Aspts Sud Est 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
1.
Un pâtissier souhaite réaliser des tartelettes fraise / framboises. Il
dispose de 411 framboises et 685 fraises. Calculer le nombre maximum de
tartelettes identiques qu'il peut confectionner.
411 = 3 x 137 ; 685 = 5 x 137.
PGCD(411 ; 685) = 137.
Combien y aura-t-il de fraises et de framboises sur chaque tartelette ?
5 fraises et 3 framboises.
2.
Trois enfants se partagent une tablette de chocolat. Le premier prend
le tiers de la tablette et le second le quart. Le troisième prend les
deux cinquièmes du reste. Quel calcul permet de trouver la part du
troisième ?
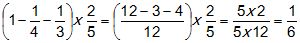
3. ABC est un triangle rectangle en A. AB = 3 cm ; AC = 4 cm. Calculer la longueur exacte du côté BC en justifiant.
Phytagore : BC2 = AB2 + AC2 = 9+16 = 25 ; BC = 5 cm.
Exprimer la tangente de l'angle B par rapport aux côtés du triangle.
tan B = côté opposé / côté adjacent = AC / AB = 4/3 = 1,33.
Exprimer le sinus de l'angle C par rapport aux côtés du triangle.
sinus C = côté opposé / hypothènuse = AB / BC = 3 / 5 = 0,60
4.
ABC est un triangle tel que AB = 2,5 cm ; AC = 3 cm et BC = 4 cm. On
place le point E de la droite (AB) mais n'appartenant pas au segment
[AB] tel que AE = 1,5 cm et le point F de la droite (AC) mais
n'appartenant pas au segment [AC] tel que AF = 1,8 cm.
Représenter la figure, sans tenir compte des dimensions exactes.
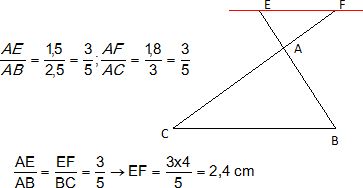
Que peut-on dire des droites (BC) et (EF) ? Calculer EF.
Ces droites sont parallèles.
5. Un rectangle a pour dimensions L =racine carrée (245) cm et l=racine carrée (80) cm.
Calculer son périmètre.
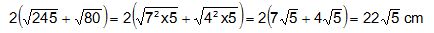
Calculer l'aire du rectangle.
7 racine carrée (5) fois 4 racine carrée (5) = 7 x4x5 =140 cm2.
|
| .
. |
|
|
6. Soit la série : 7 ; 18 ; 8 ; 16 ; 12 ; 5 ; 16 ; 15 ; 19.
Quelle est la médiane de cette série ? Justifier.
Ordonner : 5 ; 7 ; 8 ; 12 ; 15 ; 16 ;16 ; 18 ; 19.
La médiane est égale à 15. Elle partage la série en deux groupes de même effectif.
Quelle est l'éttendue de cette série ? Justifier.
La plus petite note est 5 et la plus grande est 19 : étendue 19-5 = 14.
Quel est le premier quartile ? Justifier.
Au moins 25 % des valeurs de la série sont inférieures ou égales au premier quartile.
N/4 = 9/4 = 2,25.
Le premier groupe doit contenir les trois premières valeurs. 8 est le premier quartile.
Quel est le troisième quartile ? Justifier.
Au moins 75 % des valeurs de la série sont inférieures ou égales au troisième quartile.
Ce groupe doit contenir les trois dernières valeurs. 16 est le troisième quartile.
7. Calculer le volume d'un cylindre dont la base a un diamètre D= 60 cm et dont la hauteur est h= 3 m. V = pR2h avec R = 0,30 cm.
V = 3,14 *0,302 *3 =0,848 m3.
Combien de litres d'eau ce cylindre peut-il contenir ?
848 litres.
8. Donner les écritures scientifiques de :
6 x 108 x 3 x10-4 = 18 104 = 1,8 105.
3 x10-3 x 4 (102)2 / (20 10-4)=0,6 105 = 6 104.
28400000 = 2,84 107.
0,00049 = 4,9 10-4.
|
|
|
|
9. Calculer :
108032-98032 = (10803+9803)(10803-9803)=2,0606 107.
10. Soit la fonction affine f telle que f(3)=2 et f(-1) =-10.
Déterminer le système d'équations qui permettra de déterminer f puis le résoudre.
f est de la forme f(x)=ax+b.
2 = 3a+b et -10 = -a+b.
Soustraire : 2+10 = 3a+a ; a = 3 ; par suite b = -7.
11. Factorisez l'expression B=(16-x)2-25.
Différence de deux carrés : (16-x+5)(16-x-5)=(21-x)(11-x).
Développer et réduire B.
B = 256 +x2-32x-25 = x2-32x+231.
Calculer B pour x = 4.
B = 122-25 = 144-25 =119
12. Une urne contient des boules jaunes, des boules bleues et des boules rouges.
La probabilité de tirer une boule jaune est p(J) = 0,2.
La probabilité de tirer une boule bleue est la même que celle de tirer une boule rouge.
Quelle est la probabilité de tirer une boule rouge ?
1 = p(J) + p(B) + p(R) ; p(B) + p(R) =1-0,2 = 0,8.
p(B) = p(R) =0,4.
|
|
|
|