Mathématiques.
Concours Aspts Ouest 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une
seule bonne réponse par question.
1. Quel est le résultat de l'opération : (4-6) x (5+(3-(-2)) x 2 ) ?
(-2) x(5+5 x 2) =(-2) x 15 = -30.
-30 (vrai) ; -2 ; -40 ; 30.
2.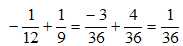
3. Pendant les soldes, un
commerçant diminue le prix d'un article de 60 %. Il coûte désormais 80
€. Cet article valait avant le rabais : 120 € ; 140 ; 200 €
(vrai) ; 320 €.
80 / (1-0,60) = 200 €.
4.
Les dernières notes de Jean en dictée sont les suivantes : 14 ; 17 ; 0
; 5. Quelle note doit-il obtenir àla prochaine dictée s'il veut
unemoyenne de 10 ? 10 ; 14 (vrai) ; 16 ; 18.
(14+17+0+5+x) / 5 = 10 ; x = 14.
5.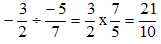
6.
f désigne une fonction affine définie par f(x) =-1,5x+1. L'antécédent
de 0 par f est : (2/3 vrai ; 1 ; -1,5 ; 0,5 ). 0 = -1,5 x+1 ; x =
1 / 1,5 = 2 / 3.
7. 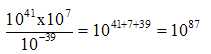 . .
8. On pose f(x)= -x2+4x+1. L'image de -2 par est : -3 ; 1 ; 13 ; -11(vrai).
f(-2) =-(-2)2+4(-2)+1 = -4-8+1= -11.
9. Quelle est l'écriture scientifique de 159 10-5 ?
1,59 * 102 * 10-5 = 1,59 10-3.
10. ABC est un triangle rectangle en B. AB = 4,8 cm ; AC = 8 cm. Calculer BC.
AB2+BC2=AC2 ; BC2=AC2 -AB2 =64-4,82 = 40,96 ; BC = 6,4 cm.
11. Trouver la formule dévelopée de :
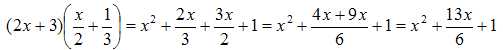
|
| .
. |
|
|
12. EGF est un triangle rectangle en F. EF = 6 cm. L'angle issu de E mesure 27°. Quelle est la mesure de EG ?
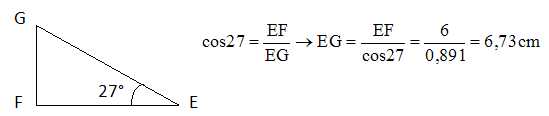
13. On lance deux fois une pièce de monnaie. Qu'elle est la probabilité de n'obtenir aucun pile ?
0 ; 1/3 ; 1/4 (vrai) ; 3/4.
Probabilité d'avoir face au premier lancer : 0,5 ; probabilité d'avoir face au second lancer : 0,5.
0,5*0,5 = 0,25.
14.
Les solutions de l'équation 2x(3+4x)=0 sont :
x=0 et 3+4x=0 soit x = -3/4.
15. Pour une douche on consomme
80 litres d'eau de moins que pour un bain. Jean a pris une douche ;
Marie a pris un bain et ils ont consommés à eux deux 230 litres d'eau.
Quelle est la quantité d'eau utilisée par Marie ? 75 L ; 80 L ; 150 L ;
155 L (vrai).
x : volume d'eau d'un bain ; x-80 : volume d'eau d'une douche.
x +x-80 = 230 ; 2x = 310 ; x = 155 L.
16. L'aire d'un triangle est 25 cm2. On réaise un aggandissement de ce triangle et on double la longueur des côtés. L'aire est alors de 50 cm2 ; 75 cm2 ; 100 cm2 (vrai) ; 125 cm2.
17. Quelle est la forme factorisée de 25-(2x+3)2 ?
Différence de deux carrés (5+2x+3)(5-2x-3)=(2x+8)(2-2x).
18. 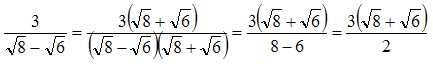
19. 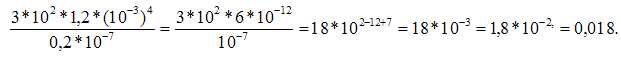
|
|
|
|
20.
ABC est un triangle quelconque de sommet A, M appartient à [AB] et N
appartient à [AC]. Les droites (BC) et (MN) sont parallèles. AN=5 ;
MN=3 ; AB=9,3 ; AC=8. Quelle est la mesure de BC ?
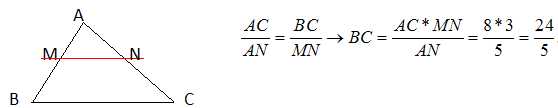
21. ABC est un triangle rectangle en A. BC = 5,1 cm et l'angle issu de B mesure 31°. Le côté AC est donné par :
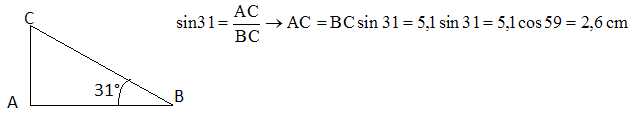
22. 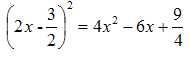
23.
La série suivante : 13 ; 21 ; 19 ; 18 ; 27 ; 15 ; 22 ; 23 a pour médiane. 19 ; 21 ; 40 ; 20 (vrai).
Ordonner : 13 ; 15 ; 18 ; 19 ; 21 ; 22 ; 23 ; 27.
20 partage la série en deux groupes ayant le même effectif.
24.
Le prix du baril de pétrole a baissé de 40 % puis de 30 %. Il a donc baissé au total de : 50 % ; 58 % (vrai) ; 70 % ; 74 %.
Prix apère la première baisse : 0,60 ; prix après la seconde baisse : 0,60*(1-0,30 ) =0,42.
la baisse est donc de 1-0,42 = 0,58 (58 %).
25. Le PGCD de 468 et de 702 est : 234 (vrai) ; 117 ; 18 ; 13.
468 = 22 x 32 x 13 ; 702 = 2 x 33 x13 ; PGCD(468 ; 702) =2 x 32 x 13 =234.
26. Quelles sont les solutions du système 2x+6y=5 et 3x-4y =1 ?
6x+18y =15 et 6x-8y = 2.
Soustraire : 18y+8y =15-2 ; 26 y = 13 ; y = 0,5 par suite x = 1.
27.
Un maraîcher a vendu un quart de sa production de tulipes à des
fleuristes et 3 / 10 de sa production à des jardineries. Il lui reste
540 000 fleurs pour les marchands ambulants. Combien avait-il de fleurs
initialement ?
On note x le nombre de fleurs : 0,25 x +0,3 x + 540 000 = x ; 0,45 x = 540 000 ; x = 1 200 000.
28. L'inverse de -7 / 4 est : -4 / 7.
29.
Les solutions de l'équation (2x+1)-(x-3)=0 sont :
2x+1-x+3=0 ; x =4=0 ; x = -4.
30. Le nombre de téléphones
portables dans le monde est passé de 4 à 5 milliards entre 2009 et
2011. L'augmentation en pourcentage est :
10 % ; 20 % ; 25 % (vrai) ; 50 %.
(5-4) / 4 = 0,25 ( 25 %).
31.
Une vitesse de 28 m/s représente en km / h : 100,8 (vrai) ; 10,8 ; 1,8 ; 0,18.
28*3,6 = 100,8 km/h.
32. Dans une ferme il y a des vaches et des poules. On compte 36 têtes et 100 pattes. Combien y -a-t-il de vaches ?
25 ; 20 ; 14 (vrai); 12.
On note x le nombre de poules et y le nombre de vaches.
x+y = 36 et 2x +4y = 100.
2x +2y = 72 et 2x +4y = 100.
Soustraire :2y = 28 ; y = 14.
33. 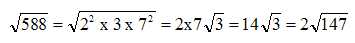
34. x désigne un angle aigu d'un triangle rectangle. On sait que cos x = 0,6. Donner la valeur de sin x.
0,6 ; 0,8 (vrai) ; -0,8 ; 1.
sin2 x + cos2 x = 1 ; sin2 x = 1-0,62 = 0,64 ; sin x = 0,8.
35.
Au parc d'attraction, on propose deux tarifs d'entrées. Le tarif A :
l'entrée est de 19 €. Le tarif B avec abonnement pour l'année : on paie
un abonnement de 75 €, l'entrée est alors de 6 €. x représente le
nombre d'entrées. A partir de combien d'entrées, le tarif B, est-il le
plus intéressant ?
A : on paie 19 x ; B on paie : 75 + 6x.
75 +6x <19x ; 75 < 13 x ; x > 75/13 ( environ 6 entrées ). Le tarif B est le plus intéressant à partir de 6 entrées.
36. EDF est un triangle quelconque et C désigne son cercle circonscrit ; C a pour centre le point O. Alors :
O est le point d'intersection des médianes ( faux).
O est le point d'intersection des bissectrices ( faux). (Point de concours des médiatrices ).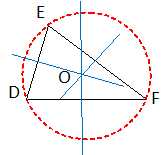
L'angle
du triangle EDF, issu de D, a pour mesure la moitié de l'angle EOF. (
vrai) ( angle inscrit et angle au centre interceptant le même
arc).
L'angle du triangle EDF, issu de D, a pour mesure ledouble de l'angle EOF. ( faux)
37. Sur un cercle C, on place quatre points A, B, C et M. L'angle BAD mesure 47°. Quelle est la mesure de l'angle BMD ?
23,5° ; 47°(vrai) ; 94° ; on ne peut pas savoir.
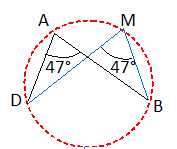
Angles inscrits interceptant le même arc.
38. Quelle est l'ensemble solution de l'inéquation :
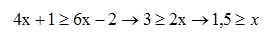
39. Un globe terrestre a la forme d'une sphère de diamètre D = 60 cm. Calculer la valeur exacte de son aire en cm2.
4pR2 avec R = 30 cm. 4x302 p = 3600 p.
40. Le nombre p vaut 3,1415926... Quelle est sa valeur approchée à 10-3 près ?
3,142.
|
|
|
|