Le saut de Félix Baumgartner. Concours orthoptie Nantes 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . L'aventurier autrichien Felix Baumgartner est devenu dimanche 14 octobre 2012 le premier homme à franchir le mur du son en chute libre après s'être lancé d'une capsule accrochée à un ballon d'hélium d'une altitude reccord d'un peu plus de 39,0 km dans le ciel du Nouveau-Mexique. On peut décomposer ce saut en trois phases : 1ère phase : elle commence lorsque le parachutiste se laisse tomber sans vitesse initiale de sa capsule et se termine lorsqu'il atteint la vitesse maximale vmax = 1,3419 103 km/h, soit 1,24 fois la vitesse du son. Les frottements et la poussée d'Archimède sont négligés durant cette phase.  Il est tombé en chute libre durant 4 min 20 s avant ouverture de son parachute. 2ème phase : elle débute lorsque la vitesse maximale est atteinte. Il existe alors une force de frottement de type f = kv due à l'air. On négligera la poussée de l'air sur le parachutiste. 3ème phase : elle débute lorsque le parachutiste ouvre son parachute. Elle ne sera pas étudiée ici. Etude du saut dans le cadre d'une chute libre.  Rappeler l'expression vectorielle de la force gravitationnelle exercée par la terre sur un corps de masse m séparés d'une distance D. 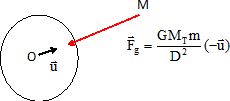Rappeler l'expression vectorielle du poids dans ces conditions. 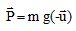En déduire l'expression de la constante de pesanteur g en fonction de MT, G et D. Calculer g. g = GMT /D2. On donne RT =6,371 103 km , h = 39,0 km, G =6,67 10-11 SI, MT = 5,97 1024 kg. Le parachutiste est à la hauteur h de la terre. g = GMT /(RT+h)2 = 6,67 10-11 *5,97 1024 / (6,371 106+ 39,0 103)2 =9,69 m s-2. On prendra par la suite g = 9,75 m s-2. le mouvement est étudié dans un référentiel terrestre supposé galiléen sur un axe Oz dirigé vers le bas. l'origine O de l'axe correspond à la position de départ de Félix Baumgartner. Ce dernier est supposé en chute libre dans cette partie. En appliquant la deuxième loi de Newton, donner l'expression de l'accélération subie par F. Baumgartner. Lors d'une chute libre az(t) = g. En déduire l'expression de la vitesse en fonction du temps. La vitesse est une primitive de l'accélération et la vitesse initiale est nulle, vz(t) = gt. Montrer que l'équation horaire du mouvement de F Baumgartner est donnée par z(t) = ½gt2. La position est une primitive de la vitesse et la position initiale est l'origine de l'axe, z(t) = ½gt2. Calculer l'instant auquel le reord de vitesse v = 1341,9 km/h a été atteint. 1341,9 / 3,6 = 372,75 m / s ; t = v / g = 372,75 / 9,75 =38,2 s. Après quelle distance parcourue, ce record a-t-il été ateint ?. d =0,5*9,75 *38,22 = 7,11 km. Quelle serait alors l'altitude de F. Baumgartner ? 39,0 -7,11 =31,9 km. . . Chute réelle et record de vitesse. Le graphe ci-dessous donne l'évolution de la vitesse en chute réelle en fonction du temps. 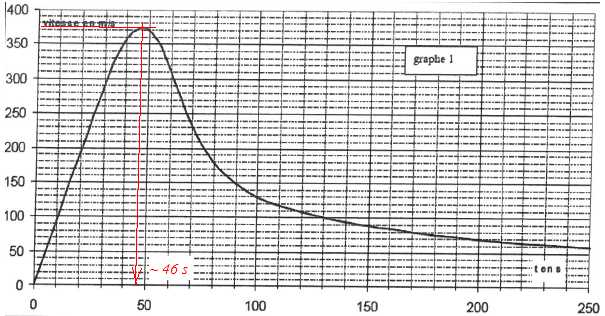Le graphe 2 donne l'évolution de l'altitude de F.Baumgartner en fonction du temps, enregistrée à l'aide de 4 balises GPS placées dans sa combinaison. Quelle est la valeur de la vitesse record en m / s ? A quel instant et à quelle altitude a-t-il réellement atteint cette vitesse ? 1341,9 / 3,6 = 372,75 m / s ; t ~416 s ; altitude voisine de 30 km. Le terme de chute libre, durant le première phase, est-il rigoureux ? D'après le graphe 1, la courbe est un segment de droite entre t=0 et t=40 s. La chute est donc libre. Par contre entre 40 et 46 s, la courbe n'est pas une droite et la chute n'est plus libre. Quelle est la vitesse du son au moment où la vitesse maximale est atteinte ? v=372,75  /1,24 =300,2 ~300 m/s. Quelle est la température de l'air à cette altitude ? v = (402 T)½ ; T = v2 / 402 = 300,22 /402 =224 K ou 224-273 = -48,8°C. Chute réelle et énegies. Donner l'expression de l'énergie cinétique et préciser les unités de chaque terme. Ec = ½mv2 avec Ec en joule, masse m en kg, vitesse v en m/s. Donner l'expression de l'énergie potentielle et préciser les unités de chaque terme. Ep = mgz avec Ep en joule, masse m en kg, g en ms-2, altitude z en mètre. Donner l'expression de l'énergie mécanique de baumgartner durant sa chute. E = Ec+Ep = ½mv2 + mgz, l'origine de l'énergie potentielle est prise au niveau du sol. Calculer la variation de l'énergie mécanique de Baumgartner entre les instants t1 = 60 s et t2 = 80 s et conclure. Les graphes donnent v(t1) = 300 m/s, v(t2) = 180 m/s, z(t1) = 25 000 m, z(t2)=20 000 m. Masse de Baumgaetner et de sa combinaison m = 110 kg. E(t1) = 110(0,5 *3002 + 9,75 *25000)=110(45000 +243750)=3,18 107 J. E(t2) = 110(0,5 *1802 + 9,75 *20000)=110(16200 +243750)=2,32 107 J. E(t2) -E(t1) = -8,6 106 J. L'énergie mécanique diminue du travail des frottements. Les frottements subis par Baumgartner peuvent être assimilés à une force notée f. Donner l'expression littérale du travail de la force f en fonction de sa valeur f et de la distance parcourue, notée h, par Baumgartner entre les instants t1 et t2. Travail résistant des frotements : W = - f h. Calculer la valeur de f. f = -(E(t2) -E(t1) ) / h = 8,6 106 / 5000 =1,7 103 N. A l'aide de la deuxième loi de Newton, donner l'expression de l'accélération " a " subie par Baumgartner entre les instants t1 et t2 ; calculer sa valeur. Suivant un axe vertical, orienté vers le bas : mg-f = ma ; a = g-f / m =9,75 -1,7 103 / 110 ~ -5,9 m s-2. Le signe de l'accélération est-il cohérent avec le graphe 1 ? Justifier. Entre les dates t1 et t2, le graphe 1 peut être assimilé à une droite décroissante. Le coefficient directeur de cette droite est négatif ; ce coefficient directeur est égale à l'accélération.   Le signe trouvé est donc cohérent avec le graphe 1. .

menu