Diffraction.
Concours orthoptie Nantes 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Quelle erreur commet Huyghens en comparant la propagation de la lumière à celle des ondes mécaniques ?
La lumière consiste en un mouvement de matière qu'il nomme éther. Une onde ne transporte pas de matière mais de l'énergie.
Citer deux propriétés générales des ondes que l'on peut retrouver dans le texte de Huyghens.
- La lumière se propage dans toutes les directions qui lui sont offertes.
- La propagation de la lumière depuis un objet lumineux ne se fait pas avec transport de matière.
Fresnel
a utilisé les rayons solaires pour réaliser son expérience de
diffraction. Une telle lumière est-elle polychromatique ou
monochromatique ? Justifier.
La lumière solaire comprend toutes les couleurs de l'arc en ciel ; elle est polychromatique.
Fresnel
exploite le phénomène de diffraction de la lumière par un fil de fer.
Le diamètre du fil de fer a-t-il une importance pour observer ce
phénomène ? Si oui, indiquer quel doit être son ordre de grandeur.
Pour observer un phénomène de
diffraction, le diamètre du fil de fer doit être de l'ordre de grandeur
de la longueur d'onde de la lumière.
On réalise une expérience de diffraction à l'aide d'un laser émettant une lumière monochromatique de longueur d'onde l.
A quelques centimètres du laser, on place successivement des fils
verticaux de diamètres connus. On désigne par "a" le diamètre du fil.
La figure de diffraction obtenue est observée sur un écran blanc situé
à une distance D = 1,60 m des fils. Pour chacun des fils on mesure la
largeur " L " de la tâche centrale. A partir de ces mesures, il
est possible de calculer l'écart angulaire q du faisceau diffracté.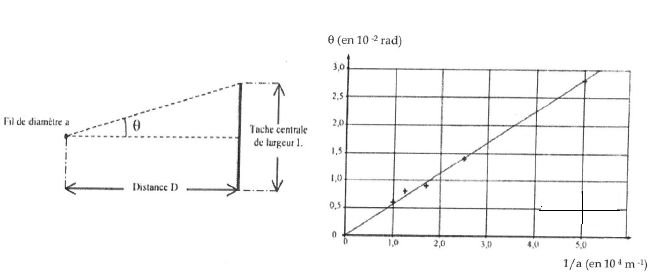
Influence du diamètre du fil sur la largeur de la tâche centrale de diffraction.
L'angle q étant petit, on a la relation q ~tan q, avec q en radian. Donner la relation entre q, L et D.
tan q ~ q ~½L / D.
On rappelle la relation q = l /a. Préciser les unités de l et a.
l et a s'expriment en mètre.
Montrer que la courbe obtenue est en accord avec l'expression de q. Calculer la longueur d'onde l.
L'écart angulaire est proportionnel à l'inverse du diamètre des fils. La courbe q = f(1/a) est une droite passant par l'origine, de pente égale à l.
Pente de la droite : 3,0 10-2 / (5,3 104) ~5,7 10-7 m ; l = 0,57 µm.
|
| .
. |
|
|
Influence de la longueur d'onde sur la largeur de la tâche centrale.
Quatre figures de diffraction sont obtenues avec 4 lasers différents.

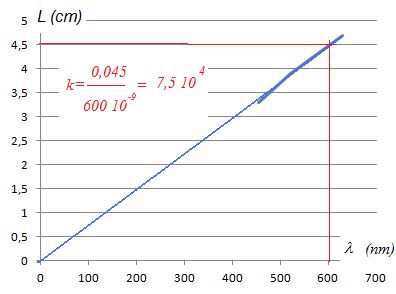
Tracer L = f(l). Montrer que L = k l et calculer la valeur expérimentale de k.
|
|
|
La courbe est une droite passant par l'origine. l et L sont proportionnelles.
Trouver la relation entre L, D, a et l.
En déduire la relation théorique de k et calculer la valeur théorique
de k. Calculer l'écart relatif entre les deux valeurs de k et conclure.
q ~½L / D et q = l /a ; par suite : L = 2 l D / a.
k = 2D/a 2*1,60 / (40 10-6) =8,0 104.
Ecart relatif : (8-7,5) / 8 ~0,062 ( 6,2 %).
Les deux valeurs sont en accord, la pente de la droite est déterminée de manière peu précise.
Si on envisageait de réaliser la même étude expérimentalement en
utilisant une lumière blanche, on observerait des franges irisées.
Justifier succinctement l'aspect irisé de la figure observée.
Chaque radiation de la lumière polychromatique donne un
système de diffraction dont la largeur de la tache centrale est
proportionnelle à la longueur d'onde. Au centre de la tache toutes les
radiations sont présentes ( couleur blanche) ; le bord de la tache
centrale est orange-rouge, le bleu étant absent.
|
|