Le curling. Concours orthoptie Rennes 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . Le Curling est un sport de précision qui consiste à placer des pierres taillées et polies le plus près possible du centre d’une cible. Le jeu se déroule sur une piste de glace parfaitement horizontale. Dans un premier temps, le joueur communique un mouvement à la pierre en la faisant glisser sur la glace. Puis il doit la lâcher, la pierre continue alors de glisser. Le but est que la pierre s’arrête le plus près possible du centre de la cible, elle-même horizontale et imprimée juste sous la glace. Données : la masse d’une pierre est m = 20,0 kg, l’intensité de la pesanteur est g = 9,81 m.s-2. Première partie : mise en mouvement de la pierre. Dans cette première partie, on néglige les frottements. Pour mettre en mouvement la pierre, le joueur la saisit par la poignée  et applique une force horizontale constante pendant 2,00 s puis il la lâche. Faire un schéma (sans souci d’échelle) représentant les forces qui s’applique sur la pierre pendant cette phase. Caractériser, en le justifiant, le mouvement de la pierre. 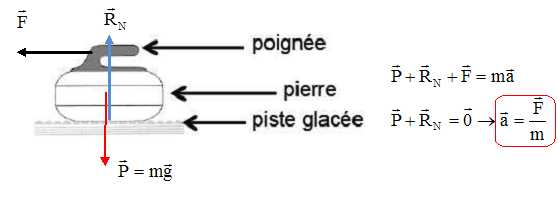Le mouvement de la pierre est rectiligne uniformément accéléré.  La force qu’exerce le joueur a pour valeur F = 35,0 N. Quelle est la valeur de l’accélération au début de la mise en mouvement de la pierre ? a = F / m = 35,0 / 20,0 = 1,75 m s-2.  Quelle est la vitesse de la pierre au moment où le joueur la lâche ? v = at +v0 avec v0 = 0 ; v(t=2)=1,75*2,00 = 3,50 m s-1. Quelle distance a parcouru la pierre au cours de cette phase ? x0 =  ½at2 = 0,5 *1,75 *22 =3,5 m. . . Deuxième partie : choc avec une autre pierre. Une fois que le joueur a lâché la pierre (notée A), celle-ci a une trajectoire en ligne droite le long de l’axe Ox, jusqu’à ce qu’elle heurte une autre pierre (notée B) initialement à l’arrêt. Juste avant le choc, la vitesse de la pierre A a pour valeur viA= 2,90 m.s-1. Juste après le choc, la vitesse de la pierre A a pour valeur vfA= 1,72 m.s-1. Avant le choc, la pierre B est immobile et juste après, elle a une vitesse de valeur vfB= 2,16 m.s-1. Par rapport à la direction initiale de l’axe Ox, les directions sont déviées de a= 48° pour la pierre A et de ß = 36° pour la pierre B.   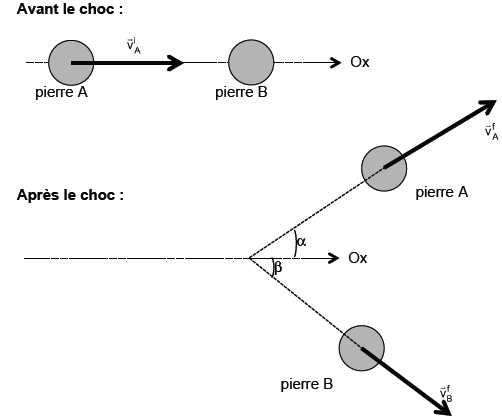À une distance d = 10,0 m avant le choc, la pierre A a une vitesse de valeur vA = 3,15 m.s-1. Expliquer pourquoi on ne peut pas négliger les frottements. Calculer la valeur de la force de frottement supposée constante pendant ces 10,0 m. 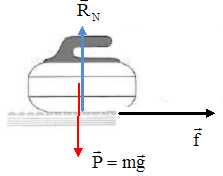La vitesse de la pierre diminue ; l'énergie cinétique de la pierre décroît du travail des frottements. ½m(viA2-vA2)= -f d. f = ½m(vA2-viA2)/ d=0,5 * 20,0 (3,152-2,902) / 10,0=1,5125 ~1,51 N. Déterminer la quantité de mouvement du système constitué des deux pierres juste avant le choc. pi=m viA=20*2,90 = 58,0 kg m s-1.  La quantité de mouvement se conserve-t-elle au cours du choc ? On justifiera par des calculs précis et détaillés. 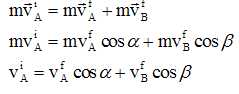2,90 =1,72 cos48 + 2,16 cos 36 ; 2,90 = 1,1509 +1,7475 ; 2,90 ~ 2,898. La quantité de mouvement se conserve au cours du choc.  Montrer que de l’énergie mécanique est perdue au cours du choc. Que devient cette énergie ? L'énergie potentielle est constante ( cette constante peut être prise  égale à zéro ), le mouvement se déroulant sur un plan horizontal. Energie mécanique avant le choc : ½m viA2 = 10*2,902 =  84,1 J. Energie mécanique après le choc : ½m vfA2+ ½m vfB2= 10 *1,722 + 10 *2,162= 76,2 J. La diminution d'énergie cinétique se retrouve sous forme d'énergie thermique. . Troisième partie : après le choc. Après le choc, la pierre A a pris la direction du centre de la cible qui se situe à la distance L = 18,5 m.  La pierre peut-elle s’immobiliser au centre de la cible ? La vitesse de la pierre diminue et doit s'annuler au centre de la cible ; l'énergie cinétique de la pierre décroît du travail des frottements. ½m(0-vfA2)= -f x. x =½mvfA2 / f = 0,5*20*1,722 / 1,5125 =19,6 m. Cette valeur est différente de L=18,5 m : la pierre ne s'immobilise pas au centre de la cible.

menu