Concours
ergothérapie Berck 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Satellite de Jupiter.
La
planète Jupiter est entourée de nombreux satellites parmi lesquels se
trouvent Europe, Ganymède, Io et Callisto. On se place dans le
référentiel jupiterocentrique supposé galiléen.
La trajectoire des chacun des satellites étudiés est considérée comme circulaire.
Le graphe ci-dessous est la représentation de l'évolution du carré de
la période T des satellites de Jupiter en fonction du cube du rayon r
de leur orbite. L'équation de la courbe obtenue est indiquée dans le
cadre. On donne G = 6,67 10-11 m3 kg-1 s-2.
p2 ~10 ; 3,12 *6,67 ~21.
Calculer la masse M ( x 1027 kg) de Jupiter.
1,9 ; 2,5 ; 4,2 ; 6,1 ; 8,4 ; aucune réponse exacte.
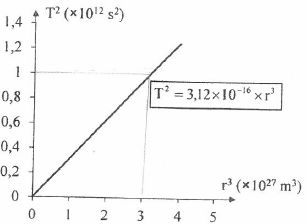
3è loi de Kepler : T2 = 4p2/(GM) r3.
4p2/(GM) = 3,12 10-16 ; M = 4p2/(3,12 10-16 G).
M ~4*10 / (3,12 10-16 *6,67 10-11) =40 / 21 1027 ~1,9 1027 kg.
Déviation des électrons par un champ lectrique.
Un faisceau homocinétique d'électrons pénètre à la date t=0, en un point O d'un condensateur plan, avec une vitesse v0
de direction horizontale. Le point O est équidistant des deux plaques
planes, parallèles et horizontales A et B du condensateur.
On applique une tension UAB entre les deux plaques. Il règne
alors un champ électrostatique uniforme de valeur E entre ces deux
plaques. Les électrons sortent du champ électrostatique créé par le
condensateur en un point S d'abscisse xS = D. On néglige le poids de l'électron devant la force électrique.
On donne v0 = 3,0 107 m/s ; D = 10 cm ; d = 5 cm ; UAB = -9,1 102 V.
e = 1,6 10-19 C ; masse de l'électron m = 9,1 10-31 kg.
Valeur du champ électrostatique à l'intérieur d'un condensateur : E = |UAB| / d.
On propose ci-dessous différentes expressions pour l'équation
cartésienne de la trajectoire d'un électron entre les plaques du
condensateur. Quelle est l'expression exacte ?
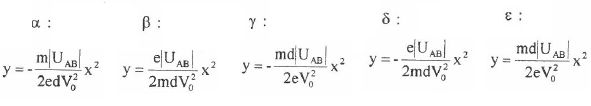
 Réponse : d Réponse : d.
|
| .
. |
|
|
Déterminer la valeur de l'ordonée yS ( en cm) du point de sortie S du condensateur plan..
-4,5 ; -1,8 ; 0 ; 1,8 ; 4,5 ; aucune réponse exacte.
xS = 0,10 m ; yS = -1,6 10-19 *9,1 102*0,12 / (2*9,1 10-31*0,05 *9,0 1014) .
yS = -1,6 *9,1 /(2*9,1*0,05*9,0) 10-2 =-1,6 /(2*5*9) = -1,6 / 90 ~ -0,018 m = - 1,8 cm.
Sonar.
Un
sonar est utilisé pour mesurer la profondeur h d'un fond marin. Un bref
signal ultrasonore est émis depuis le sonar embarqué par le bateau. Le
signal ultrasonore se propage verticalement dans l'eau de mer et se
réfléchit sur le fond marin. Le sonar capte le signal ultrasonore au
bout d'une durée Dt = 320 ms après son émission.
Célérité desultrasons dans l'eau de mer c =1,50 103 m/s.
Déterminer la profondeur h ( en m).
240 ; 320 ; 480 ; 540 ; 960 ; aucune réponse exacte.
2h = c Dt ; h = cDt / 2 =1,50 103 *0,160 = 240 m.
|
|
|
|
Pendule simple.
Un
pendule simple est constitué par un solide ponctuel P de mase m, fixé à
un fil inextensible de longueur L et de masse négligeable. On écarte le
pendule ainsi formé d'un angle q0
de la verticale et on l'abandonne sans vitesse initiale. Une étude
informatisée a permis d'obtenir le graphe ci-dessous donnant les
variations de l'énergie cinétique du pendule simple en fonction du
temps. On prendra pour niveau de référence de l'énergie potentielle de
pesanteur Epp la position d'équilibre du solide ponctuel.
m = 200 g ; q0 = 11,5 ° ; cos 11,5 = 0,98.
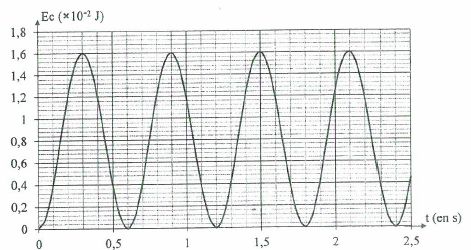
Parmi les affirmations suivantes, combien y en a t-il d'exactes ?
- L'amortissement des oscillations est négligeable pendant la durée de l'acquisition informatique. Vrai.
La vitesse maximale au passage à la position d'équilibre reste constante.
- L'énergie mécanique du pendule simple a pur valeur EM = 1,6 mJ. Faux.
Au passage à la position d'équilibre, l'énergie mécanique est sous forme cinétique. Le graphe indique 1,6 10-2 J = 16 mJ.
- L'énergie cinétique maximale a pour expression Ec max = mgL(1-cosq0) = ½mv2max. Vrai.
L'énergie mécanique initiale est sous forme potentielle et vaut : mgL(1-cosq0).
A la position d'équilibre, l'énergie mécanique est sous forme cinétique et vaut : ½mv2max.
Conservation de l'énergie mécanique : mgL(1-cosq0) = ½mv2max.
- La vitesse maximale du solide est égale à 0,4 m/s. Vrai.
½mv2max = 0,016 ; v2max = 0,016 *2 /0,200 = 0,16 ; vmax = 0,4 m/s.
- Le solide ponctuel atteint cette vitesse maximale à la date t = 0,6 s. Faux.
Période de l'énergie cinétique : 0,6 s.
Période des oscillations T = 1,2 s.
Date du premier passage à la position d'éuilibre : 0,25 T = 0,3 s.
Calculer la longueur L du fil ( en m).
0,3 ; 0,4 ; 0,5 ; 0,6 ; 0,7 ; aucune réponse exacte.
T = 2 p ( L/g)½ = 1,2 ; L =gT2 /(4p2)~10*1,44 /(4*10) = 0,36 m ~0,4 m.
Lentille convergente.
Un objet AB de hauteur 1,0 cm est placé devant une lentille mince
convergente de vergence C. Cet objet réel se trouve à 10 cm devant le
centre optique O de cette lentille. L'objet AB, assimilable à un
segment, est perpendiculaire à l'axe optique de la lentille et le point
A est situé sur l'axe optique. La lentille donne de cet objet une image
A'B' virtuelle, de même sens que l'objet et de 4,0 cm de hauteur.
Déterminer la vergence C ( en dioptrie) de cette lentille.
4,0 ; 5,5 ; 7,5 ; 10 ; 12 ; aucune réponse exacte.
La lentille fonctionne en loupe et le grandissement vaut 4,0 1,0 = 4,0.
Formule de conjugaison : 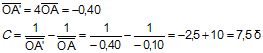
Relativité restreinte.
Un électron se déplace à la vitesse v par rapport au référentiel
terrestre associé à un laboratoire. On rappelle la relation de
dilatation temporelle : Dtm = g Dtp avec Dtm : durée mesurée et Dtp : durée propre. g =(1-v2/c2)-½ = 3,0
Déterminer la vitesse de l'électron, exprimée en fonction de la célérité c de la lumière dans le vide.
0,25 c ; 0,50 c ; 0,75 c ; 0,82 c ; 0,94 c ; aucune réponse exacte.
1 / 9 = 1-v2/c2 ; v2/c2 =1-1/9 =8/9 ; v / c ~0,94 c.
|
|
|
|