Trajectoire d'un électron. Concours Audioprothèsiste Paris 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . Un électron de masse m et de charge électrique –e arrive avec une vitesse de valeur v1 (assez faible pour qu’on ne prenne pas en compte d’effets relativistes) au point O. Il pénètre alors dans une région séparée par deux grilles horizontales entre lesquelles règne un champ électrostatique uniforme vertical ascendant de valeur E. Les deux grilles sont séparées d’une distance d. 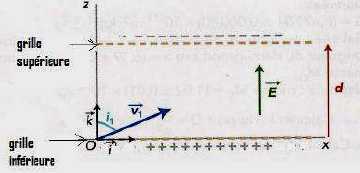Le référentiel d’étude est le référentiel du laboratoire supposé galiléen. Quelles sont les forces qui agissent sur l’électron pendant son trajet dans la zone entre les deux plaques ? Donner leurs caractéristiques. Poids de l'électron, vertical, vers le bas, valeur mg. Force électrique, verticale, vers le bas, valeur eE. Montrer, en calculant les ordres de grandeur des forces en action, que l’on peut négliger le poids de l’électron (ce que l’on fera dans toute la suite de l’exercice). Données : m = 9,11 10-31 kg ; e = 1,6 10-19 C ; E = 1000 V m-1 ; g = 9,81 N kg-1. mg = 9,11 10-31 *9,81 = 8,94 10-30 N. eE =1,6 10-19 *1000 = 1,6 10-16 N, trés supérieur au poids. Aucune autre application numérique ne sera exigée dans la suite de l’épreuve. En utilisant les lois appropriées, établir les équations horaires du mouvement de cet électron sachant que le vecteur v1 fait un angle i1 par rapport à l’axe vertical Oz. Accélération ( 0 ; -eE/m ) ; vitesse initiale : (v1 sin i1 ; v1 cos i1 ). Vitesse : (v1 sin i1 ; -eE/m t +v1 cos i1 ). Position : ( x = v1 sin i1 t ; z = -½eE/m t2 +v1 cos i1 t. Etablir l’équation cartésienne de la trajectoire (expression littérale). t = x / (v1 sin i1) ; repport dans z : z = -½eE/m x2 / (v1 sin i1)2+x / tan i1. . . Quelle est la nature de la trajectoire de l’électron ? Arc de parabole.  Dans le cas où il n’atteindrait pas la grille supérieure, représenter sur un schéma que vous aurez sommairement reproduit, l’allure de sa trajectoire ainsi que le vecteur vitesse au sommet S de la trajectoire. Au sommet de la trajectoire, la composante verticale de la vitesse est nulle. . Déterminer à l’aide de la question précédente les coordonnées du vecteur vitesse en S. Vitesse en S : (v1 sin i1 ; 0 ). En déduire l’expression littérale de la date tS à laquelle l’électron atteint le point S. -eE/m tS+v1 cos i1 = 0 ; tS = mv1 / (eE)cos i1. Donner l’expression littérale de l’ordonnée zS du sommet de la trajectoire. zS =-½eE/m (mv1 / (eE)cos i1)2 +v1 cos i1 mv1 / (eE)cos i1. zS =½m / (eE) v21 cos2i1. Quelle condition doit respecter la valeur E du champ électrostatique pour que l’électron atteigne la région au-dessus de la grille supérieure (expression littérale)? zS doit être supérieure ou égale à d. d = ½m / (eE) v21 cos2i1 ; 2d e2E2 =mv21 cos2i1 ; E2 =mv21 cos2i1  / (2d e2). Emini =v1 cosi1  / e (m / (2d))½. Dans ce cas là, quel sera alors le mouvement ultérieur de l’électron dans cette région ? L'électron n'étant soumis à aucune force sera animé d'un mouvement rectiligne uniforme. L’électron traverse la grille avec une vitesse v2. On note i2 l’angle entre ce vecteur et la verticale. 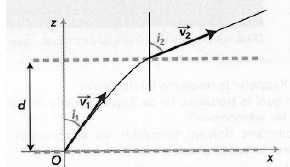La situation est représentée par le schéma suivant : Exprimer le sinus de l’angle i2 en fonction de v1, v2 , et du sinus de l’angle i1. La plaque supérieure est atteinte à la date t2 telle que : d = -½eE/m t22 +v1 cos i1 t2. Vitesse v2 : (v1 sin i1 ; -eE/m t2 +v1 cos i1 ) = (v2 sin i2 ; v2 cos i2). Par identification : v1 sin i1 =v2 sin i2. Au début du XXème siècle, on pouvait lire dans certains textes scientifiques que « dans certains dispositifs, les faisceaux d’électrons ont un comportement analogue à celui de rayons lumineux. Il est possible de reproduire les phénomènes de réflexion et de réfraction. » Justifier cette phrase. L'expression trouvée ci-dessus est analogue à la loi de Descartes pour la réfraction, en remplaçant les indices des milieux par les vitesses des électrons. .

menu