Analyse d'un son ; propagation d'une onde. Concours Audioprothèsiste Nancy 2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



.


.
.


Analyse d'un son émis par un instrument à vent.
Un trompettiste joue une note devant un microphone relié à un ordinateur muni d’un système
d’acquisition des données. On obtient à partir de l’enregistrement le spectre en fréquence de la
note jouée.

 S’agit-il d’un son pur ? Justifier votre réponse.
Le spectre compte plusieurs harmoniques : il ne s'agit pas d'un son pur.
Quelle est la valeur de la fréquence du fondamental ?
916 / 2 =458 Hz.
Calculer la fréquence du troisième harmonique.
458 *3 = 1374 Hz.
On représente ci-dessous l’enregistrement deux autres notes jouées par une trompette et
par un diapason séparément.

Attribuer à chaque graphique l’instrument adéquat en justifiant.
A : le diapason émet un son pur sinusoïdal.
B : la trompette émet un son complexe.
Déterminer la fréquence du fondamental de la note jouée par la trompette.
Période T = 0,002 s ; fréquence du fondamental : f0 = 1/T = 1/0,002 = 500 Hz.
On donne l’expression du niveau sonore L (exprimé en décibels notés dB) associé à une onde
sonore d’intensité acoustique I (W.m-2), L = 10 log( I / I0) où I0 représente l’intensité sonore de
référence égale à 1,0 × 10–12 W·m–2. Compléter le tableau suivant :
I (W.m-2) 100 10-9
 1,0 10-6
 31,6 10-5
 3,16 10-2
L(dB)
 50
 60
 85
 105
.
.
.





Une trompette génère en moyenne une intensité sonore I = 1,0 × 10–3 W.m–2.
Calculer le niveau sonore en dB auquel est exposé le trompettiste.
L = 10 log (1,0 10-3 / 10-12) = 90 dB.
Quand plusieurs sources sonores sont actives, le niveau sonore total en décibel (dB) est obtenu en sommant les intensités acoustiques (W/m2) respectives de chaque source.
Quel est le niveau sonore total en décibel quand :
- 2 trompettes jouent en même temps ?
I = 2 ,0 10-3 W m-2 ; L = 10 log (2,0 10-3 / 10-12) = 93 dB.
- 10 trompettes jouent en même temps ?
I = 1 ,0 10-2 W m-2 ; L = 10 log (1,0 10-2 / 10-12) = 100 dB.

.
Propagation d'une onde.
Pour mesurer la célérité d’un signal transversal le long d’une corde, on utilise deux cellules photoélectriques A et B, distantes de 2 m et reliées à un chronomètre électronique ainsi que le montre la figure suivante.

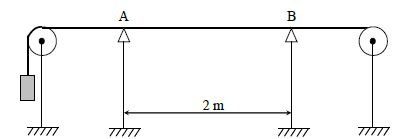
Il est possible de faire varier la tension de la corde (force exercée par la masse suspendue) et de mesurer la valeur T de cette tension. On peut également utiliser des cordes de masses linéiques différentes. La masse linéique d’une corde est le rapport de sa masse à sa longueur. Par exemple, si la masse linéique d’une corde est µ = 0,1 kg.m-1, la masse de 1 m de cette corde est 0,1 kg.
Expliquer succinctement le principe de l’expérience permettant de mesurer la célérité c du signal transversal le long d’une corde.
La distance AB est connue. Pour déterminer la durée de la propagation du signal entre A et B, la première cellule photoélectrique déclenche le chronomètre au passage du signal, tandis que la seconde cellule provoque l'arrêt du chronomètre au passage du signal.
Donner l’expression littérale de la relation qui lie la durée Dt de la propagation du signal entre A et B, la distance d qui sépare A et B et la célérité c du signal.
d = c Dt.
Au cours d’une première série d’expérience, la masse linéique de la corde est µ = 0,1 kg.m-1. On mesure la durée Dt de propagation du signal entre A et B pour différentes valeurs de la tension. Compléter la troisième ligne du tableau.
T(N)
 40
 20
 15
 10
Dt (s)
 0,10
 0,14
 0,16
 0,20
c ( m/s)
 2 / 0,10 = 20
 2 / 0,14 =14,2 ~14
 2 / 0,16 =12,5 ~13
 2 / 0,20 = 10
c / T½
 20 / 40½ = 3,16
 14,2 / 20½=3,17
 12,5 / 15½=3,23
 3,16

La célérité est-elle une fonction croissante de la tension de la corde ? Oui.
La célérité est-elle une grandeur proportionnelle à la tension de la corde ? Non.
La dernière ligne du tableau montre que la célérité est proportionnelle à la racine carré de la tension de la corde.
Au cours de la seconde série d’expérience, la tension de la corde est T = 40 N. On mesure la durée Dt de propagation du signal entre A et B pour différentes cordes
Compléter la troisième ligne du tableau.
µ(kg / m)
 0,10
 0,40
 1,6
 1,0
Dt (s)
 0,10
 0,20
 0,40
 0,32
c ( m/s)
 2 / 0,10 = 20
 2 / 0,20 =10
 2 / 0,40=5
 2 / 0,32 = 6,25
c x µ½
 20 *0,10½ = 6,3
 10*0,40½=6,3
 5*1,6½=6,3
 6,25*1,0½=6,25

Quelle est la grandeur qui est caractéristique de chacune des cordes ?
La masse linéique caractérise chaque corde.
La célérité est-elle une fonction croissante de la masse linéique de la corde ? Non.
D'après la dernière ligne du tableau, la célérité est inversement proportionnelle à la racine carrée de la masse linéique.
On souhaite vérifier que la valeur de la célérité du signal le long de la corde est donnée par la relation suivante : c = (T/µ)½.
Montrer que cette relation ) est cohérente avec les réponses précédentes.
 Montrer par analyse dimensionnelle que la grandeur (T/µ)½ est homogène à une vitesse.
Une force est une masse fois une accélération ; une accélération est une longueur divisée par le carré d'un temps :
[T] = M L T -2 ; [µ]= M L-1 ;  [T / µ] = L2 T -2 ; [(T / µ)½] = L T -1.
Vérifier, à partir d’un exemple numérique de la seconde expérience, que cette relation  permet de retrouver par le calcul la valeur de c obtenue expérimentalement.
(40 / 0,10)½ =20 m/s.

.


  

menu