Projectile,
spectrométre de masse, satellite, travail, pendule, transfert
thermique. Concours Puissance
11.
2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
8. Le
lancer du poids.
Un poids de masse m = 6,0 kg est lancé d'une hauteur h = 2,0 m au
dessus du sol avec une vitesse initiale v0 = 7,0
m/s faisant un angle a
avec l'horizontale. Le mouvement se fait dans un plan vertical et on
néglige les frottements de l'air.
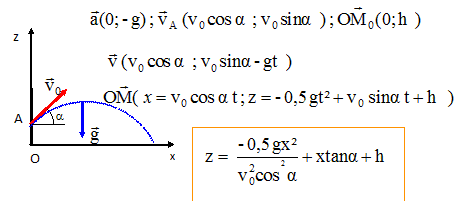 a) L'équation de la trajectoire est z = ½g x2
/(v0 cos a)2
+x tan a+
h. Faux.
a) L'équation de la trajectoire est z = ½g x2
/(v0 cos a)2
+x tan a+
h. Faux.
b)
Pour a
= 45°, l'équation de la trajectoire s'écrit z = - g x2
/v0 2 +
x +
h. Vrai.
c) Pour a =
45°, l'équation horaire sur la vitesse suivant Oz s'écrit vz
= -10 t +9,9. Faux.
vz
= -10 t +7 sin 45 =-10 t +4,9.
d) Pour a =
0°, le poids retombe à l'abscisse x = 4,4 m. Vrai.
0
= -0,102 x2 +2,0 ; x2 =2,0 /
0,102 = 20 ; x ~4,4 m..
9.
Spectrométrie de masse.
Des
ions de masse m, de charge q, sont accélérés par un champ électrique.
Ils pénètrent dans un champ magnétique B à la vitesse v. Ils adoptent
alors un mouvement circulaire uniforme. Seuls les ions possédant une
trajectoire de rayon R bien déterminé arrivent sur un détecteur (
plaque photographique ).
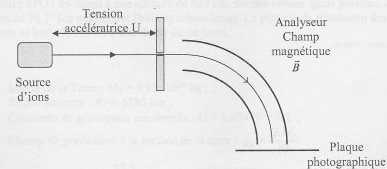
L'énergie cinétique de l'in qui pénètre dans l'analyseur est Ec=|q|U.
L'ion de poids négligeable est alors soumis à une force radiale
centripète d'intensité F = |q|v B.
B = 0,10 T ; U = 1000 V ; q = 1,6 10-19 C.
a) A l'entrée de l'analyseur, l'ion a une énergie cinétique
de 1,6 10-16 eV. Faux.
1,6 10-19 *1000 = 1,6 10-16 J ou 1,6 10-16 /(1,6 10-19) = 1000 eV.
b) La vitesse de l'ion est donnée par v =
(2|q| U / m)½. Vrai.
|q| U
= ½mv2 ; v2 = 2|q| U /m.
c) L'accélération est nulle car le
mouvement est uniforme. Faux.
La vitesse
change constament de direction. Seule sa norme est constante.
d) Le rayon de la trajectoire est donné par R = mv / (|q|B). Vrai.
L'accélération
est centripète de valeur an = F / m = |q|v B / m.
De plus an = v2/ R
; par suite : |q|v B / m
= v2/
R ; R = mv / (|q|B).
10.
Satellite Spot.
Il évolue à une altitude h=820 km sur des orbites quasi-polaires
circulaires. Sa période de révolution est de 101,4 min et le cycle
orbital dure 26 jours.
Masse de la terre M= 5,98 1024 kg ; rayon
terrestre R =6380 km.
7,1 x1,014~7,2 ; 22,3 ~7,1*3,14 ; 446 ~74*6.
a) Le satellite, lorsqu'il est en orbite circulaire, a un vecteur
accélération constant. Faux.
L'accélération
est centripète, sa valeur est constante mais sa direction change.
b) Le champ de gravitation à l'altitude du satellite a pour valeur g =
(R /(R+h))½g0, avec g0
valeur du champ de pesanteur à la surface de la terre. Faux.
g = GM /(R+h)2 ; g0 = GM/R2
; g = g0(R /(R+h))2.
c) Le rayon de
l'orbite a pour expression r= R+h= v2
/g. Vrai.
Valeur de l'accélération
centripète à l'altitude h : g = v2
/ r.
d) La vitesse du
satellite dans le référentiel géocentrique est v = 7,4 km/s. Vrai.
v T = 2p(R+h)
; v = 2p(R+h)
/ T = 2*3,14(6380+820) / (101,4*60) =6,28*7200 / (101,4*60).
v ~6,28 *7100*1,014 /(101,4*60 )~6,28*71 / 60 ~2*223 /60 ~
446 /60 ~ 7,4 km/s.
11.
Mouvement sur piste circulaire.
Un mobile S, de masse m =500 g, glisse sur un piste AB, quart de cercle
de rayon R = 40 cm. Il a été lancé de A sans vitesse initiale. On
néglige les frottements. B est l'origine de l'énergie potentielle.
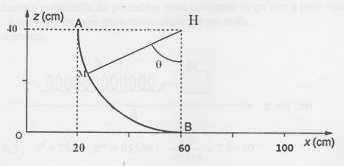
a) L'énergie
mécanique du mobile est constante entre A et B. Vrai.
b) Le travail
du poids sur le déplacement MB est W = mgR(1- sin q). Faux.
Différence
d'altitude entre M et B : h= R(1-cos q). Le
travail du poids est moteur en descente.
W = mg h = mgR(1-cos q)
c)
En M, où q
= 60°, l'énergie potentielle est égale à l'énergie cinétique. Vrai.
Energie
mécanique : E = mgR =0,50 *10 *0,40 =2,0 J ;
Energie
potentielle en M : mgR(1-cos60) =½mgR.
d) La vitesse
du mobile en M est v = 2,0 m/s. Vrai.
Energie cinétique en M : 1 = ½mv2
; v2 = 2/m = 2 / 0,5 = 4 ; v = 2 m/s.
|
| .
. |
|
|
12.
Pendule élastique horizontal.
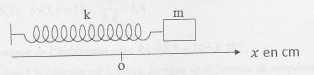
m = 2,0 kg ; équation horaire x(t) = 2,0 cos ( 10 t +½p),
avec x en cm, t en s.
L'énergie potentielle élastique est nulle à la position d'équilibre.On
néglige les frottements.
2p
=6,3 .
a) A la date t=0, le pendule se trouve à sa position d'équilibre. Vrai.
x(t=0) =2,0
cos (½p
)= 0.
b) A la date t=0, le pendule se déplace vers la droite avec une vitesse
de 20 cm / s. Faux.
v = x'(t) =
-20 sin( 10 t +½p) ; v(t=0) = -20 cm/s.
Le pendule
se déplace vers la gauche, en sens contraire de l'axe.
c) La période
des oscillations est T0 = 0,63 s. Vrai.
T0 = 2p / w avec w = 10 rad / s. T0 = 6,3 / 10 = 0,63 s.
d) L'énergie mécanique du système est E = 4,0 µJ. Faux.
A la
position d'équilibre, l'énergie mécanique est sous forme cinétique.
½mv2 = 0,5 *2 *0,22 =0,04 J.
|
.
|
|
13.
Isolation thermique.
On considère une habitation parallèlépipèdique de longueur L = 10,0 m,
de largeur l
= 10,0 m dont la hauteur des murs est H = 3,0 m. La capacité thermique
de cette habitation est C = 700 kJ K-1. La
résistance thermique de l'ensemble des parois ( murs + sol + toit ) est
Rth = r / s où r = 6,4 m2
K W-1 et s correspond à la surface totale des
parois en m2.
6,4 / 1,2 = 5,3 ; 5*3,6 = 18 ; 5 / 3,6 =1,4.
a) La résistance thermisue de l'habitation vaut Rth
= 5,3 10-2 W-1 K.
Faux.
s = 2((L+l )H + L l
)=2((10,0 +10,0) *3,0 +10,0 *10,0)=320 m2
; Rth
=6,4 / 320 = 2,0 10-2 W-1 K.
b) Le flux thermique dont l'habitation est le siège, lorsque la
différence de température entre l'intérieur et l'extrieur est de 10°C,
est de 5,0 102 W.
Vrai.
Flux
= 10 / Rth = 10 / 0,02 = 5,0 102 W.
c) Au bout
de 10 h, l'énergie perdue par l'habitation est de 18 MJ.
Vrai.
5,0 102
*10*3600 =1,8 107 J = 18 MJ.
d) L'énergie nécessaire pour obtenir une augmentation de température de
0,5 °C dans cette habitation est 0,35 MJ.
Vrai.
700*0,5 =350
kJ = 0,35 MJ.
14.
Freinage
d'une automobile.
Une auto de masse m = 1 tonne descend en roue libre une pente de 6 % à
la vitesse de 72 km/h. Le chauffeur freine et la voiture s'arrête en
100 m.
1 / 1,82 ~0,55 ; 1,82 / 3,5 =0,52
a) La force de freinage, parallèle à la route et supposée constante
vaut 2,6 kN. Vrai.
Variation de l'énergie cinétique
: v = 72 /3,6 = 20 m / s ; 0-½mv2 = -500 *202 = -2,0 105 J.
Travail
moteur du poids en descente : mgh = 1000 * 10 * 6 = 6,0 104 J.
Travail de
frottement + travail du poids = variation de l'énergie cinétique.
-100 f + 6,0 104
= -2,0 105 ; f = 2,0 103
+ 6,0 102 ~2,6 kN.
b)
A masse égale des disques et dans des conditions de freinage
équivalentes, la température des disques en carbone s'élève plus que
celle des disques en acier, mais la température acceptable pour le
carbone est plus élevée. Faux.
Cacier = 0,52 kJ kg-1 K-1
; Ccarbone
= 1,35 kJ kg-1 K-1 ;
Point de fusion : 1450 °C pour l'acier et >
3000 °C sublimation pour le carbone.
Elévation de
température des disques = énergie à dissipée / (masse des disques fois
capacité thermique des disques).
On suppose que 100 kJ sont dissipés au niveau d'un disque de 3,5 kg en
acier.
c) L'élévation de température est d'environ 55 °C. Vrai.
100 / (3,5 *0,52) =100 / 1,82 =
55°C.
d) La conductivité thermique n'a aucune influence sur la qualité des
freins. Faux.
|
15.
CAN.
Le schéma ci-dessous présente le principe de l'encodage d'un signal analogique. La durée du signal encodé est de 700 µs.
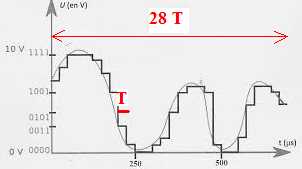
a) La fréquence d'échantillonnage est égale à 20 kHz. Faux.
T=700 10-6 / 28 s ; f = 1 / T =28 / (700 10-6)= 40 kHz.
b) Le pas de quantification est 0,31 V. Faux.
Pour un codage 4 bits : p =(Umax-Umin) / 24 = (10-0) / 16 ~0,62 V.
c) Le poids du signal encodé est de 112 bits. Vrai.
28 valeurs sont relevées ; chaque valeur est codée sur 4 bits.
d) La durée de transmission du signal est de 79,3 µs si le débit est 1,411 mégabits par seconde. Vrai.
112 /(1,411)=79,3 µs.
16. ADSL et atténuation.
Un utilisateur constate un débit binaire en téléchargement de 25 Mbits s-1. Le coefficient d'atténuation du câble est de 8 dB km-1.
a) La durée d'un élément binaire est d'environ 40 ns. Vrai.
1 / (25 106)=4 10-8 s = 40 ns.
b) La durée de transfert d'un fichier de 5 Go est d'environ 200 s. Faux.
5 Go = 5 109 *8 bits ; 8* 5 109 /(25 106) = 1,6 103 s.
Si l'émetteur et le récepteur sont distants de 500 m.
c) L'atténuation est de 4,0 dB. Vrai.
d) La puissance en bout de ligne est alors 4 fois plus faible qu'en entrée. Faux.
A = 10 log (Pentrée / P sortie) ; 0,4 = log (Pentrée / P sortie) ; Pentrée / P sortie = 100,4 = 2,5 ; P sortie =Pentrée / 2,5 = 0,4 Pentrée . |
|
|