Chimie
minérale ; titrage acide base. Concours
ITRF Rennes
2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
3.1 : Les structures cristallines (10
points)
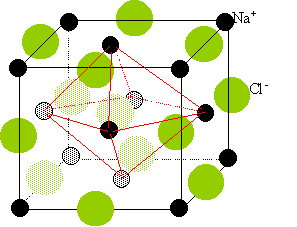
Sur le schéma ci-dessous, représenter avec le symbolisme proposé, la
maille cristalline du
chlorure de sodium. La symétrie est cubique, les ions Cl-
occupent les noeuds d'un réseau de
Bravais de type F et les ions Na+ occupent la
totalité des
sites octaédriques de la maille.
D eux réseaux cubiques à faces
centrées,
l'un d'ion Na+, l'autre d'ion chlorure Cl-.
Ces réseaux se déduisent l'un de l'autre par translation parallèle aux
arètes de la maille et de valeur égale à la moitié du coté de la maille.
Chaque ion est au centre d'un octaèdre, entouré de 6 ions de signe
opposé occupant les 6 sommets.
3.1-a : Calculer le
nombre de motifs
par maille de cette structure. (2 points)
Chaque ion
sodium situé au sommet compte pour 1/8 ème et chaque ion situé au
centre d'une face compte pour 1/6 éme ; total : 4 ions sodium par
maille.
Chaque ion sodium situé au milieu d'une arète compte pour 1 /4 et l'ion
central pour un ; total 4 ions chlorure par maille.
3.1-b
: Calculer le
paramètre de la maille de NaCl. (2 points)
Données : RNa+ = 0,99 10-10
m et RCl-
1,81 10-10 m.
a = 2(RNa++RCl-)=
2(0,99 +1,81) 10-10 =5,6 10-10
m.
3.1-c:
Calculer en
g.cm-3 la masse volumique de NaCl. (3 points)
Données : N = 6.02 1023 ; MNa
= 23 g/mol ; Mcl
= 35,5 g/mol
Masse d'une maille : 4(23+35,5) /(6,02 1023)=3,887
10-22
g.
Volume d'une maille : a3 = (5,6 10-10
)3=1,756
10-28 m3 =1,756 10-22
cm3
.
Masse volumique : 3,887 10-22
/ (1,756
10-22) =2,21 g cm-3.
3.1- d:
Calculer la compacité de la maille NaCl sachant qu'elle est définie
comme le rapport du
volume des
atomes de la
maille sur celui de la maille cubique. (3 points)
Volume des ions sphériques par maille :
4 *4*3,14 /3(0,993 +1,813)
10-30 =
1,155 10-28 m3.
Compacité : 1,155
10-28 / (1,756 10-28)=0,66.
|
| .
. |
|
|
3.2 : L'absorption des
rayonnements
(5 points)
Les rayonnements électromagnétiques (visibles ou non) sont absorbés par
la matière suivant une loi de Beer-Lambert que l'on peut écrire comme
suit :
I = I0.exp(-µx)
I est l'intensité transmise à travers la matière, I0
est l'intensité
incidente, µ, qui dépend de la longueur d'onde du rayonnement, est le
coefficient d'absorption du matériau (en
cm-1) et x son épaisseur (en cm).
3.2-a :
Calculer le pourcentage de rayonnement transmis à travers une
feuille d'aluminium d'épaisseur 10-1 mm (µ =
129,6 cm-1). (2 points).
I / I0 = exp(-129,6 *0,01)=0,274 ( 27,4 %).
3.2-b
: Calculer le pourcentage de rayonnement transmis à travers une couche
d'air d'épaisseur 1,5 m (µ = 0.014 cm-1). (2
points)
I / I0 =
exp(-0,014 *150)=0,122 ( 12,2 %).
3.2-c : Quelle
configuration assure la meilleure protection à ce rayonnement ? (1
point)
Une épaisseur de quelques mm d'aluminium assure une bonne protection.
3.3 : Les
changements d'états (8 points)
3.3-a
: La température d'ébullition de N2 liquide est
de 77 K. Quelle est la valeur de cette température lorsqu'elle est
exprimée en °C ? (2 points)
77-273 = -196°C.
3.3-b
: Une bouteille de gaz industriel contient 40 litres de diazote liquide
sous une pression de 200
bars. Calculer le volume de N2 gazeux obtenu par
détente à la pression atmosphérique (1 bar).
Masse volumique du diazote liquide au point d'ébullition 0,81 kg / L.
Masse de diazote : 40*0,81 = 32,4 kg.
Quantité de matière en mole : 32,4 / 0,028 ~1,16 103
mol.
Volume sous 1 bar à 25°C : 1,16 103*24 =2,8 104
L.
3.3-c
On utilise ce
gaz comme gaz de balayage dans un four. Le débit choisi est de 2 litres
par heure. Combien de jours peut-on faire fonctionner ce four jusqu'à
épuisement de la bouteille de gaz ?
2,8 104 / 2 = 1,4 104
heures soit environ 580 jours.
|
|
|
|
3.3-d :
On donne le diagramme binaire solide-liquide suivant. Identifier sur le
diagramme les phases en présence dans les différents domaines.
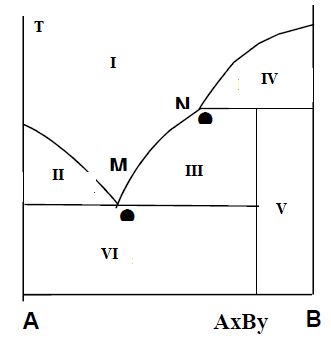
I : liquide ; II : liquide + A solide ; III : liquide + composé défini
AxBy solide ; IV : liquide + B solide ; V : B +AxBy solide ; VI : A
solide.
Le composé AxBy est-il à fusion congruente ? (1 point)
Non, fusion incongruente.
Que représentent les points M et N ? (1 point). M eutectique ;
N péritectique.
3ème
Partie : Chimie générale (50 points)
1-
pHmétrie (12 points)
On a réalisé 4 dosages (courbes A, B, C, D).
Solutions à titrer à votre disposition :
Acide chlorhydrique, Acide éthanoïque (pKa =
4,75), Acide sulfurique (pKa = 2.0), Acide
phosphorique (pKa1 =2,1 ; pKa2
=7,2 ; pKa3 =12,4 ), Hydroxyde de sodium,
Ammoniaque (pKa = 9.25 )
Titrants à votre disposition : Acide chlorhydrique, Hydroxyde de sodium
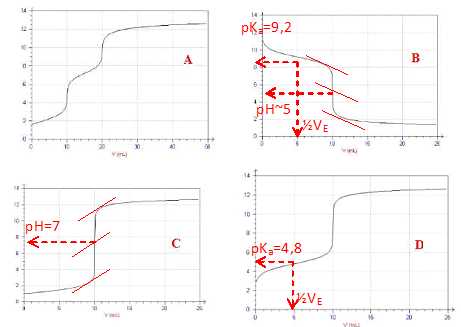
1.1
Donner la (les) solution(s) à titrer (prise séparément) et le titrant
pouvant correspondre aux 4 courbes à votre disposition.
A : solution titrée : acide phosphorique, titrant : hydroxyde de sodium.
B : solution titrée : ammoniac, titrant : acide chlorhydrique.
C : solution titrée : acide chlorhydrique, titrant : soude.
D : solution titrée : acide éthanoIque , titrant : soude.
1.2
: Pour le dosage de l’acide éthanoïque (c = 10-2
mol/L) par une base forte, quel est le pHattendu ?
1.2-a
: A la demi-équivalence. pH = pKa = 4,8.
1.2-b
: A V= 0 mL de la base versée. pH =½( pKa + log
c) =0,5(4,8+2)=3,4.
1.3 : On dispose de
100 mL d’acide éthanoïque à C=0,1 mol/L. Quelle masse d’éthanoate de
sodium faut-il ajouter pour préparer une solution tampon à pH= pKa
? (2 points)
[CH3COOH] =[CH3COO-]=0,1
mol/L. M(CH3COONa)=82 g/mol
n(CH3COO-) = 0,1*0,1 = 0,010 mol ; m =
0,010*82 = 0,82 g.
1.4 :
Quelles sont les propriétés des solutions tampons ? (2 points).
Une solution tampon modère les variations de pH suite à l'ajout modéré
d'acide fort ou de base forte, suite à une dilution modérée.
|
|
|
|