Autour du moteur à essence. Concours ITPE 2015

Autour du moteur à essence. Concours ITPE 2015

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

On donne le schéma global d'un moteur ditherme. On notera T_F et T_C respectivement les températures de la source froide et de la source chaude.

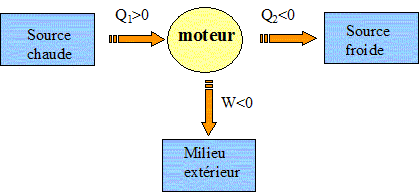
Donner en justifiant le signe de W.
Le système gagne de l'énergie à la source chaude, cède de l'énergie à la source froide et du travail au milieu extérieur.
Donner une relation entre W, Q₁ et Q₂.
Premier principe : sur le cycle : W+Q₁+Q₂=0 soit W= -(Q₁+Q₂).
On suppose le moteur réversible, démontrer que Q₁/T_C + Q₂/T_F =0.
Second principe : DS= S_échangée + S_créée= 0 avec S_créée= 0, pour un sytème réversible.
Q₁/T_C + Q₂/T_F = 0 ; Q₂/Q₁ = -T_F/T_C.
En déduire que W /T_F =Q₁[1/T_C-1/T_F].
W= -(Q₁+Q₂) ; W /T_F = -(Q₁/T_F+ Q₂/T_F) ;
W /T_F = Q₁ [ -1/T_F-Q₂/(Q₁T_F) ];
W /T_F = Q₁ [-1/T_F+1/T_C].
On définit l'efficacité thermodynamique e_c du moteur comme étant le rapport entre le travail fourni par le moteur et le transfert thermique reçu de la source chaude. Exprimer e_c en fonction de T_F et T_C.
e_c =|W| / Q₁ = 1- T_F/T_C.

Application au moteur à essence.
Le moteur à explosion est constitué d'un piston mobile dans un cylindre muni de soupape d'admission et d'échappement. On donne l'allure de son diagramme de Watt.

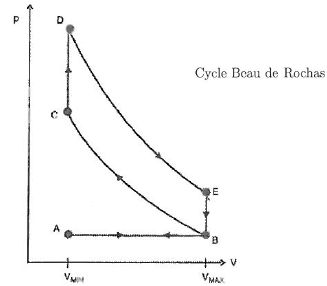
AB : admission isotherme et isobare du mélange initial ( air-carburant) considéré comme un gaz parfait de coefficient isentropique g = 1,40.
BC : compression, la soupape d'admission se ferme et le piston comprime le mélange jusqu'à ce que le volume du cylindre soit minimal V_C = V_min.
CD : une étincelle électrique enflamme le mélange. On suppose cette évolution isochore.
DE : détente jusqu'au retour du piston tel que le volume du cylindre soit maximal.
BA : la soupape d'échappement s'ouvre et libère les gaz de combustion.

..
.

Identifier le système. Qui joue le rôle de la source froide ?
Le système est constitué de l'air et du carburant. L'air extérieur constitue la source froide.
Expliquer pourquoi la portion AB ne représente aucun intérêt pour calculer le travail fourni par le système au cours d'un cycle.
Lors d'une transformation isobare et isotherme le travail mis en jeu est nul.
On note e l'efficacité thermodynamique du système. Montrer que : e = 1+Q₂/Q₁.
Q₁ : transfert thermique au cours de la transformation CD et Q₂ transfert thermique au cours de l'évolution EB.
e = |W| / Q₁ et W= -(Q₁+Q₂) ; e = (Q₁+Q₂) / Q₁ =1+Q₂/Q₁.
Exprimer la variation d'énergie interne U du système durant la phase CD en fonction de c_v ( capacité calorifique à volume constant du système), T_C et T_D.
L'évolution étant isochore, le travail mis en jeu est nul ; U = Q_CD+W_CD = Q_CD = c_v ( T_D-T_C).
En déduire l'expression de Q₁ en fonction de c_v , T_C et T_D.
Q₁ = c_v ( T_D-T_C).

.

Dans la suite du problème on admet que Q₁ = nR(T_D-T_C) / (g-1) et que Q₂ = nR(T_B-T_E) / (g-1) où n est la quantité de matière de gaz constituant le système.
Exprimer e en fonction de T_E, T_B, T_D,et T_C.
e=1+Q₂/Q₁ ; Q₂/Q₁ =(T_B-T_E) /(T_D-T_C) ; e = 1 +(T_B-T_E) /(T_D-T_C).
Les évolutions BC et DE sont isentropiques. En déduire que : T_C = T_B a^g-1 et T_D = T_E a^g-1 où a =V_max / V_min, taux de compression.
BC est une compression adiabatique réversible :T_C V_min^g-1 =T_B V_max^g-1.
T_C =T_B V_max^g-1 /V_min^g-1 = T_B a^g-1.
DE est une détente adiabatique réversible :T_D V_min^g-1 =T_E V_max^g-1.
T_D =T_E V_max^g-1 /V_min^g-1 = T_E a^g-1.
Exprimer e en fonction de a et g.
T_D-T_C = T_E a^g-1-T_B a^g-1 = (T_E-T_B)a^g-1.
(T_B-T_E) /(T_D-T_C) = - 1/a^g-1.
e = 1 +(T_B-T_E) /(T_D-T_C) = 1- 1/a^g-1.
Le tableau suivant donne la valeur de l'efficacité e pour différentes valeurs de a.

a
3
6
9
11

e
36 %
51%
58%
62%

Un exemple concret : la Peugeot 208 1.0 VTI.
Taux de compression 11 ; consommation à 120 km/h : 5,5 L de sans plomb pour 100 km ; vitesse à 3000 tours / min : 120 km/h.
On admettra pour simplifier que le moteur ne comporte qu'un seul cylindre. La température des gaz à l'admission est de 330 K. Calculer la température des gaz en fin de combustion.
T_B = 330 K ; T_C =T_B a^g-1 = 330 *11^0,4=861,13 K.
e = 1 +(T_B-T_E) /(T_D-T_C) ; 0,62 = 1+(330-T_E) / (T_D-861,13) ; 1-0,62 =0,38= (-330+T_E) / (T_D-861,13) ;
-0,38*861,13+0,38 T_D = -330+T_D /a^g-1 ; 330-327,23 =(-0,38+0,383215 )T_D ; T_D =865,6 K.
Le sans-plomb des moteur à essence est un hydrocarbure de grande masse molaire et de masse volumique 800 kg m^-3. Quelle est la masse de carburant injecté à chaque cycle à 120 km/h ?
Masse de carburant consommé aux 100 km : 5,5 10^-3 *800 = 4,4 kg.
Durée mis pour parcourir 100 km : 100/120*60 =50 minutes. Nombre de cycles pour 100 km : 3000*50 = 1,5 10⁵.
Masse de carburant injecté par cycle : 4,4 / (1,5 10⁵)=2,93 10^-5 kg = 29,3 mg.
Comparer l'efficacité de la 208 avec l'efficacité de Carnot e_c et conclure.
e_c = 1- T_F/T_C = 1-330 / 865,6 =0, 62.
L'efficacité réelle est proche de l'efficacité théorique de Carnot ( valeur maximale obtenue dans le cas de la réversibilité ) pour un taux de compression de 11.

.

menu