Etude d'une
microbalance à cristal de quartz.
Concours général 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Le quartz, de formule brute SiO2, est un matériau dur (7 sur l’échelle de Mohs), fragile et transparent, de masse volumique r = 2, 65.103 kg.m−3.
Le quartz est, en outre, un matériau piézoélectrique. Si on considère
un morceau taillé de cristal de quartz et que l’on impose une tension
électrique à ses bornes, le matériau réagit en subissant une contrainte
mécanique. Inversement, si l’on soumet le quartz à une contrainte
mécanique, une tension électrique apparait entre ses bornes.
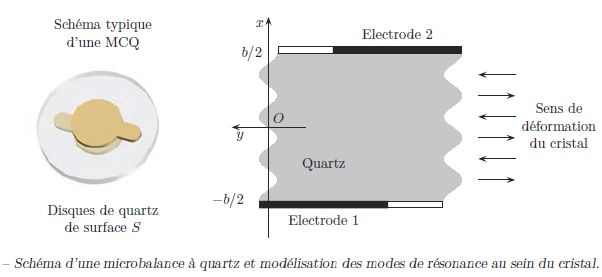
La
structure cristalline du quartz lui confère de très bonnes propriétés
de résonance. Si l’on applique une tension électrique alternative au
quartz à une fréquence proche de sa fréquence propre f0, on provoque l’apparition d’ondes progressives de cisaillement dans le cristal, analogues à des ondes sismiques, de célérité cq = 3340 m.s−1, dont l’amplitude peut devenir très importante et qui déforment le cristal.
On a représenté sur un exemple de microbalance à cristal de quartz (MCQ) et le type de résonance
observée lorsqu’une tension sinusoïdale de la forme U(t) = Um cos(2pt/T) est appliquée au cristal. Il
s’agit du même type d’ondes que celles observées sur une corde vibrante.
On considère une corde tendue horizontalement d’axe (Ox). Deux ondes
transverses s’y propagent en sens inverse l’une de l’autre, les
élongations transversales de ces ondes sont modélisées par les
équations :
y+(x,t) =Ym cos ( 2p(t/T -x / l)) et y-(x,t) =Ym cos ( 2p(t/T +x / l)+f)
Quelle relation existe-t-il, pour une onde progressive sinusoïdale entre T, l et cq ?
l = cq T.
Dans quel sens se propage l’onde y+(x, t) ?
L’onde y+(x, t) se propage de la gauche vers la droite.
Sachant qu’en tout point de la corde, et à tout instant, les déformations dues aux ondes s’additionnent, on admet que l’onde yr résultant de la superposition de y− et y+ s’écrit :
yr(x, t) = y−(x, t) + y+(x, t) = Y0 cos ( 2pt/T +½f) cos(2px/l +½f)
Déterminer l'expression de Y0.
Ym [ cos ( 2p(t/T -x / l) +cos ( 2p(t/T +x / l)+f) ]=2Ym [ cos ( 2pt/T +½f)cos(2px/l +½f)]
Par identification Y0 = 2 Ym.
Dans le cas du cristal de quartz, d’épaisseur b, on montre que la déformation transverse s’écrit :
yr(x, t) =Y0(x)cos ( 2pt/T +½f)
où Y0(x) = Y0 cos(2px/l +½f) représente l’amplitude de la déformation en un point d’abscisse x.
La symétrie de l’excitation du système impose que la déformation est nulle à tout instant en x = 0 et que son amplitude Y0(x) est maximale en x = ±b/2.
Déterminer la valeur de f.
Y0(x= 0) = Y0 cos(½f) =0 = cos (0,5 p) soit f =±p.
|
| ..
.. |
|
|
Montrer que les conditions limites en x = ±b/2 imposent une quantification des valeurs de la
longueur d’onde donnant lieu à un phénomène de résonance, celles-ci ne pouvant prendre que les valeurs : lp =2b /(2p+1) avec p appartenant à N.
Y0(x= ½b) =Y0 cos(pb/l ±½p)= Y0 cos(p(b/l ±½) = Ymax.
pb/l ±½p= 0+2kp ; b/l ±½= 2k ; l =b / (2k±0,5).
On note fq la fréquence de résonance fondamentale correspondant à p = 0. Calculer l’épaisseur b
du cristal donnant lieu à une fréquence fondamentale de 5, 00 MHz.
lp =2b = cq / fq =3340 /(5,0 106)= 6,68 10-4 m ; b = 3,34 10-4 m.
|
|
|
.
|
|
On
considère dans la suite du problème que le cristal de quartz est taillé
de manière à posséder une fréquence fondamentale de 5, 00 MHz.
On dépose à présent un film homogène de masse Mf de manière uniforme à la surface S du résonateur à quartz étudié ci-dessus. Dans le cas où Mf est négligeable devant Mq,
la masse du cristal de quartz résonant, Günter Sauerbrey montra en 1959
que la fréquence fondamentale du quartz était déplacée d’une quantité dfq vérifiant la relation :
dfq / fq = -Mf / Mq.
On introduit les masses par unité de surface mf =Mf /S et mq = Mq /S.
Exprimer mq en fonction de rq et b.
Mq =Sbrq ; mq =brq.
dfq / fq = -mf / mq =-mf / (brq) avec b = cq / (2fq).
dfq / fq = -2mf fq / (rq cq).
Calculer la valeur de mf donnant lieu à un décalage en fréquence de 1 Hz. On exprimera le résultaten ng.cm−2.
1/(5,00 106) = -2 mf *5,00 106 / (2,65 103 *3340) ; 2,00 10-7 = 1,13 mf ; mf =1,77 10-7 kg m-2 = 17,7 ng cm-2.
En considérant que la masse volumique du matériau déposé est d’environ 3.103 kg.m−3, estimer l’ordre de grandeur de l’épaisseur du dépôt. Commenter.
1,77 10-7 /(3.103)~ 6 10-11 m.
Outre
l’extrême sensibilité de cette méthode à la masse déposée, quels
avantages présentent l’utilisation d’une microbalance à quartz ?
Taille réduite du système, signal électrique facile à générer et à traiter.
Quels inconvénients doit-on cependant prendre en compte dans le cadre d’un dépôt multicouches ?
Il faut tenir compte de la différence d'impédance acoustique du dépôt multicouches.
|
|
|