Grillage de la
blende ; production du sulfate d'aluminium. Concours DGCCRF 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Un peu de nomenclature.
Le soufre se situe dans la 3è ligne et dans la 16è colonne de la classification périodique.
Décrire
brièvement la méthode de construction de la classification périodique
et en déduire la configuration électronique du soufre à l'état
fondamental
Les éléments sont
rangés par ordre croissant de leur numéro atomique. Chaque ligne
correspond au remplissage d'une couche électronique. Dans chaque
colonne les éléments ont la même structure électronique externe.
Dans l'état fondamental, la configuration électronique du soufre est : 1 s2 2s2 2p6 3s2 3p4.
En déduire les deux nombres d'oxydation les plus fréquement rencontrés pour l'élément soufre.
-II dans H2S et +VI dans H2SO4 ( +IV dans SO2 ).
Quel élément se situe dans la même colonne ? Oxygène.
Le soufre naturel est constitué de 4 isotopes stables dont deux présents en majorité : x % de l'isotope 32S et y % de l'isotope 34S.
La masse molaire de l'isotope 34 est de 33,968 g/mol et celle de
l'isotope 32 est de 31,972 g/mol. Calculer x et y sachant que la masse
molaire du soufre est 32,066 g/mol.
y = 100-x ; 33,968 (100-x) /100 +31,972 x /100 = 32,066.
3396,8 -33,968 x +31,972 x = 3206,6 ; 1,996 x = 190,2.
x = 95,29 % ; y = 4,709 %.
Définir l'électronégativité et comparer l'électronégativité du soufre et de l'oxygène..
L'électronégativité est l'aptitude que possède un atome à s'approprier le doublet de liaison l'associant à un autre atome. Le soufre est moins électronégatif que l'oxygène.
Ecrire les formes mésomères possibles du thiosulfate S2O32- et en déduire les formes les plus probables.
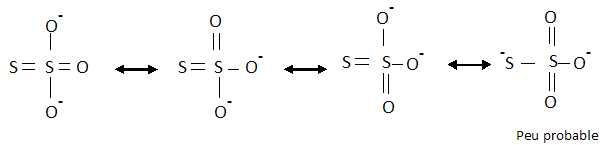
Diagramme E-pH.
On plonge une électrode de platine dans une solution de sulfure d'hydrogène H2S
aq ( c = 0,1 mol/L avec du soufre solide en suspension. On précise que
le sulfure d'hydrogène est présent sous sa forme soluble. Indiquer le potentiel de cette électrode. E°(S(s) / H2Saq) =0,14 V.
Quelles sont les espèces prédominantes en fonction du pH ? 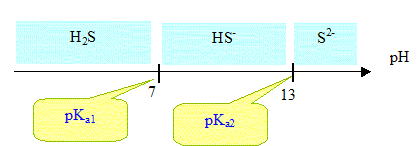
Tracer le diagramme E-pH en indiquant dans chaque domaine la nature de l'espèce à considérer.
S(s) +2e-+2H+ = H2S ; E=E°(S(s)/H2Saq) +0,03 log([H+]2/[H2S]) .
E = 0,14 +0,06log[H+] -0,03 log 0,1 =0,14 -0,06 pH+0,03 = 0,17 -0,06 pH.
S(s) +2e-+H+ = HS- ; E1=E°(S(s)/HS-aq) +0,03 log([H+] / [HS-]).
Or Ka1 = [HS-][H+] / [H2S].
E=E°(S(s)/H2Saq) +0,03 log([H+]2/[H2S]) = 0,14 +0,03 log (Ka1[H+] / [HS-]).
E = 0,14 +0,03 log 10-7 +0,03 log([H+] / [HS-]) .
E1 = -0,07 -0,03 pH -0,03 log 0,1 = -0,04 -0,03 pH.
Définir quels sont les domaines de corrosion, passivation et immunité. Les mettre en évidence sur le diagramme.
Domaine de passivation : le métal est oxydé au début puis protégé par une couche d'oxyde.
Domaine de corrosion : l'oxydation du métal est possible.
Domaine d'immunité : toute oxydation du métal est thermodynamiquement impossible.
|
| .
. |
|
|
Construire sur le même graphique la droite frontière entre les espèces O2(g) et H2O et la droite frontière entre les espèces H2O et H2(g). Justifier.
2H2O = O2(g) +e-+4H+ ; E = E°(O2(g) /H2O) +0,06/4 log (PO2 [H+]4) avec PO2 = 1 bar.
E = 1,26 +0,06 log[H+] = 1,26-0,06 pH.
2H2O + 2e- = H2(g) +2HO-. E = E°(H2O /H2(g)+0,03 log (1/(PH2[HO-]2)) avec PH2 = 1 bar.
E = E°(H2O /H2(g) -0,06 log[HO-] = E°(H2O /H2(g)-0,06 log 10-14 +0,06 log [H+] =-0,06 pH.
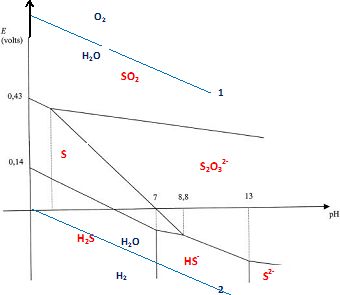
Qu'appelle t-on domaine de stabilité thermodynamique de l'eau ?
Le domaine compris entre les droites
bleues 1 et 2 est le domaine de stabilité de l'eau. Au dessus de la
droite 1, l'eau peut être oxydée en O2(g) ; en dessous de la droite 2 l'eau peut être réduite en H2(g).
Quelles
sont les réactions possibles lorsqu'on place du soufre solide dans une
solution aqueuse ne contenant pas d'autres espèces que l'hydrogène au
nombre d'oxydation +1 et dont on fait varier le pH de 0 à 14 ?
Le soufre et le dihydrogène appartiennent à des domaines distincts : le soufre est réduit.
pH < 7 : S(s) + H2--> H2S.
7 < pH < 8,8 : S(s) + H2+ HO- --> HS- + H2O.
Que se passe t-il si l'eau est aéré ? Donner les équations de réaction.
Le soufre est oxydé par le dioxygène dissout.
1 < pH < 8,8 : 2S(s) + H2O+ O2 --> S2O32-+2H+.
pH<1 : S +O2 --->SO2. |
.
|
|
Grillage de la blende.
La blende est un cristal constitué d'ions zinc et d'ion sulfure.
La préparation du zinc métallique à partir de la blende se fait en deux
étapes. la première sert àpréparer l'oxyde de zinc ( grillage ) ZnO et
la seconde à réduire cet oxyde par le monoxyde de carbone. La réaction
de grillage est à 298 K.
ZnS ( blende) + 1,5 O2(g) --> ZnO(s) + SO2(g).
Montrer qu'il s'agit d'une réaction d'oxydoréduction.
Le nombre d'oxydation du soufre passe de -II dans la blende à +IV dans SO2 ; le nombre d'oxydation de l'élément oxygène passe de 0 dans O2 à -II dans SO2 et dans ZnO.
Calculer l'enthalpie standard, l'entropie standard et l'enthalpie libre standard de réction à 298 K..
DrH=DfH(ZnO(s) +DfH(SO2(g) )-DfH(ZnS(s) )+1,5 DfH(O2(g)).
DrH= -350,5 -296,8 +206,0 = -441,3 kJ / mol.
DrS=S(ZnO(s) +S(SO2(g) )-S(ZnS(s) )+1,5 S(O2(g)).
DrS=43,5 +248,1-57,7-1,5*205 =-73,6 J mol-1 K-1.
DrG=DrH-TDrS= -441,3 103 -298*(-73,6) =-4,19 105 J mol-1.
Quelle sera l'influence sur cette réaction lorsque l'équilibre est atteint :
D'une élévation de température à pression constante ?
La réaction étant exothermique ( DrH< 0), une élévation de température à pression constante déplace l'équilibre dans le sens indirect.
D'une augmentation de la pression totale à température constante ?
Le
nombre total de moles d'espèces gazeuses diminue : une augmentation de
pression à température constante déplace l'équilibre vers la droite (
sens direct ).
D'un ajout isochore et isotherme de dioxygène ?
Cela revient à augmenter la pression à température constante :déplacement de l'équilibre dans le sens direct.
Exprimer K de l'équation en fonction des paramètres suivants : quantités de matière à l'équilibre n(O2), n(SO2), la pression standard P0, la pression totale P et le nombre totalde moles de gaz n.
| Avancement (mol) | ZnS(s) | +1,5 O2 (g) | =ZnO(s) | + SO2(g) | | initial | 0 | A | n0 | 0 | 0 | | à l'équilibre | x | A-x | n(O2) =n0-1,5x | x | n(SO2)=x |
|
| 4-1,5 x |
| x |
n =n0-0,5 x = n(O2)+1,5 x -0,5 x =n(O2) +n(SO2).
Fractions molaires : n(02) / n et n(SO2) / n ; pressions partielles : PO2 = n(02) / n P ; PSO2 = n(SO2) / n P.
K = PSO2 P0½ / P1,5O2 =n(S02) n½ P0½ / (n(02)1,5 P½).
Calculer
l'avancement de la réaction lorsque la réaction est réalisée dans des
proportions stoechiométriques à 298 K et à 1 bar, en partant de 4
moles de O2.
DrG= -RT ln K ; ln K = 4,19 105 /(8,314*298) =169,26 ; K ~ 3,24 1073 ; n = 4-0,5 x ; PO2 =(4-1,5x) / (4-0,5x) ; PSO2 =x / (4-0,5x).
K = x (4-0,5x)½./ (4-1,5x)1,5 ; élever au carré : (4-1,5x)3 =x2 (4-0,5x) / K2.
K est très grand, le second membre est proche de zéro et x~4 / 1,5 ~2,67 mol.
.
|
|
|
Préparation du sulfate d'ammonium.
Le
sulfate d'ammonium est obtenu par neutralisation de l'acide sulfurique
par l'ammoniac en milieu aqueux. La réaction est très exothermique et
se fait sous pression atmosphérique.
2NH3 +H2SO4 --> (NH4)2SO4 ; DH = -456 kJ / mol.
La solution d'acide sulfurique de titre massique 40,3 % est introduite en continu par pompe à un débit de 10 000 kg h-1 dans le réacteuur cylindro-conique. L'ammoniac gazeux est à 20°C et arrive par un tube plongeant au fond du réacteur.
Déterminer
le débit massique d'ammoniac nécessaire si les rapports
stoechiométriques sont respectés, ainsi que le débit massique de
sulfate d'ammonium formé.
Débit massique d'acide sulfurique pur : 10 000 *0,403 =4030 kg h-1.
Quantité de matière correspondante : n = 4030 103 / M(H2SO4) =4030 103 / 98 = 4,1122 104 ~4,11 104 mol h-1.
Quantité de matière d'ammoniac :2n= 2*4,11 104 = 8,224 104 mol h-1.
Débit massique d'ammoniac : 8,224 104 *M(NH3) ~8,224 104 *17 ~1,4 106 g h-1 ~1,4 103 kg h-1.
Quantité de matière de sulfate d'ammonium : n= 4,11 104 mol h-1.
Débit massique de sulfate d'ammonium : 4,11 104 *M(sulfate d'ammonium) =4,11 104 *132 ~5,4 106 g h-1 ~5,4 103 kg h-1.
On
considère que le débit d'ammoniac est de 1400 kg / h et le débit
d'acide de 10 000 kg / h. Les réactifs arrivent à température ambiante
( 20°C).
Calculer le flux de chaleur F dégagé lors de la formation du sulfate d'ammonium.
DH n = 456 *4,1122 104 = 1,875 107 kJ h-1.
Ce
flux de chaleur dégagé permet l'ébullition dans le réacteur à 105°C et
la solution se concentre par évaporation de 2000 kg / h d'eau.
Déterminer le flux de chaleur excédentaire à éliminer.
Energie gagnée par l'ammoniac en une heure : Q1 = chaleur spécifique moyen ammoniac * débit ammoniac * différence de température.
Q1 =2,2 *1400*(105-20)=2,618 105 kJ h-1.
Energie gagnée par la solution d'acide sulfurique en une heure : Q2= chaleur spécifique moyen de l'acide * débit acide * différence de température.
Q2 = 3,1 *10 000*(105-20)=2,635 106 kJ h-1.
Energie mise en oeuvre lors de l'évaporisation de l'eau en une heure : Q3 = caleur latente de vaporisation de l'eau fois masse d'eau.
Q3 = 2520 *2000 =5,04 106 kJ h-1.
Flux de chaleur excédentaire :1,875 107 -2,618 105 -2,635 106 -5,04 106 ~1,1 107 kJ h-1.
Déterminer le titre massique en sulfate d'ammonium dans le réacteur après cette évaporation. Vérifier qu'il y a cristallisation.
L'eau provient de la solution d'acide sulfurique. Initialement :10 000*0,597 = 5970 kg h-1 ; après évaporation : 3970 kg h-1.
Titre massique en sulfate d'ammonium : 5400 / 3970 = 1,36.
A 105 °C, la solubilité du sulfate d'ammonium est 106 g dans 100 g d'eau. Il y a donc cristallisation.
Calculer le débit massique des cristaux et le rendement de la cristallisation.
Quantité de sulfate d'ammonium dissout à 105°C dans 3970 kg d'eau : 1,06*3970 =4208 kg h-1.
Débit massique des cristaux : 5400-4208 =1192 kg h-1 soit un rendement de : 1192/5400 =0,22 ( 22 %).
A quelle température devrait-on refroidir le mélange pour obtenir un rendement de 45 % ?
Débit massique des cristaux :5400*0,45 =2430 kg h-1soit 5400-2430 =2970 kg de sulfate d'ammonium dissout dans 3970 kg d'eau.
Solubilité : 2970 / 3970 = 0,748 kg dans 1 kg d'eau ( 74,8 g dans 100 g d'eau ). Les tables indiquent une température voisine de 18°C.
Pour essorer le sulfate d'ammonium on utilise une série d'essoreuses en
discontinu, dont le panier est cylindrique ( diamètre 1,8 m, profondeur
40 cm ). Chaque essoreuse peut récupérer par cycle 100 kg de cristaux
dont l'humidité résiduaire peut être considérée comme négligeable. La
porosité du gâteau est : Vvide / Vtotal = 0,6. La masse volumique des cristaux est 1770 kg m-3.
Déterminer le volume apparent du gâteau en fin de cycle et en déduire l'épaisseur du gâteau en forme de couronne.
Volume total des cristaux : masse / masse volumique = 100 / 1770 = 0,0565 m3.
Volume vide : 0,0565*0,6 =0,0339 m3.
Volume du cylindre : pR2 h =3,14 *0,92*0,4 = 1,02 m3.
Volume de la couronne cylindrique des cristaux : p(R2-r2) h =0,0565 ; R2-r2= 0,045 m2 ; r2 =0,765 m2 ; r = 0,875 m ; R-r = 0,025 m = 2,5 cm.
|
|
|