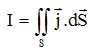Etude d'un câble coaxial. Concours national Deug En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Les vecteurs sont écrits en gras et en bleu. Un câble est constitué de deux armatures métalliques coaxiales ( axe Ox commun ), séparées par un matériau isolant imparfait. - L'armature interne (A1), ou âme, est un conducteur cylindrique plein, de conductivité s et de  rayon r1. - L'armature externe ( A2) est une enveloppe cylindrique pleine, conductrice, de conductivité s et comprise entre deux surfaces cylindriques coaxiales, de rayons r2 et r3 ( avec r2 < r3). - La gaine d'isolant imparfait (G), de conductivité sg, compris entre les surfaces cylindriques de rayons r1 et r2, sépare l'âme de l'armature externe. Loi d'Ohm locale. Les charges mobiles ( électrons de charge -e ) d'un conducteur métallique cylindrique, d'axe Ox orienté par le vecteur unitaire ex, sont animés d'une vitesse v, sous l'action d'un champ électrique uniforme E = Eex appliqué à l'instant t=0 ( avec v(t=0) = 0). Les électrons sont en outre soumis à une force de freinage f = -m/t v, avec t une constante physique positive et m la masse de l'électron. L'action du champ de pesanteur est négligée. Quelles peuvent être les causes de l'existence de la force de freinage ? La force de freinage est due aux collisions des électrons avec les atomes du métal. La vitesse v est colinéaire au vecteur ex. déterminer l’équation différentielle liant le vecteur vitesse au temps t. Relation fondamentale de la dynamique : -eEex+f = mdv/dt. -eEex-m/t v= mdv/dt ; dv/dt +v / t = -eE/m ex. v ' +v / t = -eE/ m. (1) En déduire l'expression vectorielle du vecteur vitesse. Solution générale de l'équation (1) sans second membre : v= A exp(-t / t); A est une constante. Solution particulière de (1), régime permanent : vlim =-eE t / m. Solution générale de (1) : v= A exp(-t / t)-eE t / m. v(t=0) = 0 ; A = eE t / m. v = eE t / m(exp(-t / t)-1). v = eE t / m(exp(-t / t)-1)ex. A.N : e = 1,6 10-19 C ; m = 9,1 10-31 kg ; t =2,5 10-14 s ; E = 0,5 V m-1. || vlim ||= 1,6 10-19 *0,5 *2,5 10-14 /(9,1 10-31)= 0,022 m/s. Comparer v(t=5 t) et vlim.  Conclure sur la durée du régime permanent. v(t=5t) = -vlim(exp(-5)-1) =-vlim (-0,993) ~0,99 vlim. Le régime permanent s'établit très rapidement. Le régime permanent étant établi ; l'égalité v = vlim = µE est établie( µ : mobilité algébrique constante des électrons). j est le vecteur densité de courant électrique et N* est la densité particulaire des électrons ( nombre d'électrons par unité de volume) dans le métal. Montrer que le conducteur métallique satisfait à la loi d'Ohm locale j = sE avec s conductivité électrique du milieu. j = r v avec r =- N*e, densité volumique de charge ; j = - N*e v  = - N*e vlim. j = N*e µE = N*e2t/m E ; s = N*e2t/m. A.N : N* = 6,0 1028 m-3. s =6,0 1028 *(1,6 10-19)2*2,5 10-14 /(9,1 10-31)=4,2 107 W-1 m-1. . . Résistance dun conducteur cylindrique. Un conducteur cylindrique d'axe Ox, de section S constante, est parcouru par un courant d'intensité I constante, et obéit à la loi d'Ohm locale. Le régime est permanent : les vecteurs j et E sont uniformes, et le phénomène de transport est unidirectionnel. La section ( disque ) d'abscisse x=0 est maintenue au potentiel V0 constant. Soit V(x) le potentiel de la section d'abscisse x. Rappeler la relation entre I et j. Le champ électrique dérive du potentiel V ( E = -grad V ). Ecrire l'équation qui relie j à dV(x)/dx. j = s E = - s grad V = -s dV(x)/dx ex. Exprimer en fonction de V0, I, s, S et x le potentiel V(x). I = -s S dV(x)/dx ; puis intégrer : I x = -s S (V(x)-V0) ; V(x) =V0-Ix / (s S). En déduire la résistance électrique R(x) du conducteur cylindrique compris entre les abscisses x=0 et x. R(x) = (V(x)-V0) / I =x / (s S). Les propriétés et résultats précédents sont applicables aux armatures (A1) et (A2) du câble coaxial. Exprimer en fonction de s et r1 la résistance linéique l1 du conducteur (A1). l1 = 1/(pr21s). Exprimer en fonction de s, r2 et r3 la résistance linéique l1 du conducteur (A2). l2 = 1/(p(r23 -r22 )s). . Résistance de la gaine d'isolant imparfait. Les armatures (A1) et (A2) sont considérées, uniquement dans ce paragraphe, comme  des conducteurs parfaits portés aux potentiels respectifs V1 et V2 ( avec V1 > V2) uniformes et constants. La gaine d'isolant homogène (G) comprise entre les armatures se comporte comme un conducteur ohmique de faible conductivité sg. Il est parcouru par un courant électrique de fuite If. Le phénomène est à symétrie cylindrique et les effets de bords sont négligés : les lignes de courant dans l'isolant sont radiales ( donc orthogonales à l'axe Ox) sur toute la longueur l du câble et le vecteur densité de courant ne dépend que du rayon r. Ecrire l'équation qui lie la densité de courant j(r) à la dérivée dV(r)/dr. j(r) = sg E = - sg grad V = -sg dV(r)/dr er. On choisit une surface cylindrique d'axe Ox, de longueur l et de rayon r ( r1 < r < r2). Relier l'intensité If à la densité de courant. If = -sg 2prl dV(r)/dr. Déterminer la résistance R de la gaine d'isolant de longueur l. dV(r) = If / (-sg 2pl ) dr /r ; intégrer de (1) à (2) : V2-V1 = If / (-sg 2pl ) ln(r2/r1) ; R =(V1-V2) / If ; R= ln(r2/r1) /(sg 2pl ). Etude du câble coaxial. Les armatures ont la conductivité s. Dans le plan d'abscisse x=0, la section de l'armature interne est maintenue au potentiel V1(0) = V1 constant et la section de l'armature externe est maintenue au potentiel V2(0) = V2 constant avec V1 > V2. Dans le plan d'abscisse x, la section de l'armature (A1) se trouve au potentiel V1(x) et la section de l'armature (A2) présente le potentiel V2(x). 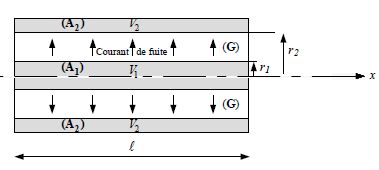Par ailleurs, toujours dans le plan d'abscisse x, ces sections sont traversées par des courants ( lignes de courant parallèles à Ox , de même intensité i(x), mais de sens opposés. Soit i(0) = i0, l'intensité constante du courant dans (A1) et (A2), à l'abscisse x=0. 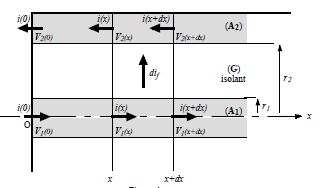La tranche élémentaire de câble coaxial, comprise dans les plans d'abscisse x et x+dx, est partiellement symbolysée par : Exprimer le courant de fuite élémentaire dif dans la tranche d'épaisseur dx. i(x) = dif + i(x+dx) ; dif = i(x+dx) -i(x). Etablir une équation différentielle liant V1(x) et i(x), pour l'armature (A1) de résistance linéiue l1. Même question pour l'autre armature ainsi que pour l'isolant. Loi d'ohm dans la tranche élémentaire : V1(x) -V1(x+dx) =l1 i(x) dx ; dV1/dx = -l1 i(x). V2(x) -V2(x+dx) = -l2 i(x) dx ; dV2/dx = +l2 i(x). V1(x)-V2(x) = R l dif /dx. dif = i(x+dx) -i(x) = -di ; V1(x)-V2(x) = -R l di/dx.(2) On pose lg =R l et w2 =(l1 +l2) / lg ; écrire une équation différentielle du second ordre en i(x). Dériver (2) par rapport à x : dV1/dx -dV2/dx =-R l d2i/dx2. -l1 i(x)-l2 i(x)= - lg d2i/dx2 ; d2i/dx2 -(l1 +l2) / lg i(x) = 0 ; d2i/dx2-w2 i(x)=0. Le câble est supposé de longueur infinie. L'intégration de l'équation différentielle précédente conduit à : i(x) = I1 exp(-wx) + I2 exp(wx) avec I1 et I2 des constantes d'intégration. Déterminer I1 et I2. i(0) = i0 = I1 + I2 ;si I2 diffère de zéro, i(x) tend vers l'infini, ce qui n'est pas physiquement possible : donc I2 = 0. i(x) = i0 exp(-wx).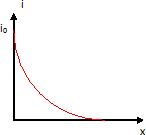 La résistance de ce câble coaxial est définie par Rc = (V1(0)-V2(0))/ i(0). Etablir les expressions de V1(x) et V2(x). dV1 = -l1 i(x) dx = -l1i0 exp(-wx)dx ; par intégration : V1(x) = l1i0 /w exp(-wx)+ constante. V1(0) =V1= l1i0 /w + constante ; constante = V1 - l1i0 /w ; V1(x) =V1+ l1i0 /w (exp(-wx)-1). dV2 = l2 i(x) dx = l2i0 exp(-wx)dx ; par intégration : V2(x) = -l2i0 /w exp(-wx)+ constante. V2(0) =V2= -l2i0 /w + constante ; constante = V2 + l2i0 /w ; V2(x) =V2- l2i0 /w (exp(-wx)-1). Dessiner l'allure de la courbe v(x) = V1(x) -V2(x). v(x) =-lg di/dx = lg i0 w exp(-wx).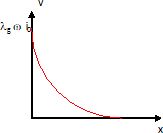 Exprimer Rc en fonction de l1, l2 et lg. Rc = v(x) /i(x)=lg w =( lg(l1 +l2))½. Modélisation simple du câble. Le câble peut être modélisé par un circuit A1A2, constitué d'une chaîne de n modules identiques comportant chacun trois résistors. Un dipôle résistor X1X2 de résistance 2R, est branché en parallèle à l'extrémité de la chaîne. 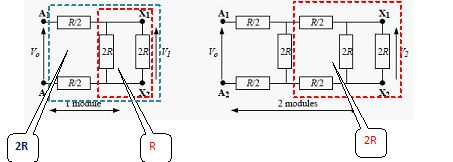Le dipôle A1A2 est équivalent à un résistor. Exprimer, en fonction de R, la résistance équivalente R1 dans le cas d'une chaîne comportant un seul module. Deux résistances identiques de valeur 2R sont en dérivation : résistance équivalente R. Trois résistances de valeur, ½R, ½R, R sont en série : R1 = ½R+½R+R = 2R. Même question pour une chaîne à 2 modules, puis à n modules. La résistance équivalente du second module vaut 2R. Deux résistances identiques de valeur 2R sont en dérivation : résistance équivalente R. TRois résistances de valeur, ½R, ½R, R sont en série : R2 = ½R+½R+R = 2R. Chaîne à n modules : hypothèse Rn = 2R. Calculons Rn+1 : Deux résistances identiques de valeur 2R sont en dérivation : résistance équivalente R. Trois résistances de valeur, ½R, ½R, R sont en série : Rn+1 = ½R+½R+R = 2R. Le dipôle A1A2 est alimenté par un générateur de tension constante V0 = VA1-VA2. Déterminer en fonction de V0,et R, la tension V1 =VX1-VX2 aux bornes du résistor X1X2 dans le cas d'une chaîne à 1 module. I = V0 / R1 = V0/(2R) ; V1 = R I = ½V0. Même question pour une chaîne à 2 modules puis à n modules. I = V0 / (2R) ; V1 =½V0 ; V2 =½V1 = V0/4 = V0 / 22. Chaîne à n modules : hypothèse Vn = V0/2n. Calculons Vn+1 : Vn+1 =Vn / 2 = ½ V0/2n = V0 / 2n+1. En déduire la valeur de Vinfini pour une chaîne de longueur infinie. Vinfini tend vers zéro si n tend vers l'infini. .

menu