Mouvement hélicoïdal. Concours national Deug En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Les vecteurs sont écrits en gras et en bleu. Le référentiel R, considéré comme galiléen, est rapporté au repère (O, x , y , z ). Un mobile P, de masse m , considéré comme ponctuel, est lâché avec une vitesse initiale v0 d’une hauteur z0. Il est astreint à glisser sans frottement sur une hélice d’équations : x = Rcos q ; y = R sin q ; z = hq où R et h sont respectivement le rayon et le pas apparent de l’hélice. 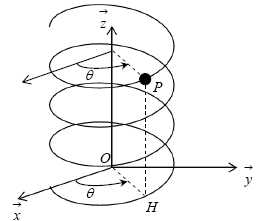La position du mobile P est repérée grâce à l’angle q défini dans le plan xOy où H est la projection orthogonale de P dans ce plan.  Exprimer dans R la vitesse vP du mobile P. On considère la base locale cylindrique. 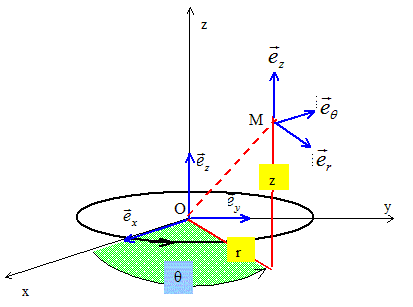OM = (r2 +z2)½ = (x2 +y2 +z2)½ =(R2 +(hq)2)½. r = R er +hq ez. v =R q' eq + hq'ez. Exprimer dans R l’accélération a du mobile P. a= -Rq'2er +R q'' eq+ hq''ez. Réaliser le bilan des actions mécaniques extérieures appliquées au mobile P. Le mobile est soumis à son poids P et à la force de liaison F entre le solide et l'hélice. Énoncer le principe fondamental de la dynamique appliqué au mobile P. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées au système est égale au produit de la masse du système par l'accélération de son centre d'inertie. . . En déduire l'équation du mouvement. Déterminer la loi d'évolution q(t) en fonction du temps t, v0 et z0. T = v(P) / ||v|| : vecteur directeur de la tangente en M à la courbe. (en supposant v(P) non nul)  ||v||= q' (R2 +h2)½ = A q' ; T  = R /A eq + h / Aez. Ce vecteur T est constant dans la base cylindrique. On calcule les produits scalaires suivants : a .T = R2/A q''+h2/A q''=(R2+h2)/A q''=A q''. P . T =  -mgh / A. F.T = 0 car F est normale à la trajectoire. ma = P + F ; m a .T =P . T +F.T : mA q''=-mgh / A ; q''=-gh /A2 = -gh /(R2+h2) = -C = constante. Intégrer : q' = Ct + B, avec B une constante ; q = ½Ct2 + Bt + C, avec C une constante ; A t = 0, q0 = C =z0/h ; q'0=B avec q'0=v0/A ; q = -½gh /(R2+h2)t2+v0/R2+h2)½t +z0/h. . En déduire les composantes de la force de liaison entre le mobile P et l'hélice. Suivant er : Fr =-mRq'2 ; q' = Ct + B =q' = -gh /(R2+h2)t + v0/R2+h2)½. Suivant eq : Fq =mR q'' ;  q'' = -gh /(R2+h2) Suivant ez : Fz -mg=mh q''. Fz =m(g+h q''). .

menu