Mathématiques.
Concours Aspts Lille 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
1. Effectuer le
calcul suivant. Donner la réponse sous la forme d'une fraction
irréductible.
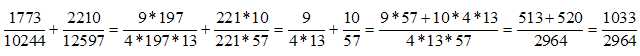
2. Un philatéliste
possède 1631
timbres français et 932 timbres étrangers. Il souhaite vendre toute sa
collection en réalisant des lots identiques, c'est à dire comportant le
même nombre de timbre et la même répartition de timbres français et
étrangers. Calculer le nombre maximal de lots qu'il pourra constituer.
1631 =7*233 ; 932 =4*233.
Il peut constituer 233
lots contenant chacun 7
timbres français et 4 timbres étrangers.
3.
Deux trains effectuent le trajet Paris Nantes. Un train corail part de
Paris à 14 h et roule à 120 km/h. Un TGV part de Paris à 15 h et roule
à 300 km/h. A quelle distance de Paris le TGV ratrappe-t-il le train
corail ?
Soit x la distance parcourue par chaque train.
x= 120 t ; x = 300(t-1) ; t =x / 120 ; x =300(x / 120 -1).
x =300 / 120 x -300 ; x=2,5 x -300 ; 1,5 x = 300 ; x = 200.
4. Ecrire un système
de deux équations à 2 inconnues pour trouver le rayon des disques et la
largeur du cadre.
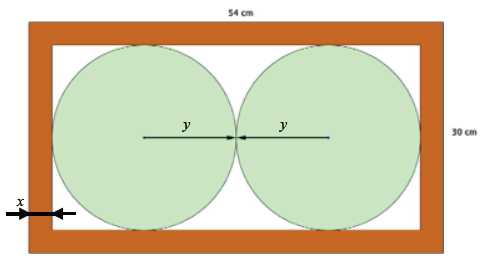
Calculer les dimensions du cadre intérieur de deux manières différentes
:
Longueur du cadre intérieur : 54-2x
= 4y.
Largeur de ce cadre : 30-2x
= 2 y.
27-x=2y ; 27-x=30-2x ; x=3 et y = 12.
5. Quelles
expressions ne sont pas des identités remarquables ?
4x2+2x+1. Ce n'est pas une identité remarquable.
9x2-6x+1 = (3x-1)2.
x2-81 =(x+9)(x-9).
16x2+8x+4.
Ce n'est pas une
identité remarquable.
6. Un bassin est
alimenté par
deux fontaines dont le débit est constant. Si on laisse couler la
première fontaine pendant 4 heures et la seconde pendant 3 heures, la
quantité d'eau recueillie au total est de 55 L. Si on
laisse couler la première fontaine pendant 3 heures et la seconde
pendant 4 heures, la quantité d'eau recueillie au total est de 57 L.
Calculer le débit
de chaque fontaine.
x et y : débits des fontaines en litre par heure.
4x +3y =55 et 3x+4y = 57.
12x + 9y =165 et 12x + 16y =228.
Soustraire : 16y-9y =228-165 ; 7y = 63 ; y = 9 L / h.
Puis 4x+3*9 =55 ; 4x =55-27 = 28 soit x = 7 L/ h.
Sachant
que le bassin peut contenir 320 litres, combien de temps faudra t-il
pour le remplir si les deux fontaines coulent en même temps ?
320 / (9+7) = 20 heures.
|
| .
. |
|
|
7.
Une mouche située en M voit
arriver sur elle une balle de 10 cm de diamètre. Sachant qu'elle se
trouve à une distance MH de 7 cm de cette balle, calculer sous quel
angle elle voit cette balle.
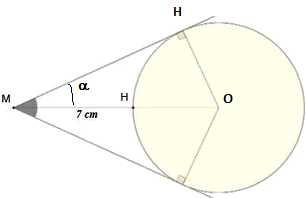
sin a
= OH / OM = 5 / (7+5) =0,417 ; a =
24,6° puis 2*24,6 ~49,2°.
8.
L'unité de longueur est le centimètre. On considère un triangle ABC et
un parallélogramme MNCP. Le but du problème est de trouver AM pour que
le périmètre du parraalélogramme MNCP soit égal à 11. On donne BC =6 ;
AB =8 ; AC=5.
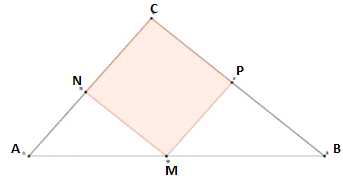
Périmètre du parallélogramme : 2MN + 2NC=11 ; MN+NC = 5,5.
Relation de Thalès :AC / AN = BC / MN = AB / AM.
MN = BC . AM / AB = 6 AM / 8 =0,75 AM.
AN =AC . AM / AB =5 AM /8 =0,625 AM.
NC = AC-AN =5-0,625AM.
0,75 AM +5-0,625 AM = 5,5.
0,125 AM = 0,5 ; AM = 0,5 / 0,125 ; AM=
4.
|
.
|
|
9.
Une machine est réglée afin de fabriquer des allumettes d'une longueur
moyenne de 5 cm. Régulièrement, on doit effectuer un contrôle
statistique pour vérifier si la machine ne s'est pas déréglée. On
considère que la machine est bien réglée si les deux critères suivants
sont respectés :
-Critère de position : la longueur moyenne de l'allumette est comprise
entre 49 mm et 51 mm.
-
Critère de dispersion : au moins 90 % de l'effectif total des
allumettes
a une longueur comprise entre 0,95 L et 1,05 L ( ou L est la
longueur
moyenne d'une allumette).
Voici le relevé
fait lundi mtin :
| Longueur
( mm) |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
| Effectif |
6 |
11 |
15 |
19 |
89 |
101 |
208 |
302 |
200 |
22 |
13 |
9 |
5 |
Calculer L en mm. Le
critère de position est-il respecté ?
Effectif total : N=6+11+15+19+89+101+208+302+200+22+13+9+5=1000
L =(44*6 +45*11 +46*15 +47*19 +48*89 +49*101 +50*208 +51*302
+52*200 +53*22 +54*13 +55*9 +56*5) / 1000 .
L =(264 + 495 + 690 + 893 + 4272 + 4949 + 10400 + 15402 + 10400 +1166 +
702 + 495 +280) / 1000 =50,41. L
~ 50,4 mm. Le critère de position est vérifiée.
Calculer 0,95 L et 1,05 L. En déduire le nombre d'allumettes qui ont
une longueur comprise entre 0,95 L et 1,05 L.
0,95L =0,95*50,41 =47,89 ~ 47,9
mm
1,05 L = 1,05*50,41 =52,93 ~52,9
mm.
Nombre d'allumettes ayant une longueur comprise entre 47,9 mm et 52,9
mm :
89 +101 +208 +302 +200 = 900.
Le critère de dispersion est-il respecté ? La machine est-elle bien
réglée ?
900/100 =0,9 ( 90 %). Le critère de dispersion est respecté. Les deux
critères étant respectés, la machine est bien réglée.
Voici
le relevé fait mardi matin :
| Longueur
( mm) |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
| Effectif |
4 |
26 |
11 |
26 |
103 |
101 |
297 |
302 |
200 |
22 |
13 |
9 |
5 |
Quel critère n'est
pas respecté ? Montrer que la machine n'est pas bien réglée.
Effectif
total : N=4+26+11+26+103+101+297+302+200+22+13+9+5=1119
L =(44*4 +45*26 +46*11 +47*26 +48*103 +49*101 +50*297 +51*302
+52*200 +53*22 +54*13 +55*9 +56*5) / 1119 .
L =(176 + 1170 + 506 + 1222 + 4944 + 4949 + 14850 + 15402 + 10400 +1166
+ 702 + 495 +280) / 1000 =50,28. L
~ 50,3 mm. Le critère de position est vérifiée.
0,95L
=0,95*50,28 =47,8 mm ; 1,05 L =
1,05*50,28 =52,8 mm
Nombre d'allumettes ayant une longueur comprise entre 47,9 mm et 52,9
mm :
103 +101 +297 +302 +200 = 1003.
1003/1119
=0,896 ( 89,6 %). Le critère de dispersion n'est pas respecté. Un seul
critère étant respecté, la machine n'est pas bien réglée.
|
|
|