Comment réduire le
taux d'erreur d'un processus biologique ? Second
concours, école normale supérieure
2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
L'azote dans le
monde vivant.
1. Quel est le pourcentage de chance d’avoir un acide aminé incorrect dans une protéine de 1000 acides aminés ?
Les erreurs de traduction apparaissent à une fréquence de 10-5, c’est à dire qu’un un acide aminé incorrect est incorporé tous les 100 000 acides aminés. ( 10-3 %).
2. Donner l’expression de s en fonction de DDG.
Calculer la fidélité du processus de reconnaissance. Est-ce que cette
valeur permet d’expliquer la fidélité observée expérimentalement lors
de la traduction ?
DDG =DrG°A-DrG°N =RT ( ln KdA-ln KdN) =RT ln ( KdA / KdN) = RT ln (1/s) = -18 103 J mol-1.
ln s =-DDG /(RT)= 18 103 ( Rt) = 18 103 / (8,314*(273+37)=6,98 ; s ~1,1 103.
Non. Cette valeur est 100 fois plus petite que celle observée expérimentalement.
3. Pour l’ARNt X, donner l’expression de d[XC]/dt, en fonction de [X], [XC], [C] et des constantes du problème.
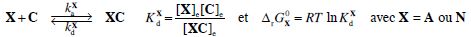
d[XC]/dt = kaX [X][C] -kdC[XC].
4. En déduire l’expression de KdX en fonction des constantes cinétiques du problème.
K dX =kdX / kaX = constante de dissociation du complexe.
K dA =kdA / kaA =
K dA =kdA / ka ;
K dN =kdN / kaN
K dN =kdN / ka.
5. Montrer que le paramètre de sélectivité intrinsèque s peut s’écrire : s =kdN / kdA.
s=
K dN /
K dA = kdN / kdA.
Traduction avec une étape de lecture.
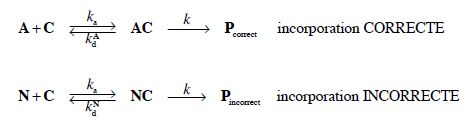
6. On note R1A = d[Pcorrect ] / dt la vitesse d’incorporation d’un acide aminé correct.
Donner l’expression de R1A en fonction de k et [AC].
R1A =k [AC].
7. En appliquant l’approximation des états quasi-stationnaires aux espèces intermédiaires, montrer que l’on peut écrie R1A sous la forme : R1A = α1A[A][C] avec α1A une constante que l’on exprimera en fonction des constantes cinétiques du problème.
d[AC]/dt = 0 = ka[A|[C] -(k+kdA)[AC].
[AC]=ka[A|[C] / (k+kdA).
R1A =kka / (k+kdA)[A|[C] avec α1A =kka / (k+kdA).
8. On note de même R1N = d[Pincorrect ] / dt la vitesse d’incorporation d’un acide aminé incorrect. Par analogie avec les questions 5 et 6, montrer que R1N = α1N[N][C] avec α1N une constante que l’on exprimera en fonction des constantes cinétiques du problème.
d[NC]/dt = 0 = ka[N|[C] -(k+kdN)[NC].
[NC]=ka[N|[C] / (k+kdN).
R1N =k [NC]=kka / (k+kdN)[N|[C] avec α1N =kka / (k+kdN).
9. On définit la fidélité A1 du processus de traduction par : A1 = α1A /α1N
avec A1 compris entre 1 et A1max.
On considère maintenant k comme une variable. Donner l’expression de A1 = A1(k) en faisant apparaître les paramètres intrinsèques kdA et kdN .
A1 =(k+kdN) / (k+kdA).
10. Donner l’expression de la fidélité maximale A1max . Quelle condition sur k doit on avoir pour atteindre A1max ? Commenter.
11. Montrer que : A1max = s n avec n un entier que l’on précisera.A1max = kdN / kdA = s.k doit être petit devant kdA et devant kdN.
k << kdN : l'incorporation incorrecte se produit le moins souvent possible.
k << kaN :AC se dissocie en conduisant peu à Pcorrect.
12. En déduire une estimation de A1max . Commenter cette valeur par rapport à la fidélité maximale observée expérimentalement.
A1max=s ~1,1103.
Cette valeur est 100 fois plus petite que celle observée expérimentalement.
|
| .
. |
|
|
Traduction avec une étape de lecture suivie d’une étape de relecture.
Au processus de lecture que l’on vient d’étudier s’ajoute également un processus de relecture.
En réalité, après son appariement avec C, A subit une modification chimique : A s’apparie à
C puis est convertit en A*. Cette réaction est irréversible. L’ARNt modifié A* peut soit se
dissocier du codon, soit donner son acide aminé à la chaine peptidique naissante. On peut
résumer ce processus par le système d’équations suivant :
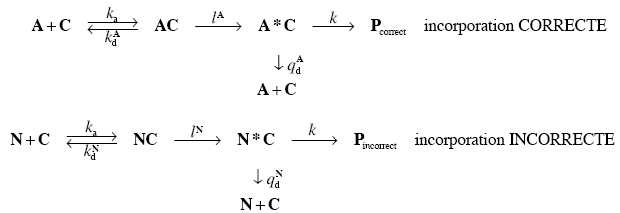 13. On note R2A = d[Pcorrect ]/ dt la vitesse d’incorporation d’un acide aminé correct.
Donner l’expression de R2A en fonction de k et [A*C].
R2A =k[A*C].
14. En appliquant l’approximation des états quasi-stationnaires aux espèces intermédiaires, montrer que l’on peut écrie R2A sous la forme : R2A = a2A[A][C] avec a2A une constante que l’on exprimera en fonction des constantes cinétiques du problème.
d[AC]/dt=0 =ka[A|[C] -(kdA+lA)[AC] ; [AC] = ka[A|[C] /(kdA+lA).
d[A*C]/dt = 0 = lA[AC]-(k+qdA)[A*C] = lAka[A|[C] /(kdA+lA)-(k+qdA)[A*C].
[A*C] = lAka[A|[C] /((kdA+lA)(k+qdA)).
R2A =kka lA / ((kdA+lA)(k+qdA)) [A|[C] avec α2A =kka lA / ((kdA+lA)(k+qdA)).
15. On note de même R2N = d[Pincorrect ]/ dt la vitesse d’incorporation d’un acide aminé incorrect. Par analogie avec les questions 11 et 12, montrer que R2N = a2N[N][C] avec a2N une constante que l’on exprimera en fonction des constantes cinétiques du problème.
d[NC]/dt=0 =ka[N|[C] -(kdN+lN)[NC] ; [AC] = ka[N|[C] /(kdN+lN).
d[N*C]/dt = 0 = lN[NC]-(k+qdN)[N*C] = lNka[N|[C] /(kdN+lN)-(k+qdN)[N*C].
[N*C] = lNka[N|[C] /((kdN+lN)(k+qdN)).
R2N =kka lN / ((kdN+lN)(k+qdN)) [N|[C] avec α2N =kka lN / ((kdN+lN)(k+qdN)).
|
|
|
|
16. On définit la fidélité A2 du processus de traduction par : A2 = α2A / α2N compris entre 1 et A2max.
On considère maintenant k et l comme des variables. Donner l’expression de A2 = A2(k, l) en faisant apparaître les paramètres intrinsèques kdA , kdN , qdA et qdN .
A2 = lA (kdN+lN)(k+qdN) / ((kdA+lA)(k+qdA)lN) = (kdN+l)(k+qdN) / ((kdA+l)(k+qdA)).
17. Donner l’expression de la fidélité maximale A2max en fonction de kdA , kdN , qdA et qdN .
Quelles conditions doivent remplir k et l pour atteindre la fidélité maximale A2max ? Commenter.
l=0 ; k=0 : A2max = kdN/ kdA qdN / qdA.
k doit être petit devant qdA et devant qdN ; l doit être petit devant kdA et devant kdN ;
k << qdN : l'incorporation incorrecte se produit le moins souvent possible.
k << qaN : A*C se dissocie en conduisant peu à Pcorrect.
18.
Etant donné que la dissociation des complexes XC et X*C (X = A ou N)
fait intervenir la même interaction anticodon-codon, on peut faire
l’approximation kdX = qdX .
Montrer que : A2max = sn avec n un entier que l’on précisera. En déduire une estimation de la fidélité maximale A2max que l’on peut atteindre dans ces conditions. Commenter cette valeur par rapport à la fidélité observée expérimentalement.
A2max = (kdN/ kdA )2 = s2~ 106, valeur beaucoup plus proche de la valeur expérimentale.
19. On définit les paramètres de répartition i = kdA / l et f = qdA / k . Exprimer A2 = A2(i, f) en faisant apparaitre le paramètre de sélectivité intrinsèque s.
20. On fait l’approximation i = f. Montrer que A2 = A2(i) = ((1+si) / (1+i))2.
A2=(kdN/ l+1)(1+qdN/k) / ((kdA/ l +1)(1+qdA/k)).
A2 =(s kdA/ l+1)(1+s qdA/k) / ((i +1)(1+f)) = (s i +1)(1+s f) / ((i +1)(1+f))= ((1+si) / (1+i))2.
21.
En prenant en compte les approximations des questions 17 et 19, déduire
que l’on peut écrire la constante de vitesse de formation de la liaison
peptidique a2A=ka[(s-A2½) / (s-1)]2.
i=f donne : l =k kdA /qdA ; kdA / l = qdA / k.
A2 ½=(1+si) / (1+i) =(1+s kdA / l ) / (1+kdA / l) = (1+s qdA / k ) / (1+qdA / k) = (1+s kdA / k ) / (1+kdA / k).
A2 ½ =( k+s kdA) / (k+kdA) ; s-A2 ½ = [s (k+kdA)-( k+s kdA)] / (k+kdA) =k(s-1) /(k+kdA).
k / (k+kdA) = (s-A2½) / (s-1).
α2A =kka l / ((kdA+ l )(k+qdA)) = k2ka kdA /qdA / ((kdA+ k kdA /qdA )(k+qdA)).
α2A =k2ka /(kdA+ k )2= ka [ k /(kdA+ k ) ]2 = ka [(s-A2½) / (s-1)]2.
22. Quelle est la valeur maximale de la constante de formation de la liaison peptidique α2A (A2) ?
Pour quelle valeur de fidélité A2 obtient-on la valeur maximum de α2A (A2) ? Interpréter.
α2A (A2)max = ka = 108 M-1 s-1 pour la valeur minimale de A2=1.
23. Donner une estimation de la constante de formation de la liaison peptidique α2A en utilisant la fidélité observée expérimentalement. Comparer cette valeur avec la valeur maximale de α2A . Commenter la perte de vitesse associée au gain de fidélité.
La fidélité de traduction des protéines est 105.
α2A (A2) = 108[(s-102,5) / (s-1)]2=108[(s-316) / (s-1)]2=108[(1,1 103-316) / (1,1 103-1)]2~ 5 107.
24.
Proposer un moyen d’augmenter la fidélité de la traduction sans
modifier la vitesse de la réaction de formation de la liaison
peptidique.
|
|
|
|