Déplacement et déformation d'un objet biologique viscoélastique. Second concours, école normale supérieure 2012

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.


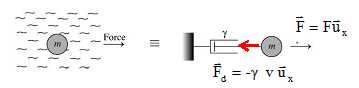
Modèle simple du déplacement d'un objet biologique.
Une protéine ou une cellule se déplaçant à la vitesse v dans un liquide visqueux subit une force de frottement fluide due à la viscosité du milieu qui varie linéairement avec la vitesse. On peut modéliser un tel système par un objet ponctuel de masse m accroché à un piston de constante de frottement g. La force exercée par le piston sur l’objet modélise la force de frottement fluide Fd que subit l’objet lors de son déplacement dans le liquide visqueux.
Les protéines et les cellules étant des objets très petits les forces gravitationnelles sont négligeables.
On suppose qu’initialement l’objet de masse m est immobile et qu’à l’instant t = 0 une
force constante F est appliquée conduisant au déplacement de l’objet à la vitesse v.

1. Pour une sphère de rayon r se déplaçant dans un liquide de viscosité h, la constante
de frottement est g = 6phr . Donner une estimation de la force de frottement agissant sur une protéine sphérique de diamètre 6 nm se déplaçant dans l’eau à la vitesse de 8 m/s. La viscosité de l’eau h = 10–3 Pa.s–1.
Fd = 6phrv =6*3,14 *10-3*3 10-9 *8 =4,5 10-10 N.
2. Comparer cette valeur avec celle du poids d’une protéine de 100 kDa soumis au champ gravitationnel terrestre. Commenter l’approximation qui néglige les forces gravitationnelles.
On caractérise la taille des protéines par leur masse molaire exprimée en dalton (Da). 1 Da = 1
g/mol.
m = 100 / 6 1023 =1,7 10-22 g = 1,7 10-25 kg ; poids = mg = 1,7 10-25 *9,8 ~1,7 10-24 N.
La force de frottement fluide est très supérieure au poids de la protéine. Ce dernier peut être négligé.
 3. Faire le bilan des forces s’appliquant sur l’objet ponctuel de masse m.
La force de frottement fluide et  la force constante responsable du déplacement de l'objet s'appliquent sur la protéine.
4. En déduire l’équation différentielle du mouvement vérifiée par v.
Ecrire la seconde loi de Newton sur un axe horizontal orienté à droite.
mdv / dt = F -g v ; dv / dt + g / m v = F / m. (1)
5. Quelle est la vitesse stationnaire terminale v(oo) de l’objet ?
dv(oo) / dt = 0 ; v(oo) = F / g.
6. Montrer que l’évolution temporelle de v la vitesse de l’objet est décrite par l’équation suivante avec la constante de temps t que l’on écrira en fonction des constantes du problème.
Solution générale de dv / dt + g / m v =0 : v = A exp(- g / m t) avec A une constante.
Solution particulière de (1) : v = v(oo).
Solution générale de (1) : v = A exp(- g / m t) + v(oo).
v(t=0) =0 ; A = - v(oo).
v = v(oo) (1-exp(- g / m t) ) ; on pose t = m / g.
7. Dessiner l’allure de l’évolution temporelle de v.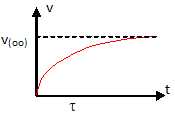
8. Une bactérie telle que E. coli utilise des moteurs moléculaires actionnant des flagelles pour se déplacer. Ces moteurs permettent à une bactérie de se déplacer à environ 25 μm/s. Quelle est la force que doit générer ces moteurs pour pouvoir déplacer une bactérie, sachant que dans le cas d’une bactérie la constante de frottement g est 20 nN.s/m ?
F = g v(oo) = 20 10-9 *25 10-6 =5,0 10-13 N.
.
.




On considère maintenant une bactérie se déplaçant à la vitesse initiale v(0) = 25 μm/s suivant
l’axe des x et dont les moteurs s’arrêtent brutalement à l’instant t = 0.
9. Écrire l’équation différentielle du mouvement vérifiée par v dans ce cas.
La bactérie est soumise uniquement à la force de frottement fluide. Sur l'axe des x, la seconde loi de newton s'écrit : mdv / dt = - g v ; dv / dt + g / mv =0.
10. En déduire l’expression de v(t) en fonction de la vitesse initiale v(0), et des constantes du problème.
v = B exp (-g/m t ) avec B une constante.
A l'instant initial, v = v(0) ; v = v(0)exp (-g/m t ).
11. Dessiner l’allure de l’évolution temporelle de la vitesse v dans ce cas.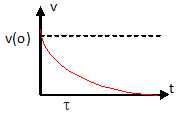
12. Montrer que la distance parcourue par la bactérie avant de s’arrêter peut s’écrire sous la forme x = v(0) t.
L'abscisse x est une primitive de la vitesse : x =v(0) (-m /g ) exp (-g/m t )+ Cste.
L'instant initial est choisit comme origine des abscisses :
0 =v(0) (-m /g )  +Cste ; x = v(0) (-m /g ) exp (-g/m t )+v(0) m /g .
x =v(0) m /g (1-exp (-g/m t )).
Au bout d'un temps très long, la bactérie est à l'arrêt ;
 la distance parcourue est : v(0) m /g  = v(0) t.
13. Calculer la distance parcourue par une bactérie sphérique de 1 μm de rayon et de densité r = 1000 kg/m3 une fois que ces moteurs s’arrêtent. On prendra de nouveau 20 nN.s/m pour le coefficient de frottement de la bactérie dans l’eau. Commenter cette valeur par rapport à une taille caractéristique que vous jugerez pertinente.
Volume de la sphère V= 4 /3 p r3 = 4 / 3*3,14 *10-18 =4,2 10-18 m3.
Masse de la bactérie : m = r V = 1000 *4,2 10-18 = 4,2 10-15 kg.
Distance parcourue : 25 10-6 *4,2 10-15 / (20 10-9)=5,3 10-12 m.
Cette distance est très inférieure à la taille d'une bactérie ( quelques microns). L'arrêt est quasiment instantané, dès que les moteurs ne fonctionnent plus..









Modèle simple de la déformation d’un objet biologique viscoélastique.
Une protéine est un objet flexible (ou viscoélastique) capable d’adopter différentes conformations. Une protéine qui subit un changement conformationel important dans un liquide dû à une force F peut être modélisée par un objet ponctuel de masse m (symbolisé par le point sur le schéma ci-dessous) relié à un ressort de constante de raideur k en parallèle avec un piston de constante de frottement g. Le ressort modélise la raideur de la protéine et le piston les forces de frottement fluide. On considère dans cette partie que la masse de la protéine m est nulle (m = 0).
Le ressort est au repos à l’instant t = 0. On applique une force constante F conduisant à l’élongation x.
14. Rappeler l’expression de la force exercée par le ressort sur l’objet ponctuel.
15. Faire le bilan des forces s’appliquant sur la masse m. En déduire l’équation différentielle vérifiée par x.

Projection de la seconde loi de Newton sur l'axe des abscisses :
F -kx -g dx/dt = 0 ; dx/dt  +k / g x = F / g. (2).
16. Quelle est la longueur d’élongation x(oo) à l’état stationnaire ?
dx(oo)/dt =0 ; x(oo) = F / k.
17. Montrer que l’élongation du ressort dans ce cas est décrit par l’équation suivante avec la constante de temps t' exprimée en fonction des constantes du problème.
Solution générale de  dx/dt  +k / g x = : x = A exp(-k / g t) avec A une constante.
Solution particulière de (2) : x(oo) = F / k.
Solution générale de (2) : x = A exp(-k / g t) + x(oo).
x(t=0) =0 ; A = - x(oo).
x = x(oo) (1-exp(-k / g t) ) ; on pose t' = g / k.
18. Dessiner l’allure de l’évolution temporelle de x.
On suppose maintenant que la protéine est maintenue dans une conformation étirée par une contrainte, par exemple, un « crochet interne ». Un modèle mécanique pour cet arrangement est un ressort en parallèle avec un piston et un crochet. Supposons maintenant que la contrainte est soudainement relâchée.
19. Ecrire l’expression de x(t). On fera apparaître l’élongation initiale x(0) et la constante t’.
x =(x(0)-x(oo) )exp(-k / g t) +x(oo) ; on pose t' = g / k.
20. La constante t’ est appelé temps de relaxation et donne l’ordre de grandeur de la durée nécessaire à la protéine pour atteindre sa conformation d’équilibre. Sachant que pour une protéine globulaire de 100 kDa, la constante de frottement g vaut 60 pN.s/m et que l’élément élastique à une raideur k de 4 pN/nm, estimer le temps nécessaire à la protéine pour relaxer dans son état de repos.
t' = g / k= 60 10-12 / (4 10-3) =1,5 10-8 s.
Modèle complet de la déformation d’un objet biologique viscoélastique.
On considère maintenant le cas décrit dans la partie précédente mais cette fois-ci sans négliger la masse de la protéine. Une protéine est modélisée par un objet ponctuel de masse m relié à un ressort de constante de raideur k = 4 pN/nm en parallèle avec un piston de constante de frottement g = 60 pN.s/m. À l’instant t = 0, la masse immobile (v(0) = 0) est soumise à une force F conduisant au déplacement x.
21. Écrire l’équation différentielle vérifiée par x.
F -kx -g dx/dt = m d2x / dt2 ; d2x / dt2 + g / m dx/dt  +k /m x = F/ m. (3).
22. Montrer que dans le cas d’une protéine de masse m = 160 × 10–24 kg, on peut écrire x(t) sous la forme :
Solution générale de (3) sans second membre :
l'équation caractéristique est : r2+g / m r +k/m = 0 ; discriminant D = (g / m)2-4k/m, positif avec ces données.
D =( g 2-4km) / m2.
r1 =-( g  +D½) / (2m) ; r2 = -( g  -D½) / (2m) ; on pose t1 = -1/r1 et t2 = -1/r2.
x= A exp(-t / t1) +B exp(-t /t2 ). A et B sont des constantes.
Solution particulière de (3) : x = F / k.
Solution générale de (3) : x=A exp(-t / t1) +B exp(-t /t2 )+F / k.
A l'instant initial : x=0 ; A + B +F/k = 0.
Vitesse dx/dt = -A/ t1 exp(-t / t1) -B/t2 exp(-t /t2 )
v(t=0)=0 : 0 = -A/ t1 -B/t2 ; B = -At2 / t1  ; A- A t2 / t1 +F/k = 0 ; A = -t1 F / (k(t1-t2 )) et B =  t2 F / (k(t1-t2 )).
x=F / k [-t1 /(t1-t2 ) exp(-t / t1) + t2 /(t1-t2 ) exp(-t /t2 )+1].
On exprimera le déplacement à l’état stationnaire x(oo) en fonction des constantes du problème. x(oo)= F/k.
23. Dessiner l’allure de l’évolution temporelle de x.
24. Quel est dans ce cas le signe de gv – ma ? Quelles forces dominent entre les forces d’inertie et les forces visqueuses ?
ma +kx+g v = F.
25. Rappeler l’expression du travail w d’une force F pour un déplacement dx.
26. Montrer que dans le cas ci-dessus on peut écrire : w = q + e + u
avec u =½kx2 l’énergie potentielle du ressort ; e =½mv2 l’énergie cinétique de la masse m ; 
 la chaleur dissipée lors du mouvement. Que signifie cette égalité ?
La conservation de l'énergie s'écrit :



.


  

menu