Thermodynamique.
Concours CPR Maroc 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie
A.
Une masse d'air supposé gaz parfait occupe un volume V0= 10 L à la pression p0 =1 bar à la température T = 298 K. On la comprime dans une transformation réversible jusqu'à la pression p1 = 5 bar. Le volume est V1. g = 1,4.
46. A température constante, la quantité de chaleur dégagée pendant la transformation est :
L'énergie interne du gaz parfait ne varie pas si la transformation est isotherme.
DU = 0 = W +Q ; Q = -W.
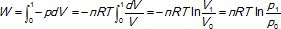
n = P0V0 / (RT) =105 *0,010 /(8,314*298)=0,4036 mol.
Q = -0,4036*8,314*298 ln5= -1609 J ~-1,61 kJ.
Réponse B.
47. En supposant la transformation adiabatique, le volume V1 et la température T1 du gaz à la fin de la transformation valent respectivement :
P1V1g=P0V0g ; V1=V0(P0 /P1)1/g = 10*0,21/1,4 =3,17 L.
T0V0g-1 = T1V1g-1 ; T1 =T0( V0 /V1)g-1=298(10 / 3,17)0,4=472 K
Réponse B.
48. En supposant la transformation adiabatique, la variation d'énergie interne du gaz vaut :
Q = 0 ; DU =W = nR / (g-1) (T1-T0)=0,4036 *8,314 /0,4 (472-298)=1460 J ~1,46 kJ.
Réponse C.
|
| .
. |
|
|
Partie B.
Un gaz parfait décrit un cycle et subit successivement une détente isotherme AB à la température T1, une détente adiabatique BC au cours de laquelle sa température passe de T1 à T2, une compression isotherme CD à T2 et une compression adiabatique DA qui le ramène à T1.
49. Le rendement du cycle s'écrit :
Second principe : sur le cycle.
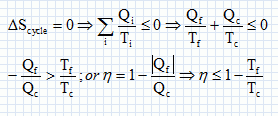
Le rendement est maximal dans le cas de la réversibilité et vaut h = 1-Tf/Tc.
h =1-T2 / T1.
Réponse D.
|
|
|
|
Partie C.
Une mole de gaz parfait diatomique ( g = 1,4) subit une évolution isotherme à T = 293 K de la pression p1 = 1 bar à la pression p2 = 2 bar.
50. La variation d'entropie du gaz parfait est :
L'entropie est une fonction
d'état : en conséquence le chemin emprunté entre l'état initial et final
importe peu ; le calcul de la variation d'entropie est fait pour une
transformation réversibble.
Variation d'entropie élémentaire : dS= dSéchangée + dScréée.
dScréée. = 0 dans le cas d'une transformation réversible.
L'énergie interne du gaz parfait ne varie pas si la transformation est isotherme.
DU = 0 = W +Q ; Q = -W.
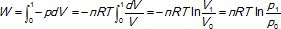
D Séchangée =Q/T = -nR ln (p1 / p2) = -8,314 ln 0,5 =5,76 J K-1. Réponse A.
|
|