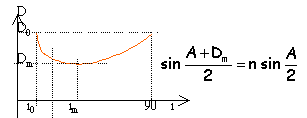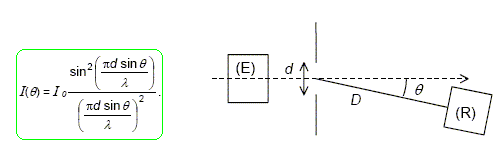Optique.
Concours CPR Maroc 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie A.
40. Prisme et minimum de déviation.
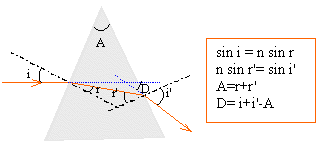
cos i di =dn sin r + n cos r dr
(1)
cos i' di' =dn sin r' + n cos r' dr'
(2)
dA= dr + dr'
(3)
dD = di + di' - dA
(4)
pour éliminer di'
on ajoute : (1)
cosr'
+ (2) cos r
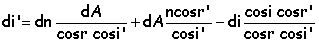
on remplace dans
(4)
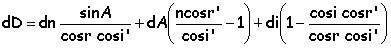
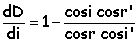
extrémum si cos i cos r' = cos i' cos
r
élever au carré et exprimer r et
r' en fonction de i et i'
soit D présente un minimum pour i =
i'
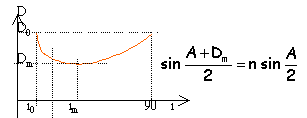
Au
minimum de déviation le trajet du rayon
lumineux est symétrique par rapport au plan
bissecteur du prisme
i = i' = im ; r = r'= ½A. Dm=2im-A.
Réponse
C.
41. Si i = 45°et A = 60°, D =50,3°. L'indice de réfraction du prisme est :
D = i +i'-A ; i +i' = D+A = 110,3° ; i' = 110,3-45 =65,3° ; r+r' =A = 60° ; r' = 60-r.
sin i' =n sin r' ; sin 65,3 = n sin (60-r)= 0,9085.
0,9085 =n(sin 60 cos r -sin r cos 60)
0,9085=n(0,866 cos r-0,5 sinr).
sin i = n sin r ; sin r = sin45 / n = 0,707 /n.
0,9085=0,866 n cos r- 0,5 *0,707.
0,866 n cos r =1,26 ; n cos r =1,457.
tan r = 0,707 / 1,457 ~0,485 ; r = 25,88°
n = 0,707 / sin 25,88 =1,62.
Réponse C.
|
| .
. |
|
|
Partie B.
Un système optique comporte une lentille convergente L1 de centre optique O1 de distance focale f'1 = 1 cm et une lentille divergente L2 de centre optique O2, de distance focale f'2 =-7 cm.
O1O2 = 9 cm.
Les lentilles ont le même axe optique principal. Un objet lumineux AB
de hauteur h = 2 cm est placé perpendiculairement à l'axe optique, 2 cm
avant la lentille convergente. On note A2B2 l'image donnée par le système.
42. Position de l'image A2B2.
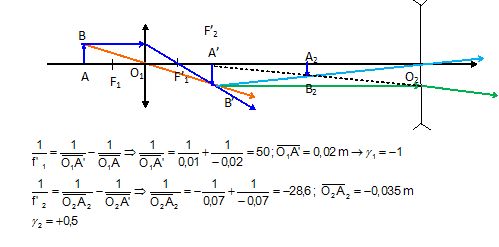
Réponse
B.
43. Le grandissement est :0,5 *(-1) = -0,5.
Réponse
B.
|
|
|
|
Partie C.
Un
réseau plan comporte N bandes transparentes rectilignes parallèles, de
même largeur b, de longueur très grande devant b, percées dans un écran
opaque. Les axes de deux bandes consécutives sont déparés par une
distance a. On éclaire ce réseau par une onde plane monochromatique de
longueur d'onde l sous incidence normale.
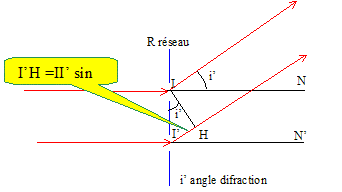
Sous incidence normale, sin i'
= kl
n avec n = 1 /a nombre de traits par millimètre et k un nombre entier.
44. Intensité diffractée à l'infini par ce réseau dans la direction angulaire i'.
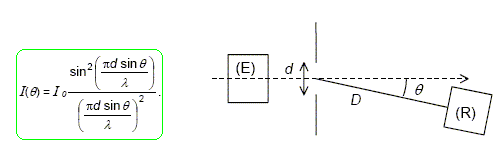
I0 étant l'intensité sur l'axe
médian à la distance D de la fente.
45. Dans le cas où a = 2b, le nombre de maxima principaux observés dans la tache centrale de diffraction est :
Le deuxième pic a une hauteur nulle. On observe un pic de part et d'autre du pic central soit trois maxima.
Réponse C.
|
|