Thermodynamique
de la transition
liquide-vapeur. Agrégation
2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Transition
de phase au collège et au lycée.
Classe de cinquième : " un palier de température apparaît lors du
changement d'état d'un corps pur".
20.
A quelle expérience cet énoncé fait-il référence ? Cet énoncé est-il
complet ?
On observe un palier de température si la pression
est constante.
Mesurer en fonction du temps la température de l'eau contenue dans un
récipient ouvert chauffé. La pression est constante, égale à la
pression atmosphérique.
-
De quels paramètres peuvent dépendre les valeurs des paliers pour les
transitions solide-liquide et liquide-vapeur ?
Les valeurs des paliers dépendent de la pression.
Transition
liquide -gaz :
La variation de température ( de l'ordre de 1°C) due à la
variation de la presion atmosphérique ( basse pression 990 hPa) et
haute pression ( 1020 hPa)ne peut pa être mise en évidence. Par contre
la diminution de pression due à l'altitude entraîne une plus
gande variation de température. En présence d'impuretés
dissoutes, on n'observe pas de palier.
La pression a peu d'impact sur la transition liquide-solide.
-
Que répondre à un élève de cinquième qui remarque qu'à température
ordinaire sous pression atmosphérique, l'eau peut se trouver à l'état
gazeux, tandis qu'il a appris que l'eau était liquide en dessous de
100°C ?
" L'eau est liquide en dessous de 100°, dans un récipient fermé ne
contenant que de l'eau, à la pression atmosphérique". Dans
une bouteille d'eau minérale remplie à ras bord et fermée, il n'y a pas
de vaporisation. Il y a évaporation à toute température sui le
récipient est ouvert.
Par contre on observe des bulles au sein du liquide à 100°C. Le liquide
devient un gaz au dessus de 100°C.
-
Proposer une expérience qui permet d'observer un palier de pression.
Enfermer un gaz dans un récipient déformable. En diminuant son volume,
on observe une augmentation de pression. Dès que la pression de vapeur
saturante est atteinte, on observe un palier de pression. Si le volume
continue à décroître, le gaz se condense. Lorsque tout le gaz est
liquide, la pression .augmente à nouveau.
21. Définir
chaleur latente de vaporisation.
Pour un corps pur à la température T, la chaleur latente est égale à la
variation d'enthalpie d'une unité de masse de ce corps passant de
l'état liquide à l'état gazeux.
- La chaleur reçue par un système détermine-t-elle seule l'état final
du système dans le cas général ? Dans le cas particulier où le système
subit une transition de phase ?
L'énergie interne d'un système est modifiée lors d'une échange de
chaleur. On peut passer d'un état à un autre suivant l'importance de
cet échange. La chaleur mise en oeuvre lors d'un changement
d'état à T et P constantes est égale à la variation d'une fonction
d'état. L'état initial et l'état final sont donc connus.
|
| .
. |
|
|
22. TP en 1ère S. Fusion de la glace.
1. Prélever une masse mi= 200 g d'eau distillée
à température ambiante.
2. Placer cet eau dans un calorimètre avec thermomètre et couvercle.
Noter la température Ti à l'équilibre. Ti=20°C
3. Prélever quelques glaçons dans le becher contenant la glace et l'eau
distillée, les sécher et les peser rapidement ; mg
= 36 g. Les introduire dans le calorimètre.
4. Agiter doucement de temps en temps. Noter l'évolution de la
température de l'eau du calorimètre otutes les minutes pendant 10
minutes..
| t
(min) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| T(°C) |
19,5 |
13 |
9,5 |
6,5 |
6,5 |
7 |
7 |
7 |
7,5 |
7,5 |
7,5 |
Noter la
température la plus basse atteinte Tmini = 6,5°C.
Exploitation
individuelle.
1. Pourquoi place-t-on les glaçons dans un becher contenant de l'eau
distillée ?
On est certain que la température des glaçons est 0°C.
2. Calculer la valeur de l'énergie cédée à la masse mi
d''eau initialement présente dans le calorimètre entre le début et
l'instant où la température minimale est atteinte. ceau
= 4,18 kJ Kg-1 K-1. Q = mi
ceau (Tmini-Ti)
= 0,200 *4,18(6,5-20)~-11,3 kJ.
3. On suppose que les transferts thermiques entre l'extérieur et le
calorimètre sont négligeables.
Estimer la valeur de l'énergie reçue par les glaçons. -Q = 11,3 kJ.
4. Quelle masse d'eau a étét formée par la fonte de la glace? En
déduire l'énergie nécessaire pour amener cette masse de 0°C à Tmini.
( 36 g d'eau ).
Q' = mg ceau
(Tmini-0) = 0,036
*4,18(6,5-0)~ 0,98 kJ.
5. Calculer l'énergie nécessaire à la fonte des glaçons.
-Q-Q' = 11,3 -0,98 ~10,3 kJ.
6. Calculer l'énergie massique de fonte de la glace en J g-1.
DHf=10,3
103 / 36 ~287 Jg-1.
Analyse des
résultats.
| Groupe |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| DHf
(J g-1) |
287 |
302 |
303 |
273 |
289 |
300 |
312 |
301 |
1. Comment
expliquer les différences de valeurs entre les différents groupes ?
Valeur moyenne 296 J g-1 ;écart type
12 J g-1.Ecart relatif entre les groupes 4%.
Les différences s'expliquent par des incertitudes de mesures en
particulier sur Tmin.
2. Quelle valeur doit être retenue ?
DHf
= 297 ± 12 J g-1.
3. La valeur de l'énergie massique donnée dans les livres est 3,3 102
J g-1. Conclure.
L'écart important est dû :
au fait que le calorimètre n'est pas parfaitement isolant thermique ;
- on a négligé la capacité thermique du calorimètre ;
- la glace peut être en partie fondue en surface.
-
Quelle(s) critiqe(s) pédagogique(s) ou quel(s) complément(s) peut-on
apporter à cet énoncé ?
Ce TP permet de réaliser un bilan énergétique et d'en déduire une
valeur parfois assez éloignée de la valeur attendue.
On peut faitre tracer T = f(t) afin de remarquer la dérive.
Choisir une température initiale qui minimise les échanges avec
l'extérieur ; estimer la capacité thermique du calorimètre ; le rapport
mg / mi doit être assez
élévé.
- Cette
méthode est-elle applicable à la détermination d'une énergie massique
d'ébullition ?
Non. Il faudrait un calorimètre étanche, déformable afin d'assurer une
pression constante lors de la vaporisation.
|
|
|
|
Thermodynamique
de la transition liquide-vapeur.
On
considère un système fermé, caractérisé par une entropie S, un volume
V, une énergie interne U. Le système est en contact avec un réservoir R
avec lequelil peut échanger du volume et de la chaleur. R est supposé
très grand, de sorte que sa température T0 et sa
pression P0 sont constantes.
23.
Le système subit une transformation pendant laquelle V varie de DV, S
de DS
et U de DU.
On définit le potentiel thermodynamique F par :
F
= U-T0S+P0V. On pourra
raisonner sur l'ensemble { système + R }.
Montrer que pour une transformation spontanée : DF = DU -T0DS+P0DV
inférieur ou égal à zéro.
L'entropie de l'ensemble isolé { système + R }augmente aucours
d'une tansformation spontanée.
DStotal
= DS +DSR
= DS
-Q/T0 avec Q chaleur reçue par le système.
Q = DU-W
avec W= -P0DV,
travail reçu par le système.
DStotal
= DS - DU / T0
-P0DV / T0.
DF
= -T0DStotal
; F
décroît pour une transformation spontanée.
24. On considère la
transformation suivante.
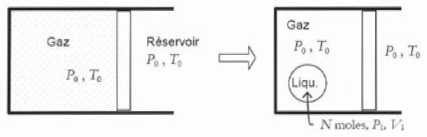
Initialement le système est
homogène, constitué de Ntot mole d'un corps pur
en phase gaz à la pression P0 et à la
température T0. A l'état final, le système est
composé de Ntot-N moles de gaz à T0
et P0 et d'une goutte de N moles de liquide de
volume V1 à la température T0
et à la pression P1. On note V0
le volume de gaz occupé initialement par les N moles ayant subi la
transformation.
Montrer que DF = GL(T0,
P1, N) -GG(T0,
P0, N) + (P0-P1)V1
où GL et GG désignent les
enthalpies libres des phases liquide et gaz.
N moles changent d'état physique.
DF
= UL(T0, P1,
N)-UG(T0, P0,
N)-T0[SL(T0, P1,
N)-SG(T0, P0,
N)]+P0(V1-V0).
DF
=[UL(T0, P1,
N) - T0[SL(T0, P1,
N) +P1V1 ]-[UG(T0, P0,
N) -SG(T0, P0,
N)+P0V0] +(P0-P1)V1.
A l'expression ci-dessus il faut ajouter une contribution due à
l'interface + gA.
Dans la suite de cette partie ( sauf question 34 ), on suppose que le
liquide est incompressible de volume molaire VL
et que le gaz est parfait. On note PV la
pression d'équilibre liquide-vapeur à la température T0.
On fait l'hypothèse que toutes les pressions sont proches de PV.
25. Montrer que le potentiel
chimique µL(T0, P1)
est donné par : µL(T0,
P1) =µL(T0,
PV) +VL(P1-PV).
Pour un liquide incompressible :
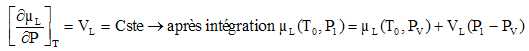
Montrer que le potentiel
chimique µG(T0, P0)
est donné par : µG(T0,
P0) =µG(T0,
PV) +RT0ln(P0/PV).
Pour le gaz parfait :
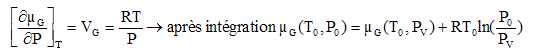
26. En déduire que :
DF
= 4/3 pr3[(P0-PV)
-RT0 / VL ln(P0/PV)+4pr2g où r
est le rayon de la goutte liquide.
Enthalpie libre G = µN avec N = 4/3 pr3/
VL.
A la pression d'équilibre PV : µL(T0,
PV) = µG(T0,
PV).
DF
= 4/3 pr3[(P0-PV)
-RT0 / VLln(P0/PV)] +4pr2g.
27. A
quelle condition peut-on négliger P0-PV devant
RT0 / VLln(P0/PV)
? Cette condition est supposée vérifiée par la suite.
La pression varie peu par rapport à PV : ln(P0/PV)~(P0-PV)/
/ PV.
RT0 (P0-PV)
/ (VLPV) =VGP0(P0-PV)
/ (VLPV) ~VG(P0-PV)
/ VL.
VG : volume molaire du gaz. VG
>> VL éloigné du point critique.
28. Représenter DF
dans les deux cas suivants P0 >PV
et P0<PV. En
déduire dans chaque cas quelle est la phase ( liquide ou gaz) la plus
stable. Ce résultat était-il prévisible ?
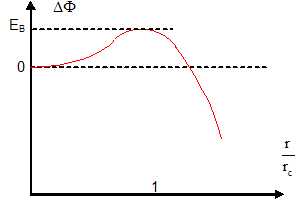
F
minimum correspond à l'état thermodynamique stable.
P0<PV : le
minimum correspond à r=0, le gaz est l'état stable, il n'y a pas de
condensation.
P0>PV : le
minimum est obtenu pour r tendant vers l'infini, le liquide est l'état
stable.
Ce résultat était prévisible, dans un diagramme (T, P), la phase
liquide occupe la partie supérieure.
29. On note rc
le rayon critique pour lequel DG(r)
est maximal. Donner l'expression de rc.
DF
= 4/3 pr3[
-RT0 / VLln(P0/PV)] +4pr2g.
Dériver par rapport à r et annuler cette dérivée : rc2RT0 / VLln(P0/PV)=2rcg.
rc = 2 gVL
/ (RT0 ln(P0/PV)).
30. Initialement le
système n'est formé que de la vapeur. Une petite fluctuation amène le
système dans l'état {vapeur + goutte de liquide de rayon r}.
Discuter l'évolution ultérieure du système suivant la valeur de r.
Comment qualifie-t-on l'état initial du système ?
Le système évolue en minimisant F.
Si r <rc, le système revient à l'état de
vapeur uniforme ; si r >rc, le système
passe à l'état liquide.
Initialement le système se trouve dans un état métastable.
31.
Exprimer la barrière d'énergie EB que doit
franchir le système pour passer de l'état initial à l'état
thermodynamique stable.
Remplacer rc par 2 gVL
/ (RT0 ln(P0/PV))
dans F puis
simplifier.
EB = 16 p g3
V2L / (3[RT0
ln(P0/PV)]2).
32.
Par analogie avec le cas d'une réaction chimique dont la cinétique est
limitée par une étape dont l'énerie d'activation est grande devant kBT,
proposer une expression de la probabilité que le gaz se
liquéfie entièrement ( à un facteur multiplificatif près).
Lors d'une fluctuation, une goutte de rayon rc
doit être créée.
La probabilité qu'une fluctuation conduise le système dans un état
énergétique EB au dessus de son état d'équilibre
est proportionnelle à exp(-EB/(kBT).
33.
Des expériences menées sur le nonane à température constante T0
ont permis de mesurer la probabilité de liquéfaction Pr à une constante
multiplicative Cte près en fonction de la
pression initiale P0.
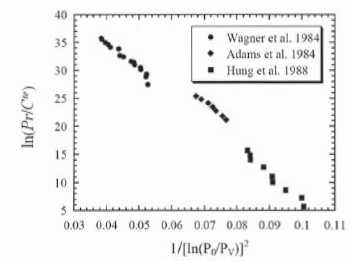
Discuter qualitativement et quantitativement ces données
expérimentales.
Pour le nonane T0 = 238K ; VL
= 0,167 10-3 m3 ; PV
= 3 mbar et g
= 28 mN m-1.
Ln Pr décroît de manière linéaire en fonction de
1/(ln (P0/PV))2,
ce qui était prévu. La valeur absolue du coefficient directeur de la
droite est proche de (40-5) / (0,105-0,03) ~470.
Coeficient directeur obtenu lors de l'étude précédente : 16 p g3
V2L / (3R2T0
3 kB) ~800,
donc du même ordre de grandeur.
34.
Pour l'instant, on s'est intéressé exclusivement au cas de la
condensation.
Le retard à la transition de phase peut-il s'observer dans le cas
inverse de la nucléation d'une bulle de gaz ( ou cavitation ) dans du
liquide sous tension ?
On observe couramment un retard lors d'une transition liquide
--> solide. |
|
|
|