Protéines fluorescentes. Agrégation 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Phénomène de fluorescence. Le diagramme de perrin-Jablonski représenté ci-desous indique les niveaux d'énergie relatifs aux différents états ( fondamental et excités ) d'une molécule organique ainsi que les temps caractéristiques (t) des différents processus. On considère que la loi de décroissance d'une population n de molécules dans un état excité est du type : n = n0 exp(-t/t). Lorsqu'une molécule est excitée par absorption dun photon, lentité moléculaire résultante ( à durée de vie très brève ), se désexcite en libérant l'énerie exédentaire par dissipation thermique ( processus non radiatif), et, dans certains cas, par émission d'un photon. La fluoresence correspond à l'émission d'un photon à partir d'un état singulet ; la phosphorescence correspond à l'émission d'un photon à partir d'un état triplet. 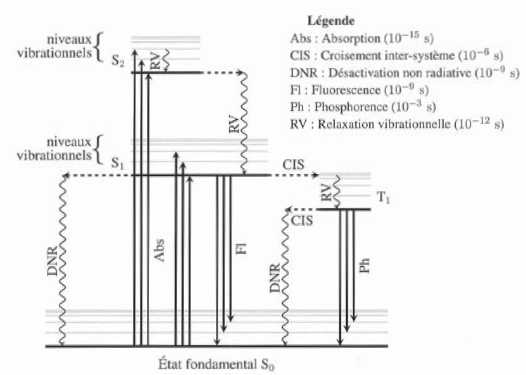Les états fondamental et excités à gauche sont des états singulets ( S , ceux de droite sont des états triplets ( T). 35. Quelle est l'origine de cette différence entre les deux types d'état S et T ? Etat singulet : tous les électrons sont appariès, lamultiplicité vaut 1. Etat triplet : deux électrons ne sont pas appariés, la multiplicité vaut 3. Les molécules organiques existent à l'état fondamental dans l'état singulet, la molécule de dioxygène existe àl'état fondamental dans l'état triplet. 36. Justifier le fait que l'état fondamental du dioxygène est de  de type triplet. 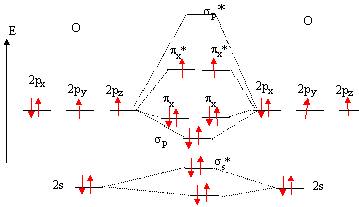Deux électrons ne sont pas appariès, la molécule est dans un état fondamental de type triplet. 37. Lorsque les photochimistes souhaitent travailler sur des entités chimiques excitées dans des états triplets, ils procèdent à des dégazages répétés des solvants de réaction. Justifier. Il faut se débarasser des gaz atmsphériques dissouts (en particulier le dioxygène). Le dioxygène peut réagir avec des espèces à l'état triplet, formées dans les réactions photochimiques, et les dégrader. . . On considère un groupe carbonyle (C=O) qui est irradié par une radiation électromagnétique de longueur d'onde appropriée. La transition électronique a pour effet de faire passer un électron d'un doublet non liant de l'atome d'oxygène vers une orbitale antiliante p* de la liaison carbonyle. La distance carbone-oxygène dans le groupe carbonyle à l'état fondamental vaut d=120 pm. 38. Quelle sera la valeur de la distance carbone-oxygène dans le groupe carbonyle dans l'état Franck-Condon ? Une transition électronique se produit sans modification de la position des noyaux dans l'entité moléculaire et son environnement. Cette distance d ne varie pas. 39. Que peut-on attendre comme modification de la distance carbone-oxygène dans le groupe carbonyle dans le premier état excité singulet ? L'indice de liaison est égal àla moitié de la différence entre le nombre d'électrons occupant les OM liantes et le nombre d'électrons occupant des OM antiliantes. Un électron non liant est passé d'une orbitale antiliante : l'indice de liaison passe de 2 à 1,5. On peut s'attendre à une augmentation de la distance carbone-oxygène du groupe carbonyle dans cet état excité. La règle empirique de Kasha indique qu'après l'absorption d'un photon par une molécule dans l'état fondamental et le peuplement résultant des états excités, l'émission radiative qui s'ensuit se produit à partir de l'état excité de plus basse énergie. 40. Justifier cette règle empirique. La molécule est excitée en 10-15 s et passe dans des états excités de différents niveaux électronique et vibrationnel, puis elle se désexcite. La relaxation vibrationelle  est beaucoup plus rapide ( 10-12 s) que la fluorescence et la désactivation non radiative (10-9 s). La relaxation vibrationnelle se produit d'abord conduisant à un état excité singulet, la fluorecence se réalise ensuite. Expérimentalement, on observe que les spectres d'émission et d'absorption sont décalés ; ce décalage est appelé déplacement de Stokes. 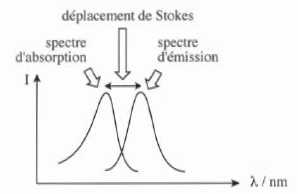41. Expliquer l'origine de ce déplacement. Le photon émis possède une énergie inférieure au photon absorbé du fait de la perte d'énergie par relaxation vibrationnelle. Eémis < Eabsorbé ; E = h c / l ; lémis > l absorbé. Inhibition de la fluorescence. Processus d'absorption d'un photon : E +hn---> E*. Il est considéré en première approximation comme indépendant de la présence des autres entités présentes dans le milieu. L'émission d'un photon par fluorescence s'écrit : E* ---> E + hn' avec v = kfl [E*]. L'entité excité peut également revenir àl'état fondamental par un procesus non-radiatif : la désexcitation thermique. On définit le rendement quantique de fluorescence FF comme le rapport de la constante de vitesse du processus de fluorescence sur la somme des constantes de vitesse de tous les processus possibles de désexcitation. Ainsi lorsque la désexcitation se produit uniquement par fluorescence ( kfl) et par voie thermique ( kth), le rendement quantique de fluorescence vaut : FF = kfl / ( kfl+kth) avec kfl+kth = 1/t0, temps de vie de l'état excité. Certaines espèces chimiques, appelées quencher ( notés Q) ou inhibiteurs possèdent la propriété d'inhiber la fluorescence. Le processus d'inhibition résulte d'une collision entre l'entité à l'état excité et le quencher avec libération d'énergie thermique ; on parle d'inhibition dynamique ou collisionelle. Ce processus s'écrit : E*+Q---> E+Q +transfert thermique. ( constante de vitesse kq) 42. Donner la molécularité et la loi de vitesse de ce processus d'inhibition. La molarité de cette étape élémentaire vaut 2 et la loi de vtesse s'écrit v = kq[E*][Q]. 43. On iradie avec un flux lumineux constant une cellule contenant l'entité E à exciter. Donner l'expression de d[[E*] /dt en présence et en absence de quencher. Absence de Q : processus de fluorescence et thermique. d[[E*] /dt =-(kth+kfl)[E*]. Présence de Q : compétition entre les processus précédents et l'inhibition :d[[E*] /dt =-(kth+kfl+kq[Q])[E*]. 44. On se place dans les conditions photostationnaires. La quantité d'entité formée par irradiation est égale à la quantité d'entité détruite par tous les processus possibles de désexcitation. Donner en présence et en l'absence de quencher, l'évolution temporelle de la concentration en entité excitée E*. d[[E*] /dt =0. 45. Etablir l'équation de Stern-Volmer écrite ci-dessous et donnant l'évolution du rapport des rendements quantiques de fluorescence (Ff0/Ff) en fonction des concentrations en qencher Q, équation dans laquelle Ff0/Ff =1+kqt0[Q]. Ff0 : rendement quantique en absence de quencher ; Ff : rendement quantique en présence de quencher. Absence de Q :  d[[E*] /[E*]=-(kth+kfl)dt. [E*] =[E*]0 exp(-(kth+kfl) t ). Présence de Q : d[[E*] /[E*]=-(kth+kfl+kq[Q])dt. [E*] =[E*]0 exp(-(kth+kfl+kq[Q]) t ). Rendement quantique : Ff0  =kfl / (kth+kfl) = kfl t0. Ff =kfl / (kth+kfl+kq[Q]) = kfl t0 / (1+t0kq[Q]). Ff0/Ff =1+kqt0[Q]. On a reporté ci-dessous les droites de Stern-Volmer pour l'inhibition de fluorescence à différentes température croissantes de T1 à T5. 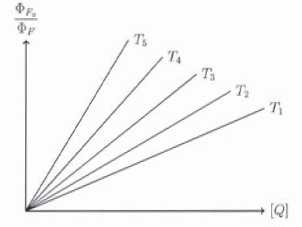46. Quel est l'effet d'une augmentation de la température sur l'inhibition de la fluorescence ? Quelle raison peut-on évoquer pour expliquer cet effet ? L'inhibition croît avec la température. Le nombre de collisions croît avec la température, la constante de vitesse kq augmente. Une deuxième forme d'inhibition de fluorescence a été observée, elle suit une loi de vitesse analogue à la précédente : Ff0/Ff =1+K[Q]. Cette inhibition est dite statique : le quencher et l'espèce àl'état excité E* réagissent l'un avec l'autre pour donner un complexe QE*, lequel ne donne pas lieu à une fluorescence mais subit une désactivation thermique. Les étapes du processus sont rassemblées dans la figure suivante : 47. Expérimentalement on observe dans ce cas que le rendement quantique  de fluorescence croît avec la température. Proposer une explication. Si le rendement croît, [QE*] diminue avec une augmentation de température. L'explication est d'ordre thermodynamique : une augmentation de température déplace l'équilibre vers la gauche.

menu