Equation
différentielle, étude d'une fonction. Bts maths groupe D 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
On
s’intéresse à une maladie dégénérative de l’oeil qui occasionne des
troubles de la vision. Afin
de freiner son évolution, deux traitements sont possibles. Dans cet
exercice, on étudie, pour
ces deux traitements, l’évolution de la quantité des principes actifs
présents dans le sang en
fonction du temps.
Partie
A : Etude du premier traitement.
Le premier traitement consiste à faire absorber au malade par voie
orale un médicament qui
libère peu à peu le principe actif qui passe dans le sang. Il est
efficace lorsque la quantité de
principe actif est supérieure ou égale à 5 mg. On admet qu’à l’instant
t = 0 la quantité de
principe actif présente dans le sang est de 1 mg.
1.
Résolution
d’une équation différentielle.
L’évolution en fonction du temps (exprimé en heures), de la quantité de
principe actif
présente dans le sang après absorption (exprimée en mg) est modélisée
par une fonction
vérifiant l’équation différentielle :
(E) : y' + 0, 1y = 2e−0,1t.
où y est une fonction de la variable t , définie et dérivable sur [0
;+oo[ et y' la dérivée de la fonction y.
(a)
Déterminer les solutions sur [0 ;+oo[ de l’équation (E0)
: y' + 0, 1y = 0.
y = A e-0,1t avec A une constante.
(b)
Soit h la fonction définie sur [0 ;+1[ par h(t) = 2t e−0,1t.
Vérifier que h est une solution particulière de (E).
h' = 2 e−0,1t- 0,2 t e−0,1t.
Repport dans (E) : 2 e−0,1t- 0,2 t
e−0,1t +0,2t e−0,1t
= 2e−0,1t.
L'égalité est vérifiée quel que soit le temps.
(c) En déduire
l’ensemble des solutions de l’équation différentielle (E).
y = A
e-0,1t + 2t e−0,1t.
(d) Déterminer la
solution de (E) correspondant au problème posé.
A
t=0, y = 1 = A ; y = e-0,1t + 2t e−0,1t.
2. Etude d'une fonction.
Soit
la fonction f définie pour tout t de l’intervalle [ 0;+oo[ par f(t) =
(2t + 1)e−0,1t .
(a)
On admet que la limite de f en +oo est 0. Interpréter graphiquement
cette limite.
La droite d'équation y =0 est asymptote.
(b)
On note f' la fonction dérivée de f et on admet que f'(t) = (1, 9 − 0,
2t)e−0,1t.
Etudier le signe de f'(t) sur l’intervalle [0 ;+oo[.
Dresser le tableau des variations de f sur [0 ;+oo[.
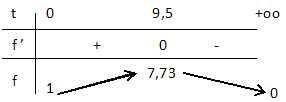
|
| .
. |
|
|
3. Application.
(a)
Au bout de combien de temps la quantité de principe actif dans le sang
sera-t-elle maximale ?
La quantité de princie actif est maximale à t = 9 h 30 min.
(b)
Sur quel intervalle de temps le médicament sera-t-il efficace ?
f(t) supérieure ou égale à 5.
| t
(heure) |
2,85 |
20 |
21,9 |
22 |
| f(t)
(mg) |
5,03 |
5,55 |
5,01 |
4,98 |
Le médicament est efficace sur
l'intervalle [2,85 ; 21,9 h ].
(c) Déterminer la
quantité moyenne de principe actif présente dans le sang entre 0 et
24 h. On arrondira le résultat au dixième. On donne :
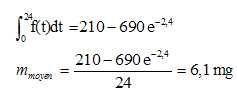
|
|
|
|
Partie
B : Etude statistique du second traitement.
Le second traitement consiste à injecter par intraveineuse un
médicament qui permet une meilleure vascularisation des vaisseaux
sanguins de la rétine. A l’instant t = 0, on injecte une dose de 1,8 mg
de médicament, appelée dose de charge. On suppose que ce procédé
diffuse instantanément dans le sang le principe actif qui est ensuite
progressivement éliminé par les reins.
1.
Administrations
répétées du médicament.
On décide de réinjecter une dose de 1,8 mg toutes les heures, dose
supportable par le patient.
Parmi les trois courbes suivantes, quelle est celle qui représente le
mieux l’évolution de la quantité de médicament présente dans le sang ?
Argumenter votre choix.
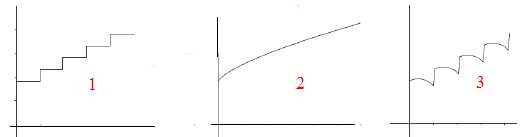
(3) convient : toutes les heures, une dose de 1,8 mg est injectée ;
elle passe très rapidement dans le sang. On bserve durant l'heure
suivante une diminution de la quantité de principe actif dans le sang.
2.
Administration
continue du médicament : recherche de la courbe de tendance.
Après avoir injecté la dose de charge de 1,8 mg, on décide
d’administrer ce médicament à l’aide d’une pompe, de manière continue,
afin de réduire le plus possible les oscillations de la quantité de
principe actif dans le sang.
L’étude consiste à déterminer l’état stationnaire (steady state) pour
ce médicament. On considère que l’état stationnaire est atteint lorsque
la différence entre la quantité limite et la quantité dans le sang est
inférieure ou égale à 1 mg.
On effectue sept mesures régulières pendant 24 h et on obtient les
relevés suivants, où qi désigne la quantité en
mg de principe actif dans le sang àl’instant ti.
| ti
(h) |
0 |
4 |
8 |
12 |
16 |
20 |
24 |
| qi
(mg) |
1,8 |
9,5 |
15,5 |
20,2 |
23,7 |
26,8 |
28,7 |
| yi |
3,53 |
3,28 |
3,02 |
2,76 |
2,51 |
2,22 |
1,99 |
On cherche à modéliser l’expression de la quantité de principe actif
dans le sang en fonction du temps. Un ajustement affine n’étant pas
judicieux, on décide de procéder à un changement de variable.
(a)
On pose yi = ln(36 − qi).
Donner les 3 valeurs manquantes dans la 3ème
ligne de ce tableau. Arrondir au centième.
Déterminer, à l’aide de la calculatrice, une équation de D la droite
d’ajustement de y en t par la méthode des moindres carrés. Arrondir les
coefficients au centième.
y = -0,065 t +3,53.
(b)
Donner une expression de la quantité q en fonction de t déduite de cet
ajustement.
-0,065 t +3,53 = ln(36-q) ; e-0,065 t +3,53
=36-q ; q = 36 -e-0,065 t +3,53 .
(c)
Un médecin affirme que l’état stationnaire est atteint en moins de
trois jours. En admettant que la quantité limite est de 36 mg, quel
argument peut-il fournir pour justifier cette affirmation ?
q(t = 72) = 35,7 mg ; q(t = 60) = 35,3 mg.
L’état stationnaire est atteint lorsque la différence
entre la quantité limite et la quantité dans le sang est inférieure ou
égale à 1 mg.
|
ans
|
|
|