Equation
différentielle, étude d'une fonction. Bts maths groupe B 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
A. Résolution
d’une équation différentielle.
On considère l’équation différentielle (E) : y"+2y′+ y = 2e−x
,
où y est une fonction inconnue de la variable réelle x, définie et deux
fois dérivable sur R, y′ la fonction dérivée de y et y′′ sa
fonction dérivée seconde.
1. a.
Résoudre dans R l’équation r 2 +2r +1 = 0.
D
= 4-4 = 0 ; r = -b/(2a) = -2 / 2 = -1.
b.
En déduire les solutions définies sur R de l’équation différentielle
(E0) : y′′ +2y′+ y = 0.
y = (Ax+B) e-x avec A et B sont
des constantes.
2. Cette question est un
questionnaire à choix multiples. Une seule réponse est exacte. Recopier
sur la copie la réponse qui vous paraÎt exacte. On ne demande aucune
justification. La réponse juste rapporte un point. Une réponse fausse
ou une absence de réponse ne rapporte ni n’enlève de point.
Une solution de l’équation différentielle (E) est donnée par la
fonction définie sur R par l’expression ci-dessous.
g(x) =2e-x ( vrai ) ; h(x) = x2
e-x ; k(x) = 2xe-x.
Les dérivées première et seconde de ces fonctions sont données
ci-dessous (ces calculs sont exacts).
g ′(x) = −2e−x ; h′(x) = (2x −x2)e−x
; k′(x) = (2−2x)e−x.
g ′′(x) = 2e−x ; h′′(x) = (x2
−4x +2)e−x ; k′′(x) = (−4+2x)e−x.
3.
En déduire les solutions de l’équation différentielle (E).
g
′′(x) +2g
′(x) +g(x) = 2e−x −4e−x +2e-x = 0, diffère de 2e−x .
h ′′(x) +2h ′(x) +h(x) = (x2 −4x
+2)e−x +2(2x −x2)e−x
+
x2 e-x =2e−x .
k ′′(x)
+2k
′(x) +k(x) = (−4+2x)e−x+2(2−2x)e−x+ 2xe-x
=0, diffère de 2e−x
.
Solution de (E) : f(x) = (Ax+B) e-x + x2 e-x.
4. Déterminer la
solution (de J’équation différentielle (E) qui vérifie les conditions
initiales f (0) = −1 et f ′(0) = 1.
f(0) = B = -1.
f '(x) = ( A-B-Ax )e-x +2xe-x
-x2e-x.
f '(0) = A-B = 1 ; A = 0.
f(x) =
( x2 -1)e-x.
|
| .
. |
|
|
B.
Étude d’une fonction.
Soit f la fonction définie sur R par f (x) = (x2
−1)e−x .
On désigne par C la courbe représentative de f. On donne la dérivée de
f : -(x2-2x-1)e-x.
Justifier par un calcul l’expression de f ′(x).
On pose u = (x2-1) et v = e-x
; u' = 2x ; v' =- e-x.
f '(x) = u' v + v' u = 2x
e-x -(x2-1)e-x
= -(x2-2x-1)e-x.
b. On rappelle
qu’une équation de la tangente à la courbe C au point d’abscisse
a est donnée par : y = f ′(a)(x −a)+ f (a).
Déterminer une équation de la tangente T à la courbe C au point
d’abscisse 0.
f '(0) = 1 ; f(0) = -1 ; y =x-1.
2. a. À
l’aide du développement limité, à l’ordre 2, au voisinage de 0, de la
fonction t --> et, déterminer le
développement limité, à l’ordre 2, au voisinage de 0, de la fonction :
x -->e−x .
et = 1 +t+½t2 +t2e(t) ;
la limite de e(t)
est nulle quand t tend vers zéro.
e-x =1-x+½x2 +x2e(x) ; la limite de e(x)
est nulle quand x tend vers zéro.
b. En déduire que
le développement limité, à l’ordre 2, au voisinage de 0, de la fonction
f est :
f (x) = −1+x +½x2+x2e(x) ;
la limite de e(x)
est nulle quand x tend vers zéro.
f
(x) = (x2 −1)[1-x
+½x2+x2e(x)] ;
f(x) = -1+x -½x2-x2e(x) +x2
-x3+½x4 +x4e(x) ;
f(x)
= -1+x
+½x2+x2e(x) à l'ordre 2. La limite de e(x)
est nulle quand x tend vers zéro.
c. Cette question
est une question à choix multiples. Une seule réponse est exacte.
Recopier sur la copie la réponse qui vous paraît exacte. On ne demande
aucune justification.
La réponse juste rapporte un point. Une réponse fausse ou une absence
de réponse ne rapporte ni n’enlève de point.
On veut justifier qu’au voisinage du point d’abscisse 0, la courbe C
est au dessus de la droite T . Recopier sur la copie la justification
qui vous paraît exacte.
−1+x est positif au voisinage de 0. ( faux ).
½x2 est positif au
voisinage de 0. ( vrai ).
x2e(x)est positif au voisinage de 0.
|
|
|
|
C. Calcul
intégral.
1.a.
On donne une primitive sur R de la fonction f : F = -(x+1)2
e-x.
Justifier ce résultat.
On pose u = -(x+1)2
et v = e-x ; u'
= -2(x+1) ; v' = -e-x.
F' = u'v +v'u = -2(x+1)e-x+(x+1)2 e-x =(x2-1)
e-x =
f(x).
b.
Calculer :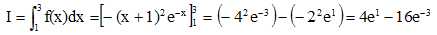
2.
Cette question est un questionnaire à choix multiples. Une seule
réponse est exacte. Recopier sur la copie la réponse qui vous paraÎt
exacte. On ne demande aucune justification. La réponse juste rapporte
un point. Une réponse fausse ou une absence de réponse ne rapporte ni
n’enlève de point. On admet que f (x) est positif pour x dans
l’intervalle [1 ; 3].
I est une mesure, en unités d’aire, de l’aire de la partie du plan
comprise entre l’axe des abscisses, la courbe C et les droites
d’équation
x = 1 et x = 3. ( vrai ).
I est une mesure, en cm2 de l’aire de la partie
du plan comprise entre l’axe des abscisses, la courbe C et les droites
d’équation
x = 1 et x = 3. ( faux ).
I est une mesure, en unités d’aire de l’aire de la partie du plan
comprise entre l’axe des abscisses, la courbe C et les
droites d’équation y = 1 et y = 3. ( faux ).
|
ans
|
|
|