Probabilités,
loi binomiale, loi normale. Bts maths groupe A 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
On
s’intéresse à un dispositif comportant deux composants électriques A et
B montés en parallèle. Si un seul de ces deux composants est
défaillant, le dispositif continue à fonctionner.
Partie
A.
Dans cette partie, on étudie la durée de vie de ce dispositif. La durée
de vie de chaque composant est une variable aléatoire.
1.
On désigne par t un nombre réel strictement positif. On admet que la
probabilité p(t ) que le composant A ait une durée de vie strictement
inférieure à t est donnée par la relation suivante.
Calculer la probabilité, arrondie à 10−2, que le
composant A ait une durée de vie strictement inférieure à 1 000 heures.
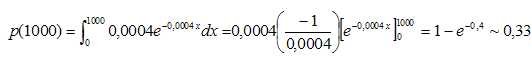
2.
Sur le document réponse 2 est donné l’arbre pondéré décrivant la
situation du dispositif au bout de 1 000 heures.
C1 désigne l’événement « le composant A est en
état de fonctionnement » et C2 désigne
l’événement « le composant B est en état de fonctionnement ».
(a)
Compléter l’arbre du document réponse 2 et indiquer le détail des
calculs des probabilités dans la colonne « Probabilités ».

(b)
Déterminer la probabilité de l’événement C2.
p(C2)=0,2211 +0,4489 =0,67.
(c)
Les événements C1 et C2
sont indépendants ? Justifier la réponse.
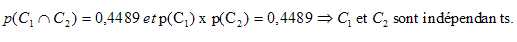
(d)
Calculer la probabilité, arrondie à 10−2, qu’au
bout de 1 000 heures, le dispositif soit en état de fonctionnement.
Le dispositif ne fonctinne pas
si les deux composants A et B sonr défaillants.
1-0,1089 =0,8911 ~0,89.
|
| .
. |
|
|
Partie B.
Dans cette partie, les résultats approchés seront arrondis à 10−3
près.
Une entreprise produit en grande série le composant A dont il est
question dans la partie A. Une étude statistique permet d’admettre que
la probabilité qu’un composant ait une durée de vie supérieure à 1 000
heures est 0,67. Les durées de vie des composants sont indépendantes
les unes des autres. Pour un échantillon de 50 composants, on note X la
variable aléatoire égale au nombre de composants ayant une durée de vie
supérieure à 1 000 heures.
1.
On admet que X suit une loi binomiale. Préciser les paramètres de cette
loi.
n = 50 ; p =
0,67 ; q = 0,33.
2.
Calculer la probabilité p(X = 42).
p(X=42) = C4250 p42
q50-42 =0,00374.
3.
Ci-dessous est donné un extrait du tableau, obtenu à l’aide d’un
tableur, donnant les valeurs des probabilités p(X <=k), où k
désigne un nombre entier naturel appartenant à l’intervalle [0 ; 50].
À l’aide de ce tableau, déterminer la probabilité que le nombre de
composants ayant une durée de vie supérieure à 1 000 heures parmi cet
échantillon soit strictement supérieur à 42.
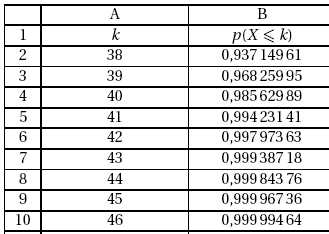
p(X
>42) =1-0,997973 ~0,002.
|
|
|
|
4. Sur
l’annexe, le diagramme en bâtons représente les valeurs de p(X
<=k) en fonction de k.
(a)
À l’aide de ce diagramme, déterminer le plus petit nombre entier
naturel k1 tel que p (X <=k1)
> 0,025,
puis le plus petit nombre entier naturel k2 tel
que p (X<=k2) > 0,975.
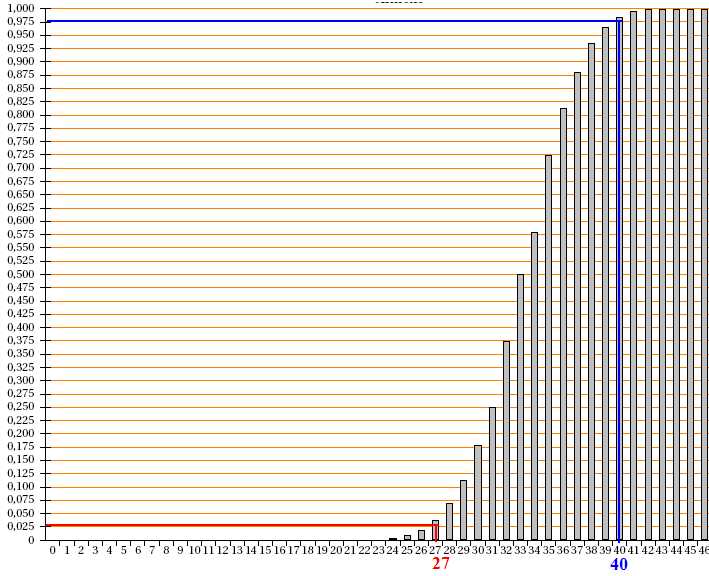
k1=27 ; k2 = 40.
(b)
Peut-on affirmer : « le nombre de composants dont la durée de vie est
supérieure à 1 000 heures appartient à
l’intervalle [27 ; 40] avec une probabilité supérieure à 0,95 » ?
Justifier la réponse.
p(27<= X <=40) =0,975-0.025=0,95. L'affirmation est vraie.
Partie
C.
Dans cette partie, on décide d’approcher la loi de la variable
aléatoire X par la loi normale de moyenne 33,5 et d’écart type 3,3.
On note Y une variable aléatoire suivant la loi normale demoyenne µ =
33,5 et d’écart type s
= 3,3.
1.
Justifier le choix des paramètres µ et s.
µ= np = 50*0,67 = 33,5 ; s =
(npq)½ =(30*0,67*0,33)½
=3,3.
2.
Calculer la. probabilité P(Y <=42) arrondie à 10−2.
P((Y-m) / s
<=(42-33,5) / 3,3) =P((Y-m) / s
<=2,57). Les tables donnent : P(Y <=42)~ 0,99.
3.
Déterminer la plus petite valeur, arrondie à 10−1,
du nombre réel a tel que p(33,5−a <= Y <= 633,5+a)
>0,95.
les
tables donnenet t = 1,96 et a = 1,96*3,3 =6,5.
|
|