Descente
à ski, dynamique des fluides, lunette afocale. Bts géomètre
2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Descente
à ski (8
points).
Le skieur avec son équipement sont modélisés par un solide de masse m
dont on étudie le
mouvement du centre de gravité G.
Cas de la descente :
Le skieur part sans vitesse initiale d’un point A et descend une piste
de longueur AB faisant un angle a avec
l’horizontale. Les forces de frottements sont négligées sur cette
portion.
A.1.
Définir le système et le référentiel d’étude.
Le système est le skieur et son équipement. Le référentiel est le
référentiel terrestre supposé galiléen.
A.2.
Donner les expressions de l’énergie mécanique EmA
et EmB du skieur respectivement
aux points A et B. On prendra comme référence d’énergie potentielle de
pesanteur le point B.:
En A, l'énergie mécanique est sous forme potentielle EmA
= mgAB sin a.
En B, cette énergie mécanique est sous forme cinétique : EmB
= ½mv2B.
A.3.
En appliquant le théorème de l’énergie mécanique, calculer la vitesse VB
du skieur au
point B. a
= 5,7° ; AB = 200 m.
En absence de frottement, l'énergie mécanique se conserve.
mgAB sin a = ½mv2B.
vB =(2gAB sin a)½
=(400*9,8 sin 5,7)½ =19,73 ~20 m/s.
A.4. En réalité, le
skieur arrive au point B avec une vitesse V'B
=16 m/s inférieure à VB. Proposer
une cause pour expliquer cette différence.
L'énergie mécanique diminue du travail des frottements.
Cas de la
montée :
Au point B, le skieur aborde une montée régulière de longueur BC
faisant un angle ß avec
l’horizontale. Au point C se trouve un guichet de remontées mécaniques.
Dans cette partie les frottements ne sont plus négligés.
A.5.
Faire le bilan des forces agissant sur le système et les représenter
surun schéma.
Le skieur est soumis à son poids, aux forces de frottements
et à l'action du plan.
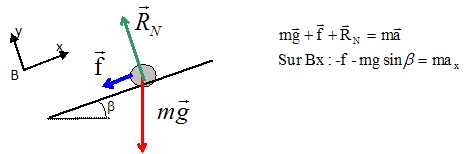
On prend le point B comme origine d’un repère (B ; x , y).
A.6.1.
Appliquer le principe fondamental de la dynamique au système skieur et
déterminer
l’expression de la composante ax(t) du vecteur
accélération sur l’axe x.
A.6.2.
Par intégrations successives, déterminer la composante vx(t)
du vecteur vitesse et la
composante x(t) du vecteur position.
ax= -(f/m+gsin ß).
vx = -(f/m+gsin
ß)t + vBx.
x = -½(f/m+gsin ß)t2
+ vBxt.
A.7. Exprimer la
durée Dt
nécessaire au skieur pour s’immobiliser. Vérifier qu’elle est égale
à 13 s. ß =2,9° ; BC = 100 m ; f = 60 N ; m=80 kg.
f/m+gsin ß=60/80 +9,8
sin2,9~1,25 m s-2.
-(f/m+gsin ß)Dt + vBx =0 ; Dt =16
/ 1,25 =12,8 ~13 s. .
A.8. Calculer la
distance d qu’il a alors parcourue.
d = -0,5*1,25*12,82+16*12,8 =102 m.
A.9.
Le skieur atteindra-t-il le guichet ?
d > BC, le guichet est atteint.
|
| .
. |
|
|
Alimentation
du lave-linge du gîte (6 points)
Pour pouvoir utiliser le lave-linge situé au premier étage du gîte, il
est nécessaire d’installer
une
pompe immergée dans la cuve de récupération d’eau de pluie. L’objectif
de cette partie est de déterminer la puissance utile de cette pompe.
L’eau
est considérée comme un fluide parfait et le régime est permanent.
Données:
Masse volumique de l’eau : r =
1,0×103 kg.m-3 ;
Intensité de la pesanteur: g = 9,8 m.s-2;
pression atmosphérique p0 = 1,0× 105
Pa ;
Equation de Bernoulli : p +½rv2+rgz=cste.
Volume du réservoir du lave-linge : V = 20 L ;
H =AC= 6,0 m, hauteur d'eau entre le lave linge C et le niveau
supérieur d'eau A dans la citerne.
h =AB= 2,0 m, hauteur d'eau entre la pompe B et le niveau
supérieur d'eau A dans la citerne.
Section de la canalisation S = 2,5 cm2 ;
Vitesse dans la canalisation, quand le débit est constant : v = 2,0 m.s-1;
Puissance mécanique reçue par une turbine : Pm =
(pentrée – psortie).qv
pentrée : pression de l’eau à l’entrée de la
turbine,
psortie : pression de l’eau à la sortie de la
turbine.
Les
dimensions de la citerne sont beaucoup plus grandes que celles de la
section S de la canalisation.
B.1.
Donner la valeur de la pression pA au point A.
L'eau est en contact avec l'air dans la citerne : pA
=
p0 = 1,0× 105 Pa.
B.2. Calculer la
pression pB au point B situé au fond de la cuve.
pB = pA +rgh =1,0×
105 +1000*9,8*2,0 =1,196 105
~1,2 105 Pa.
B.3. Quelle
approximation peut-on faire sur la vitesse VA du
fluide au point A?
La conservation du débit volumique conduit à VA ~0, la
surface de l'eau dans la citerne étant très supérieure à la section de
la canalisation.
B.4. Exprimer, puis
calculer le débit volumique Qv de l’eau dans la
canalisation.
Qv =v S = 2,0 *2,5 10-4 =
5,0 10-4 m3 /s = 0,5 L/s.
B.5.
En déduire la durée Dt
de remplissage du réservoir de volume V.
V / Qv = 20 / 0,5 = 40 s.
B.6.1.
Le lave-linge se situe à une hauteur H+h au-dessus de la pompe. En
utilisant l’équation de Bernoulli entre le point A et le point C,
déterminer la valeur de la pression pC au point
C.
pA +½rvA2+rgzA=pC
+½rvC2+rgzC=cste.
p0
+0+rgzA=pC
+½rv2+rgzC
;
pC
=p0 -½rv2+rg(zA-zc)=1,0×
105 -500*4-1000*9,8*6=3,92 104
~3,9 104 Pa.
B.6.2. Déterminer la
puissance Pm nécessaire à la pompe pour faire
fonctionner le lave- linge.
Pm = (pentrée
– psortie).Qv =(pB-pC)Qv
=(1,2 105 -3,92 104 )5,0 10-4
=40,4 ~40 W.
|
|
|
|
Lunette afocale.
Pour suivre une compétition du ski, l’étudiant dispose d’une petite lunette d’observation.
Données :
f ’1 = 10 cm ; f’2 = 4,0 cm ; O1O2 =13 cm.
La lunette est constituée d’un objectif L1 de distance focale f ’1 et de centre optique O1, et d’un oculaire L2 de distance focale f’2 et centre optique O2.
C.1. Définir une lunette afocale.
Les foyers de la lunette afocale sont rejetés à l'infini.
Soit un objet lointain ( à l'infini ) : lorsque l'image définitive est à l'infini, le système est dit afocal.
C.2. Une personne myope peut-elle utiliser une lunette afocale ? Pourquoi ?
Non. L'oeil myope est trop convergent et l'image d'un objet à l'infini se forme à l'avant de la rétine.
C.3. La petite lunette de l’étudiant, peut-elle être considérée comme afocale? Justifier.
Non. Le foyer image de l'objectif n'est pas confondu avec le foyer objet de l'oculaire. O1O2 diffère de f'1+f'2.
C.4. L’objectif de la lunette donne d’un objet AB situé à l’infini, une image intermédiaire A1B1. Où se situe l’image A1B1 par rapport à l’objet ?
L'image A1B1 de l'objet à l'infini se situe dans le plan focal image de l'objectif.
C.5. Placer sur un schéma, la lentille L2 avec ses foyers ainsi que le foyer image F’1 de L1.
Construire l'image A1B1 et l'image définitive A’B’ donnée par L2, à partir des deux rayons lumineux représentés.
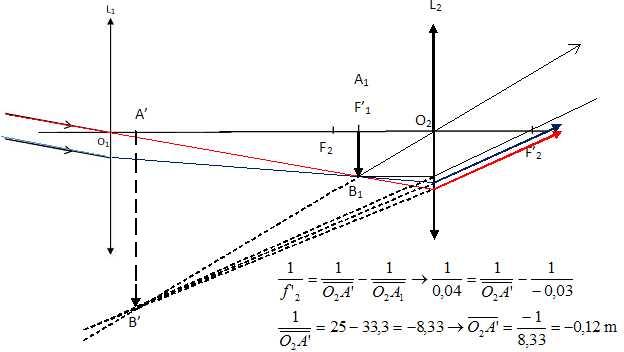
C.6. Quelle est la distance entre la lentille L2 et l’image A1B1 ?
A1B1 se trouve 3,0 cm avant L2.
C.7. Déterminer, par le calcul, la position de l’image A’B’ par rapport à L2. Quelle est la nature de cette image ? L'image est virtuelle.
C.8. Une personne myope a un P.P. situé à 18 cm et un P.R. situé à 2,0 m.
Peut-elle voir nettement l’image A’B’ en plaçant son oeil contre l’oculaire ?
Non, l'image A'B' est à 12 cm de l'oculaire.
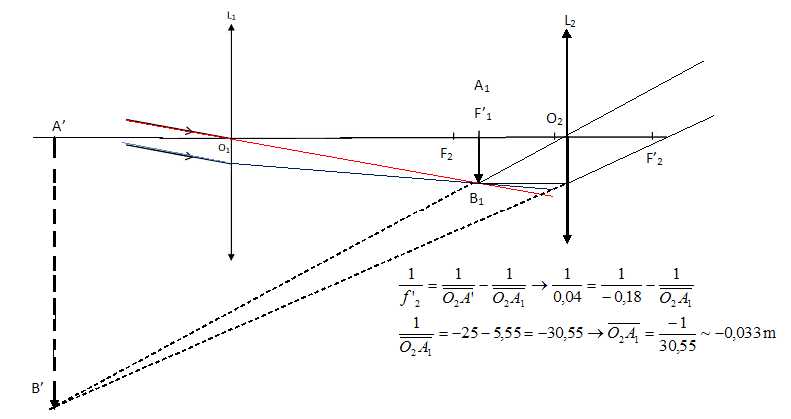
C.9. Faut-il augmenter ou diminuer O1O2 pour que la personne myope puisse observer nettement l’image à travers la lunette ?
L'image définitive A'B' doit se trouver 18 cm devant l'oculaire. Il faut augmenter O1O2.
|
|
|
|