Construction d'une
maison passive. Bac
S Liban 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Isolation et chauffage.
L’étude porte sur une maison, sans étage et de surface habitable 68 m2,
dont
l’isolation du sol, des murs extérieurs et des combles (espaces sous la
toiture) est
prévue selon les données du tableau suivant :
|
Surface
(m2)
|
Matériaux
|
Epaisseur
( cm)
|
Conductivité
thermique l
W m-1 K-1.
|
Résistance
thermique (SI)
|
Sol
|
70
|
mortier
chaux
|
25
|
0,17
|
0,021
|
Vitres
|
15
|
triple
vitrage
verre / air
|
3,6
|
0,023
|
0,10
|
Combles
|
79
|
cellulose
|
1,3
|
0,35
|
0,053
|
chanvre
|
20
|
0,048
|
Murs
ext
|
85
|
Enduit
plâtre
|
1,5
|
0,50
|
|
Briques
platrières
|
5,0
|
0,80
|
|
Liège
|
6,0
|
0,040
|
|
Briques
creuses
|
20
|
0,60
|
|
Enduit
chaux/sable
|
2,5
|
1,05
|
|
Définition
d’une maison passive.
On dit d’une maison qu’elle est passive lorsque ses besoins en
chauffage sont inférieurs à 15 kWh par m² habitable et par an contre
250 à 300 kWh par m² habitable et par an en moyenne pour les besoins en
chauffage d’un bâtiment classique.
1 kWh correspond à 3,6 MJ.
D’après le site http://fr.ekopédia.org
Résistance thermique d’une
paroi d’isolation.
La résistance thermique Rth d’une paroi plane a pour
expression : Rth = e / (lS)
où e est l’épaisseur du matériau (m), l la conductivité thermique
caractérisant le matériau
(W.m-1.K-1) et S la surface de la paroi (m²).
En pratique, une paroi est constituée de plusieurs couches de matériaux
d’épaisseur
et de conductivité différentes. Dans ce cas, les résistances thermiques
de chaque couche s’additionnent.
Flux thermique.
Le flux thermique F exprimé en watt (W), est
l’énergie transférée à travers une paroi par unité de temps. Son expression est : F = Q / Dt où Q est l’énergie thermique (J) et Dt le temps (s).
Lorsque les températures
extérieure Te et intérieure Ti sont constantes au
cours du temps, avec Ti
> Te, le flux thermique peut s’exprimer aussi par : F = (Ti-Te)
/ Rth.
|
| .
. |
|
|
Déterminer, par analyse dimensionnelle,
l’unité d’une résistance thermique.
e s'exprime en mètre et S en m2. l s'exprime en W m-1 K-1.
Rth = e / (lS) s'exprime en W-1K.
Pour une
surface donnée à isoler, expliquer qualitativement dans quel sens doivent évoluer les
caractéristiques d’une paroi pour augmenter l’isolation de l’habitation.
Pour une différence de température Ti-Te constante, le flux thermique est d'autant plus faible que la résistance thermique de la paroi est plus grande.
Choisir un isolant de faible conductivité thermique et augmenter son épaisseur.
Calculer la
résistance thermique des murs extérieurs Rm , en précisant l’unité.
Rm =(1,5 10-2 / 0,50 +5,0 10-2 / 0,80 +6,0 10-2 / 0,040 +0,20 / 0,60 +2,5 10-2 / 1,05) / 85
Rm =(0,03 + 0,0625 + 1,5 + 0,333 + 0,0238) / 85 =2,293 10-2 ~2,3 10-2 W-1 K.
Pour obtenir une
résistance thermique identique à celle des combles, quelle devrait être la valeur de
l’épaisseur d’une couche de laine de verre de conductivité thermique
llv = 0,038 W.m-1.K-1 ?
0,053 = e /(0,038*79) ; e =0,159 m = 16 cm.
|
.
|
|
Dans la région où est prévue la construction de la maison, la température moyenne du sol en hiver est d’environ 10°C et la température de l’air extérieur, 4°C.
Un poêle à bois maintient la température intérieure de la maison constante à Ti = 19°C. Pendant une journée, les valeurs des transferts thermiques sont alors :
- pour les murs extérieurs : Qm = 56 MJ ;
- pour les vitres : Qv ;
- pour le sol : Qs = 37 MJ ;
- pour les combles : Qc = 24 MJ.
Préciser le sens dans lequel s’effectuent les transferts thermiques.
Les transferts thermiques s'effectuent du corps chaud ( intérieur) vers le corps froid ( extérieur de la maison).
Calculer Qv puis en déduire la valeur de la chaleur fournie par un poêle à bois pendant une journée.
Qv =(Ti-Te) Dt / Rvitre = (19-4) *24*3600 / 0,10 =1,296 107 J ~13 MJ.
Qtotal = 56 + 13 +37 +24 =130 MJ ou 130 /3,6 ~36 kWh.
Dans ces conditions, si, par an, la période de chauffage dure 100 jours, peut on considérer la maison comme passive ?
36 *100 = 3600 kWh pendant 100 jours de chauffage ; 3600 / 68 = 53 kWh m-2 an-1, valeur supérieure à 15 : la maison n'est pas passive.
Incident sur le chantier.
Une grue soulève un sac de sable. Le câble cède lorsque le sac est à
une hauteur h par rapport au sol. Le sac tombe alors en chute libre
avec une vitesse initiale supposée nulle. Au même moment un technicien,
équipé des protections réglementaires et situé à une distance d du
point de chute du sac, se déplace à vitesse constante en direction du
point d’impact du sac avec le sol. Le sac et le technicien sont repérés
par leurs centres respectifs.
Le référentiel terrestre est supposé galiléen et on lui associe le
repère (O, i , j ), O point d’impact du sac de sable avec le sol, i
horizontal et j vertical vers le haut.
Le technicien se déplace donc parallèlement avec l’axe des x.
Données :
- intensité de la pesanteur : g = 9,8 m.s-2 ; hauteur
initiale du centre du sac de sable : h = 6,2 m ; distance initiale
entre le technicien et le point de chute du sac de sable : d = 2,5 m ;
- vitesse de déplacement du technicien : vtech = 1,1 m.s-1.
Faire un schéma de la situation initiale sans souci d’échelle en
représentant notamment le vecteur vitesse associé au déplacement du
technicien ainsi que les distances h et d.
Montrer que, selon l’axe vertical, l’équation horaire du mouvement du centre du sac de sable est : ys = - 4,9 t 2 + 6,2 avec ys en mètre et t en seconde.
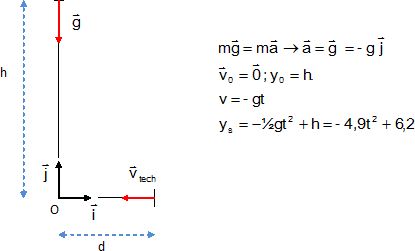
Cette situation entraîne-t-elle un risque d’accident corporel sur le chantier pour le technicien ?
Durée de la chute : t = (6,2 / 4,9)½ =1,12 ~1,1 s.
Distance parcourue par le technicien en 1,1 s : 1,1 *1,12~1,2 m. Le technicien se trouve à 1,3 m du point d'impact. Donc pas d'accident.
|
|
|