Les
cinémomètres.
Bac S Antilles 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
La
mesure de vitesse intervient dans un très grand nombre de procédés
technologiques dans des
domaines très variés : industrie, médecine, sport, transport,
aérospatiale, … Les dispositifs de mesure de vitesse sont généralement
appelés cinémomètres. Les cinémomètres les plus courants peuvent être
classés en deux catégories : les « cinémomètres Doppler » et les «
cinémomètres laser ». Cet exercice s’intéresse à certains aspects du
fonctionnement et de l’utilisation de ces deux types d’appareils pour
mesurer la valeur de la vitesse d’une "cible" dont la nature dépend du
domaine d’application.
Cinémomètre
Doppler.
Ce type d’appareil utilise une onde électromagnétique monochromatique.
Il comprend essentiellement : un émetteur qui génère une onde de
fréquence f0 = 24,125 GHz, un récepteur
qui reçoit cette onde après réflexion sur la "cible" et une chaine de
traitement électronique qui
compare le signal émis et le signal reçu. Si la "cible" visée a une
vitesse non nulle par rapport au cinémomètre, l’appareil produit un
signal périodique dont la fréquence, appelée « fréquence Doppler », est
proportionnelle à la vitesse de la "cible".
Données :
Relation, en première approximation, entre la « fréquence
Doppler » et la vitesse de la "cible" :
fD =2f0 vr
/ c.
fD : fréquence Doppler ; f0
: fréquence de l’émetteur ;
vr : vitesse relative à la "cible" par rapport à
l’émetteur ; c : vitesse de la lumière dans le vide
Célérité des ondes électromagnétiques dans le vide ou dans l’air : c =
3,00 108 m.s-1.
Les cinémomètres Doppler utilisent l’effet Doppler. Expliquer
en quelques lignes en quoi
consiste ce phénomène.
On appelle
effet Doppler la modification de la fréquence des phénomènes
périodiques lorsque les systèmes échangeant des signaux ont un
mouvement relatif.
Lorsqu'une ambulance
munie d'une sirène s'approche d'un observateur immobile, le
son perçu est plus aigu ; il devient plus grave lorsque la sirène
s'éloigne.
Un cinémomètre Doppler immobile est utilisé
pour mesurer la vitesse d’une "cible" qui s’approche
de lui. Les ondes électromagnétiques émises sont réfléchies par la
"cible" avant de revenir au
cinémomètre.
La figure ci-dessous modélise de manière très simplifiée l’allure des
ondes réfléchies par cette "cible", notée C. Déterminer, en explicitant
le raisonnement suivi, si le cinémomètre Doppler est située au point A
ou au point B.
Lorsque la cible se rapproche de l'émetteur, la fréquence percue est plus grande ; la longueur d'onde est donc plus faible. La longueur d'onde est mesurée entre deux crètes ( deux cercles) consécutives. Le cinémomètre Doppler est donc en A.
|
| .
. |
|
|
Un cinémomètre Doppler est utilisé pour mesurer la vitesse des balles de tennis lors des
principaux tournois internationaux comme celui de Roland Garros. Au cours de ce tournoi, lors
d’un service, l’appareil mesure une fréquence Doppler de valeur fD = 7416 Hz.
Calculer la valeur de la vitesse de cette balle.
fD =2f0 vr
/ c ; vr =
fD c /(2f0 ) =7416 *3,00 108 /(2*24,125 109)=46,1 m / s.
soit 46,1 *3,6 ~166 km/h.
Ce résultat est-il cohérent avec celui affiché 166 km/h. prise lors de ce service ?
Cette valeur est cohérente avec l'affichage.
|
.
|
|
Cinémomètre laser.
Le
principe de la mesure de vitesse grâce à cet instrument est basé sur
une mesure de la distance séparant la "cible" du cinémomètre laser. On
mesure le temps mis par une impulsion laser pour atteindre la "cible"
visée et revenir au cinémomètre après réflexion. Un compteur
électronique de temps est déclenché lorsque l’impulsion est émise par
le laser et arrêté lorsque l’impulsion « retour » est détectée.
Connaissant la durée d’un aller-retour ainsi que la vitesse de la
lumière, on en déduit la distance laser-cible. Pour connaître la
vitesse de la "cible", il suffit de répéter le processus de mesure de
distance à des intervalles de temps fixes.
Données :
Valeur de la longueur d’onde de l’onde électromagnétique utilisée par un cinémomètre laser : l = 904 nm
Durée entre l’émission de deux impulsions laser consécutives : T = 100 μs.
Expliquer le principe de l’émission stimulée et donner les principales propriétés du laser.
À quel domaine spectral appartient l’onde électromagnétique utilisée dans le radar laser étudié ?
Le faisceau laser est très directf ; la lumière émise est quasi-monochromatique
; la puissance délivrée par unité de surface est très grande.
Le laser émet un rayonnement à 904 nm. Le
domaine visible s'étend de 400 nm à 800 nm. Le laser émet donc dans
le proche infrarouge.
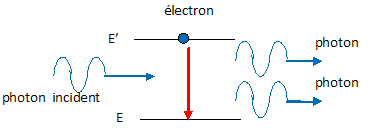
L’émission stimulée d’un atome ou
d’une molécule donne un nouveau photon qui a
exactement les mêmes fréquence, phase et
direction que le photon incident ; dans un laser, cela se
fait sur un très grand nombre d’atomes ou
molécules identiques. Un laser émet une onde
lumineuse intense dont la direction, la fréquence et
la phase sont très bien déterminées. (
lumière cohérente).
Dans
un processus de production industrielle, un cinémomètre laser en cours
de réglage a effectué très rapidement une série de 10 mesures à
intervalle de temps fixe. On obtient les
résultats suivants :
| Mesure n° | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | v(m / s) | 3,4 | 3,8 | 3,9 | 3,7 | 3,6 | 3,7 | 3,5 | 3,8 | 3,7 | 3,6 |
Évaluer le résultat de la mesure en faisant apparaitre la valeur de l’incertitude avec un niveau de confiance de 95 %.
Moyenne : vmoy =3,67 m / s ; écart type s =0,15 ; nombre de mesure N = 10.
Incertitude de mesure : Vx =2 s / N½ =2*0,15 / 10½=0,095 m / s.
v = vmoy ±Vx = 3,7 ±0,1 m / s.
Pour
le processus considéré, on souhaite disposer d’une incertitude relative
inférieure ou égale à 3 %. Cette condition est-elle vérifiée pour le
résultat précédent ?
Vx / vmoy= 0,1 / 3,7 = 0,027 ~2,7 % ; la condition est vérifiée.
Afin
de déterminer la vitesse d’une "cible", le cinémomètre radar réalise
plusieurs mesures de durée de parcours d’impulsions lumineuses.
Pour deux impulsions successives émises par le cinémomètre laser, montrer que la vitesse v de la "cible" s’écrit :
v = c(t-t') / (2T).
v : vitesse du véhicule-cible ; c : vitesse de la lumière ; T : durée écoulée entre deux impulsions successives ;
t : durée mise par la première impulsion pour parcourir un aller-retour ;
t’ : durée mise par la deuxième impulsion pour parcourir un aller-retour.
d : distance de la cible au laser à t = 0.
2d = c t ; en T seconde, la cible parcourt la distance v T :
2(d-vT) = c t’ ;
c t - 2vT =c t’ ; v = c(t-t') / (2T)
Montrer
en raisonnant sur les ordres de grandeur, qu’il est techniquement très
difficile de réaliser une mesure de la différence de durées |t-t' |. Expliciter le raisonnement.
d est de l'ordre de la centaine de mètre ; T est de l'ordre de 10-4 m ; v est de l'ordre de la dizaine de mètre par seconde.
|t-t' | est de l'ordre de 2vT / c = 20*10-4 / (3 108) ~ 10-12 s.
Cette durée est trop faible pour être techniquement mesurée.
|
|