Système de 2 points matériels en interaction gravitationnelle, concours
général 2000.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Etude
d'un système de deux points matériels en interaction gravitationnelle,
isolé dans l'espace. Généralisation au cas de deux astres à symétrie
sphérique.
Que
peut-on dire du mouvement du centre d'inertie G de ce système
?
Un
système isolé n'est soumis à aucune force extérieure. D'après le
théorème du centre d'inertie, dans un référentiel galiléen, le centre
d'inertie du système est animé d'un mouvement rectiligne uniforme.
. On note O1 et O2 les
points matériels ; ml, m2
leurs masses respectives et D la distance O1O2.
D'une manière
générale, les grandeurs relatives aux deux points seront repérées par
l'indice i prenant les valeurs i = 1 ou i = 2.
Exprimer
les vecteurs GO1 et GO2 en
fonction du vecteur D = O1O2 et des
masses m1 et m2.
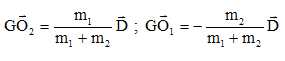
Montrer
qu'il existe un référentiel galiléen RG où G est
immobile. Définir ce référentiel. C'est celui qui sera
utilisé pour la suite de l'étude.
On
note R un référentiel galiléen. Tout référentiel en translation
rectiligne uniforme par rapport à R et lui même galiléen dans le
référentiel barycentrique G est immobile.
Soit G la constante de gravitation universelle. Donner les
expressions des forces Fi qui
s'exercent sur les points Oi en
fonction de G, m1, m2 et D.
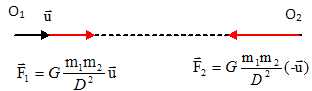
Quelles
sont les vecteurs accélérations a1 et a2 de O1 et O2
(respectivement) dans RG
?
La seconde loi de Newton conduit à :
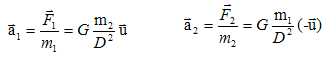
On étudie le cas particulier où les trajectoires de O1
et de O2 dans RG sont des
cercles de centre G et de rayons respectifs R1 et
R2. Montrer
que les mouvements de O1 et de O2 dans RG sont
uniformes.
Faire un schéma clair des trajectoires de O1 et O2
dans RG et de leurs positions respectives sur
ces trajectoires.
Les accélérations étant centripètes, les accélérations tangentielles dvi/dt
sont nulles ; en conséquences les vitesses vi
sont constantes : le mouvement de chaque point est uniforme.
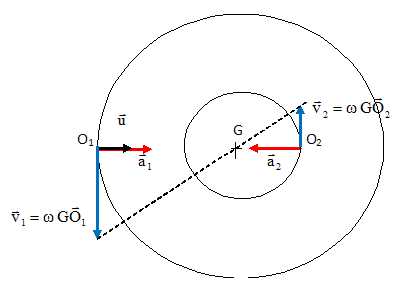
En déduire
que les rayons vecteurs GO1 et GO2 tournent
autour de G à la même vitesse angulaire
Les points O1 et O2 étant
constamment alignés, GO1 et GO2
tournent à la même vitesse angulaire w.
Dans ce qui suit, sauf mention particulière, seul ce type de mouvement
sera considéré.
|
| .
. |
|
|
Calculer
les rayons Ri. Établir
une relation entre D et la vitesse angulaire w. Sous
quel nom cette relation est-elle connue
?
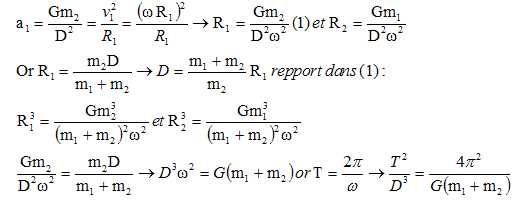
Cette
dernière relation exprime la 3è loi de Kepler.
|
.
Dans
cette question on ne fait pas d'hypothèse sur les trajectoires des
points matériels. On admet que 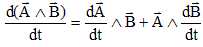
Montrer
que 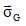 se
conserve aussi dans le cas général d'un point matériel O soumis à une
force passant par G puis dans le cas général d'un système de deux
points matériels en interaction gravitationnelle. se
conserve aussi dans le cas général d'un point matériel O soumis à une
force passant par G puis dans le cas général d'un système de deux
points matériels en interaction gravitationnelle.
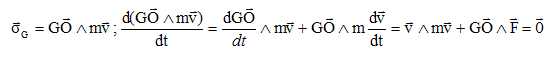
La force F et le vecteur GO étant colinéaires, le produit vectoriel de
ces deux vecteurs est nul.
Pour un systèmede 2 points matériels en interaction de gravitation, les
forces de gravitation sont colinéaires au vecteur O1O2
; la direction de ces forces passent par le centre d'inertie G.
Le calcul précédent s'applique : d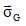 /dt étant nul,
alors /dt étant nul,
alors 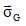 est constant. est constant.
Calculer
l'énergie cinétique Ec du
système des deux points Oi en
fonction de µ, D et w.
(On éliminera G en utilisant les résultats du mouvement circulaire).
Ec =½m1 v12
+½m2
v22 avec v1
= m2/(m1+m2)D
w
et v2
= m1/(m1+m2)D
w.
Ec =½m1 ( m2/(m1+m2)D
w)2+½m2(m1/(m1+m2)D
w)2.
Ec
=½m1m2/ ((m1+m2)D2w2
(m2/(m1+m2)+m1/(m1+m2)) =½µD2w2.
On définit
l'énergie potentielle d'interaction Ep entre les
deux points par les relations différentielles suivantes qui font
respectivement intervenir les accroissements infinitésimaux dEp,
d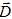 et dD des
grandeurs Ep, et dD des
grandeurs Ep, 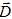 et D : et D :
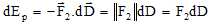
Par
convention Ep = 0 lorsque les deux points sont
infiniment éloignés.
Déterminer
Ep
en imaginant, par exemple, que le point matériel O2
est éloigné très lentement de O1 sous l'action
d'un opérateur qui lui applique à chaque instant une force Fop
infiniment proche de F2 (bien que très
légèrement supérieure) et qui, de ce fait, effectue un travail
élémentaire dW
= dEp lorsque la distance D s'accroît de dD.
dEp = Gm1m2dD/D2
; intégrer : Ep = -Gm1m2
/ D +Cste.
L'énergie potentielle est nulle lorsque D devient très grand, la
constante d'intégration est donc nulle.
De plus G = D3w2/(m1+m2)
; par suite : Ep
= -µ D2w2.
En déduire
l'énergie mécanique totale Em du
système considéré en fonction de D, w et µ.
Em =
Ec
+Ep =½µD2w2-µ D2w2 =-½µ D2w2 .
|
|
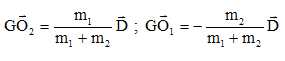
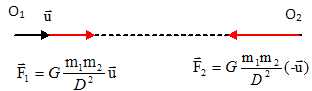
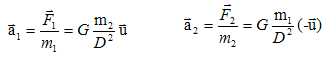

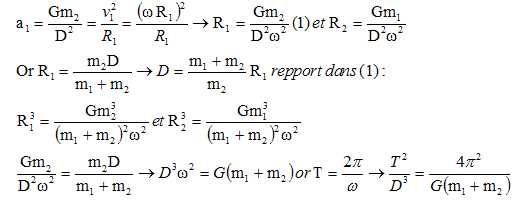
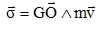 .
.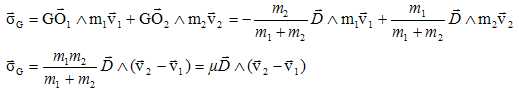
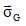
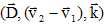
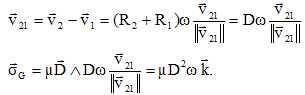
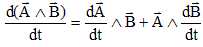
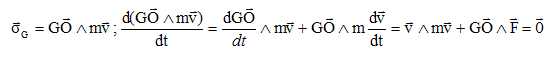
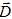 et dD des
grandeurs Ep,
et dD des
grandeurs Ep,