Oscillateur
mécanique, pendule, objectif photographique : concours audioprothésiste
Rennes 2007
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Oscillateur
mécanique horizontal.
On
étudie le comportement d'un ressort accroché à une potence en
suspendant différentes masses à l'extrémité libre E. Le zéro de la
règle correspond à la position de E à vide. On relève l'allongement du
ressort pour différentes masses.
m(kg)
|
0
|
0,2
|
0,4
|
0,5
|
0,7
|
1
|
DL(m)
|
0
|
0,05
|
0,10
|
0,125
|
0,175
|
0,249
|
DL / m
|
xxx
|
0,05
/0,2 =0,25
|
0,1/0,4=0,25
|
0,25
|
0,25
|
0,25
|
Déterminer la
relation entre DL et m.
DL / m =0,25 m kg-1.
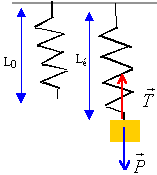
Représenter
sur un schéma les forces s'exerçant sur la masse m.
La masse m est soumise à son poids et une force de rappel exercée par
le ressort.
 Exprimer leur somme
à l'équilibre.
Exprimer leur somme
à l'équilibre.
A l'équilibre la somme vectorielle de ses deux forces est nulle.
En
déduire l'expression de la raideur k du resort. Calculer k. On
prendra g = 9,81 m s-2.
mg = kDL ; k = mg / DL =0,25*9,81 = 2,45 N m-1.
Le ressort précédent est utilisé pour réaliser un oscillateur élastique
horizontal. On néglige l'ensemble des frottements. On étudie le système
sur un axe horizontal. A l'équilibre, le ressort n'est pas déformé.
L'abscisse x du centre d'inertie du solide est nulle. A l'instant
choisi comme origine des temps, on écarte lla masse m et on la lâche
sans vitesse initiale.
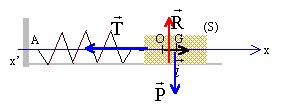
Faire
l'inventaire des forces extérieures appliquées sur le solide
immédiatement après le lâcher et les représenter.
Le système ( le solide )est soumis à son poids, à l'action du support
et à une force de rappel exercée par le ressort.
Appliquer
le théorème du centre d'inertie et déterminer l'équation différentielle
du mouvement de m.
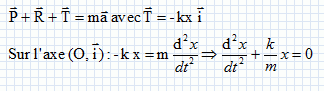
|
|
|
En déduire
l'expression de la constante w0
de cette équation ainsi que la période propre T0 en fonction
de k et m.
w02
= k/ m = 2p /T0 ; T0 = 2p(m/k)½.
On mesure la durée de 10
oscillations et on trouve 10,6 s. Calculer T0.
T0 =10,6 / 10 = 1,06 s.
|
.
|
|
Pendule simple.
Un pendule simple est constitué d'une petite
boule métallique de masse m = 800 g reliée à un fil de longueur L = 1
m. Il est lâché, fil tendu, avec un angle q0 = 70°.
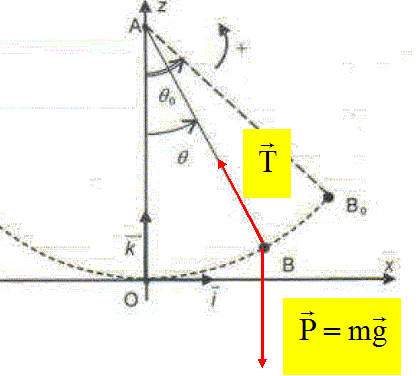
Calculer le travail
du poids entre la position B0 et la position O.
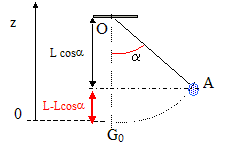
Le travail du poids est positif en
descente et vaut : mg L(1-cos q0)
=0,800*9,81(1-cos 70) =5,16 J.
En
déduire la vitesse de la boule en O.
La tension du fil,
perpendiculaire à la vitesse ne travaille pas.
Ecrire le théorème de l'énergie cinétique entre B0 et O.
½mv2-0 = travail du poids =5,16 J
v2 = 2*5,16 / 0,800 =12,9 ; v = 12,9½ ~3,6 m/s.
|
Objectif photographique.
Un objectif photographique est modélisé par une lentille mince
convergente de distance focale f ' =80 mm. On peut faire la mise au
point en déplaçant l'objectif par rapport à la pellicule.
Où faut-il placer la pellicule pour photographier un objet éloigné ?
L'image d'un objet éloigné se trouve dans le plan focal image de la
lentille convergente ; la pellicule sera placée dans ce plan.
Construire l'image d'un objet éloigné et calculer sa grandeur.
Cet objet est un arbre de10 m de haut situé à 300 m du lieu d'observation.
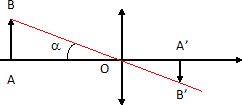
tan a = AB / OA =A'B' / f ' ; A'B' = AB f '/ OA =10*80 / 300 =2,7 mm.
|
| |
|