Plongée d'un
bathyscaphe ; fission de l'uranium 235 : concours audioprothésiste
Rennes 2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Plongée d'un
bathyscaphe.
Un
bathyscaph est constituée d'une lourde cabine pouvant accueillir 2 ou 3
personnes, suspendue à un flotteur rempli d'un liquide noté "L", moins
dense que l'eau, qui compense le poids. Pour plonger, le bathyscape
largue une partie du liquide L qu'il remplace par de l'eau de mer.
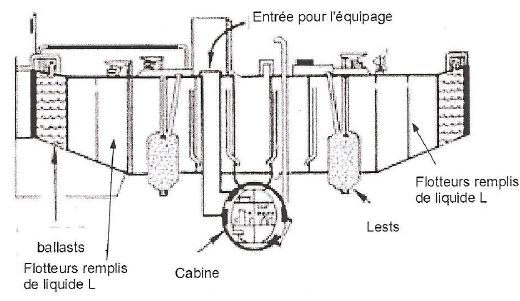
Masse totale du bathyscaphe : M = 200 t ( liquide L compris ) ;
volume total du bathyscaphe V = 194 m3 ; masse volumique de
l'eau de mer : re
=1,03 103 kg m-3 ; masse volumique du liquide L :
rL =0,66 103
kg m-3 ; g = 9,8 m s-2.
Le bathyscaphe est complétement immergé mais ne plonge pas encore.
Exprimer puis
calculer la poussée d'Archimède s'exerçant sur le bathyscaphe.
FA = re Vg =1,03 103 *194*9,8
=1,958 106 ~1,96 106 N.
Comparer la poussée
au poids et conclure.
P = Mg = 2,00 105 *9,8 =1,96 106 N.
Le poids et la poussée ont à peu près la même valeur. Le bathyscaphe
reste en équlibre.
Le
bathyscaphe remplace un volume V' = 2 m 3 de liquide L par le
même volume d'eau de mer.
La valeur de la
poussée d'Archimède varie-t-elle ? Expliquer.
Le volume du bathyscaphe immergé ne varie pas : en conséquence la
poussée d'Archimède reste inchangée.
Déterminer
l'expression littérale de la variation de masse DM du bathyscaphe. Faire l'application
numérique.
Masse de 2 m3 de liquide L : V'rL ; masse de 2 m3
d'eau de mer : V're
DM
=V'(re-rL) =2(1,03-0,66)103
=7,4 102 kg.
Expliquer pourquoi
le bathyscaphe se met à descendre.
L'équilibre
est rompu, le poids étant devenu supérieur à la poussée.
Calculer la nouvelle
masse M' du bathyscaphe.
M' = M + DM =200 +0,74 =
200,74 t = 2,0074 105 kg.
Faire
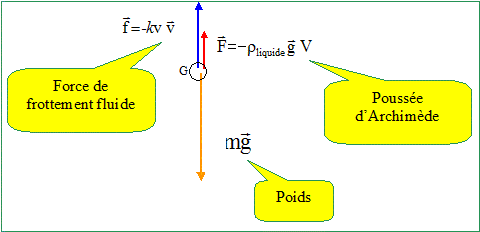
le bilan des forces exercées sur le bathyscaphe lors de la descente.
Représenter, sans échelle, ces forces sur un schéma.
|
|
|
On
suppose que la valeur de la force de frottement exercée par l'eau est
modélisée par la relation f = kv2 avec k =9,0 103
kg m-1.
Etablir l'équation différentielle du mouvement selon l'axe vertical
descendant.
La seconde loi
de Newton conduit à : M'g -kv2-reVg = M'dv/dt.
Le bathyscaphe atteint une vitesse limite. Donner l'expression
de cette vitesse puis la calculer.
M'g -kvlim2-reVg =0 ; vlim2= g(M'-reV) /k.
vlim= (g(M'-reV) /k)½
=(9,8(2,0074 105-1,03 103*194)/(9,0 103
))½=1,00 m/s.
Justifier l'unité de
k par analyse dimensionnelle.
k est une force divisée par le carré d'une vitesse ; une force est une
masse fois une acclération :
[k] =M L T-2 / (L T-1)2 =ML-1.
( kg m-1).
|
.
|
|
Propulsion
du sous-marin "le terrible".
Ce sous-marin utilise comme combustible de l'uranium enrichi en 23592U.
Masse d'un noyau 23592U
: m(U) =235,0439 u ; masse d'un noyau 9438Sr
: m(Sr) =93,9154 u ; masse d'un noyau 14054Xe
: m(Xe) =139,9252 u ; masse d'un neutron 10n :
m(n)=1,0087 u ;
1 u = 1,66 10-27 kg ; masse molaire 23592U
: M =235 g/mol.
Donner la structure
du noyau d'uranium 235 ?
92 protons et 235-92 = 143 neutrons.
Ces noyaux peuvent donner différentes fissions. La plus fréquente est
donnée par :
23592U+10n--->
14054Xe
+ 9438Sr
+ x10n.
Montrer
que x=2. Justifier .
Conservation du nombre de nucléons : 235+1 =140+94+x ; x = 2.
Conservation de la charge : 92 = 54+38 est bien vérifiée.
Montrer que
l'énergie libérée par la fission d'un noyau d'uranium 235 vaut Elib
= 2,91 10-11 J.
Dm= m(n) +m(Sr) +m(Xe) -m(U)
=1,0087+139,9252+93,9154-235,0439=-0,1946 u ou -0,1946*1,66 10-27
=-3,23 10-28 kg.
Elib =|Dm|c2
=3,23 10-28 (3,00 108)2=2,91
10-11 J.
On suppose pour simplifier que les énergies libérées par toutes les
réactions de fission sont approximativement égales à celle calculée.
Le réacteur fournit une puissance moyenne de 150 MW.
Calculer le nombre
de fissions par seconde.
150 106 J s-1 ; 150
106 /(2,91 10-11)
=5,16 1018 fissions par seconde.
En déduire la masse
d'uranium consommé en une seconde.
5,16 1018 *3,23 10-28 =1,67 10-9 kg.
Un tel sous marin est prévu pour naviguer pendant une durée de deux
mois.
Quelle
masse d'uranium 235 doit-il embarquer pour assurer son
approvisionnement énergétique pendant cette durée ?
1 mois = 2,6 106 s ; 2*2,6 106
*1,67 10-9 =8,7 10-3
kg.
|
|