Champ magnétique
d'une bobine plate, effet Doppler.
Concours kiné Berck 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Champ
magnétique d'une bobine
On
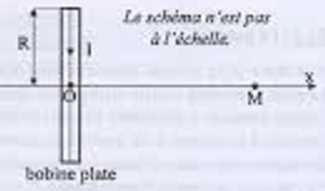
considère une bobine plate circulaire de centre O, comportant N = 150
spires, de rayon R = 20,0 cm et parcourue par un courant d'intensité I
= 1,5 A. On mesure à l'aide d'un teslamètre la valeur du champ
magnétique en un point M situé sur l'axe de la bobine. La position du
point M est repérée par l'abscisse x = OM. Au point M considéré, on
mesure B = 446 µT.
On propose ci-dessous différentes expressions pour calculer la valeur
du champ magnétique en M.
On donne µ0 = 4 p
10-7 SI.
Quelle expression
est exacte ?
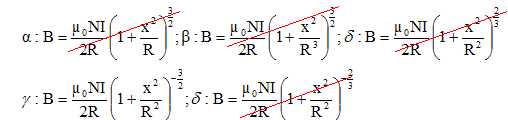
Calculer la valeur de x (
en cm).
µ0NI/(2R) =4*3,14 10-7*150*1,5
/(2*0,20) =7,069 10-4 ;
2RB / (µ0NI)
=446 10-6 /(7,069
10-4)=0,631.
1+x2/R2 = 0,631-2/3 =1,36.
x2/R2
=0,36 ; x/R = 0,6 ; x = 0,6*0,20 =0,12 m = 12 cm.
Effet Doppler.
Une voiture téléguidée s'éloigne suivant une trajectoire rectiligne à
vitesse constante V d'un émetteur et d'un récepteur d'ultrasons. Le
récepteur est situé juste à côté de l'émetteur. L'émetteur E envoie une
onde ultrasonore périodique de fréquence fE. L'onde se
réfléchit sur la voiture et elle est reçue par le récepteur R. La
fréquence du signal reçu est notée fR. La direction de
propagation des signaux émis et reçus est confondue avec la direction
de déplacement de la voiture. Un système d'acquisition permet
d'analyser les signaux émis et reçus..

|
|
|
Dans les conditions de l'expérience, la célérité
des ultrasons vaut c = 343 m/s.
Déterminer
les fréquences fE et fR en justifiant.
Le véhicule s'éloigne de l'émetteur : le son reçu est plus grave que le
son émis. fR <fE.
Ajoutons que l'amplitude du signal reçu et inférieure à celle du signal
émis.
fE = 40,0 kHz et fR = 39,278 kHz.
Etablir
l'expression de la vitesse V en fonction de fE, fR et c.
On note T la période des ultrasons émis, T' la période du son reçu et d
la distance entre la voiture et l'émetteur à la date t1,
instant de l'émission.
Le
son parcourt la distance d à la célérité c : t' = d /c + t1.
La voiture
parcourt la distance vT en T seconde.
Distance entre la source S et E au bout de T seconde : d2 =d+vT
Le
son parcourt la distance d2 à la célérité c : t" = d2 /c + t1+
T = (d+vT) / c+
t1+
T
T ' = t"-t' =(d+vT) / c+
t1+
T-( d /c + t1)
T ' =T +vT / c = T
( 1+v/c).
f ' =fE /(1+v/c).
Il faut tenir compte du double effet Doppler après réflexion sur la voiture ( le récepteur est fixé sur le récepteur).
En conséquence :
fR =fE /(1+v/c)2~fE (1-2v/c) ; v/c étant petit devant 1.
fE
=fR(1+v/c) ; fR
/ fE=1-2v/c ;
v=½c (1-fE
/ fR).
Calculer
v en km/h.
v = 0,5* 343(1-39,278/40 ) =3,1 m/s ou 3,1*3,6 =11,1 km/h.
|
.
|
|
La
direction du déplacement de la voiture fait maintenant un angle a = 17,0° avec la direction de
propagation des ultrasons et la voiture se déplace vers l'émetteur et
le récepteur d'ultrasons. La valeur de la vitesse n'est pas modifiée
par rapport à la question précédente.

La fréquence du signal reçu est notée fR'. On propose
ci-dessous différentes expressions pour calculer fR'.
Indiquer
l'expression correcte en justifiant.
(a) : fR'
= fE(1-2V cos a /
c) ; (b) : fR' = fE(1-V cos a / c) ; (c) : fR'
= fE(1+V cos a /
c) ; (d) : fR' = fE(1+2V cos a / c).
(a) et (b) sont fausses : la voiture s'approche de l'émetteur, la
fréquence du son reçu est plus grande.
La
projection de la vitesse v sur la direction de propagation des
ultrasons conduit à v cos a.
Tenir compte du double effet Doppler après réflexion de l'onde sur la voiture.
fR' = fE(1+2V
cos a / c).
Calculer
la valeur de la différence de fréquence en Hz.
fR'-fE =2fEV cos a / c =2*40 103*3,1 cos
17,0 / 343 =691 Hz.
|
|
|