Couleurs des
objets, numérisation d'un signal. Concours audioprothésiste Bordeaux
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Une
image numérique est généralemet codée en RVB 24 bits. Cela signifie que
le nombre de couleurs possibles s'élève à : 24 ; 576 ; 16 777 216 ; 16 752 364
; 192.
224
= 256*256*256 = 16 777 216.
Concernant le
mélange des couleurs, une seule des propositions suivantes est juste.
Laquelle ?
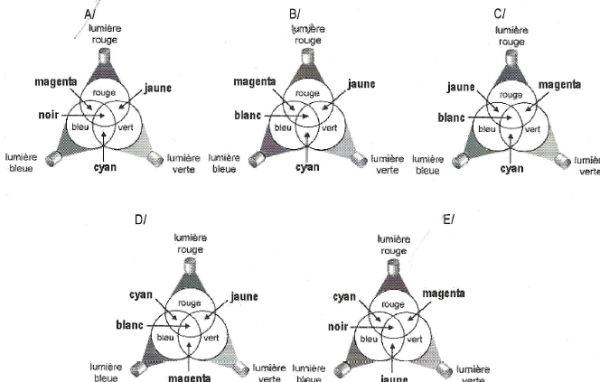
En synthèse additive, la superposition du
rouge, vert et bleu donne le blanc. Le rouge superposé au vert donne le
jaune ; le vert et le bleu donnent le cyan ; le bleu et le rouge
donnent le magenta. B
est exact.
On interpose sur un faisceau
lumineux de lumière blanche différents filtres afin d'obtenir la
couleur rouge à l'écran. Une seule des propositions suivantes est
juste. Laquelle ?
On superpose
un filtre jaune et un filtre magenta ; on supperpose un filtre
bleu et un filtre vert ;
on supperpose un filtre cyan et
un filtre magenta ;
on supperpose un filtre cyan et
un filtre jaune ;
on superpose un filtre vert et un filtre magenta.
Il faut éliminer le vert
et le bleu. Un filtre magenta laisse passer le magenta ( rouge et bleu
) mais abosrbe le vert ; un filtre jaune laisse passer le jaune ( rouge
et vert ) et absorbe le bleu.
Concernant le mélange des couleurs, une
seule des propositions suivantes est juste. Laquelle ? E.
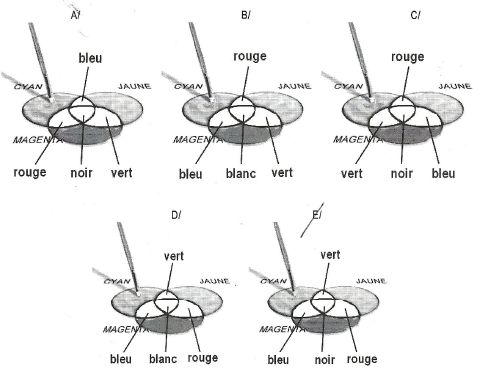
En synthèse soustractive,
la superposition du cyan, magenta et jaune donne le noir ; le jaune est
un mélange de vert et de rouge ; le cyan est un mélange de vert et de
bleu.
Au niveau du codage RVB, indiquer les couleurs correspondant aus=x
différents codes ci-dessous :
Rouge
|
0
|
128
|
255
|
255
|
0
|
0
|
Vert
|
0
|
128
|
255
|
255
|
255
|
255
|
Bleu
|
0
|
128
|
255
|
0
|
0
|
255
|
couleur
|
noir
|
gris
|
blanc
|
jaune
|
vert
|
cyan
|
Noir, gris, blanc, jaune, vert,
cyan ; noir, gris, blanc, jaune, vert, magenta ;
noir, gris, blanc, cyan, vert, magenta ; blanc, gris, noir, jaune,
vert, cyan ;
blanc, gris, noir, cyan, vert, magenta.
|
|
|
Déterminer la fréquence d'échantilonnage du signal numérisé suivant :
(400 Hz ; 5 kHz ; 10 kHz ; 5 MHz ; 4 kHz ).
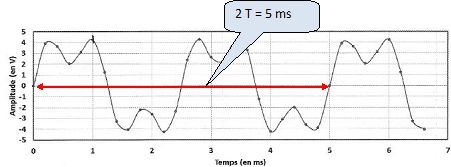
13 points de mesure par période ; chaque mesure est effectuée en 2,5 10-3/13 ~1,92 10-4 s ; féquence d'échantillonnage fE =1/(1,92 10-4 ) ~ 5 kHz.
Déterminer la fréquence fondamentale du signal. ( 400 Hz ; 5 kHz ; 10 kHz ; 5 Mhz ; 4 kHz
).
f = 1/T = 1/(2,5 10-3) = 400 Hz.
On considère un matériau transparent d'indice de réfraction n= 1,8.
Quelle est la vitesse de propagation de la lumière dans ce matériau ? (
183 000 km/s ; 167 000 km/s ; 540 000 km/s ; 300 000 km/s ; 142 000 km/s ).
c / n = 3,0 108 / 1,8 = 1,67 108 m/s = 1,67 105 km/s.
|
|
|
On définit le coefficient d'atténuation linéique a par a = |10/L log( PS / PE)| où PS et PE
représentent les puissances de sortie et d'entrée et L la longueur de
la fibre. Pour une fibre de longueur 100 km caractérisée par le graphe
suivant, calculer le rapport PS / PE maximum dans le domaine de longueur d'onde considéré.
( 100 ; 10-200 ; 10200 ; 0,001 ; 0,01 ).
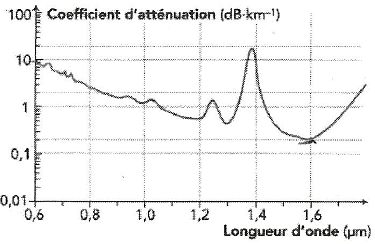
Le coefficient d'atténuation linéique ( 0,2 dB / km) est minimal pour une longueur d'onde de 1,6 µm.
Atténuation au bout de 100 km : -0,2*100 = -20 dB.
-20= 10 log( PS / PE) ; log( PS / PE) =-2 ; PS / PE =0,01.
Si on injecte un faisceau de longueur d'onde 700 nm et de puissance 1 W
en entrée d'une fibre de 1,2 km dont les caractéristiques sont les
suivantes, calculer la puissance de sortie.
(973 mW ; 10-12 W ; 871 mW ; 10-60 W ; 0,01 W ).
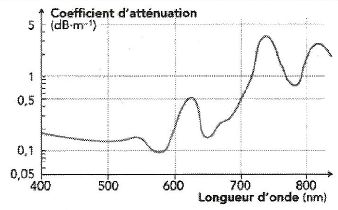
Le coefficient d'atténuation linéique est égal à 0,5 dB / km pour une longueur d'onde de 700 nm.
Atténuation au bout de 1,2 km : -0,5*1,2 = -0,6 dB.
-0,6= 10 log( PS / PE) ; log( PS / PE) =-0,06 ; PS / PE =0,871.
Afin de numériser un signal sonore, on utilise un microphone relié à
une carte d'acquisition de résolution 8 bits, utilisée sur le calibre
[-1 V ; + 1 V ]. On enregistre pendant une durée dt = 100 ms et de la
manière la plus fidèle possible avec cette carte, un son de fréquence
500 Hz. Quelle est la résolution en tension ?
0,00078 V ; 0,0078 V ; 0,078 V ; 0,78 V ; 7,8 V.
2 / 28 = 7,8 10-3 V.
|
|
|